基于EMD 分解在电火花数据分析的应用
2017-1-9 来源:合肥工业大学电气与自动化工程学院 作者:刘春 杜雲
摘要: 经验模态分解( empirical mode dccomposition,EMD) 是处理非平稳、非线性信号一种有效的新方法。运用EMD 分解法将脉冲典型负荷—电火花信号中本征模态函数( intrinsic mode function,IMF) 分量逐级分离出来,得到原信号的多尺度振荡特性; 分析各个分量与原序列的显著性检验和相关系数以及各个分量自身的周期性。用IMF 分量和趋势项合成原序列并作误差分析,得到信号的总误差率通过理论计算为4. 3%。利用bior4. 4 和db2 两种小波基在3 层分解系数基础上对电火花数据展开小波包变换。最后借助MATLAB 平台对EMD 和小波包分解方法进行仿真并做理论对比分析。结果表明,EMD 分解法在提取机床运行放电特性及不同工况下信号更具优越性和有效性,提取结果更能满足实际工程应用需求。
关键词: 脉冲电能; 电火花; 经验模态分解; 小波包变换
1.引言
近几年,采用电火花加工技术在加工复杂型面、深槽和窄缝等应用中所占比重越来越大。脉冲电能负荷不同的工况应用条件,造成脉冲电能质量扰动因素种类繁多。放电状态又是对电火花加工过程实施准确控制的主要依据,直接决定了加工质量、加工效率和电极损耗等工艺指标的优劣[1]。然而,传统电火花加工工艺效果受多种工艺参数( 尤其是电参数) 影响,加工工艺效果难以实现自动化生产。因此,研究电火花加工电参数的优化选择,对工艺效果控制及自动化加工的实现具有重要意义[2]。从而,进一步提高加工效率、精度及加工过程的稳定性。
为了更好地提高电火花加工表面质量,国内外学者对其加工表面微观形貌做了大量的研究。研究比较多的有高斯滤波和小波滤波。Raja 等人[3]将快速傅立叶变换引入高斯滤波。Hara 等人[4]用两阶Butterworth 高通滤波器模拟高斯滤波的转换特性,提高了运算速度却导致了相移,降低了运算精度。但是,傅里叶变换由于信号的复杂性导致频率变化剧烈,且它的窗口的大小固定不变,导致分辨率固定。针对该缺陷,陈庆虎等人[5] 选择Shannon 小波,采用Mallat 快速分解算法,提出基于小波分析的理论和方法,小波滤波产生的三维基准面,光滑自然,能精确地把表面粗糙度和其他表面结构成份分离。小波变换继承了窗口变换的局部化思想并改进了傅里叶变换的弊端,是一种自适应的时频分析方法; 但是小波变换在小波基选择、小波基函数固定、阀值确定对于不同信号很难做出最佳选择。为彻底解决传统分析方法对电火花信号的的局限性[6-8],将不需要信号先验知识和无需定义基函数的经验模态分解( EMD) 法引入到电火花信号分析中,把电火花信号内在的放电特性通过本征模态函数( IMF) 分量展现出来。
本文运用EMD 分解法对机床放电特性的电火花数据进行逐级分解,并综合已有的小波分析方法作对比,重点分析了IMF 分量与原数据显著性检验和相关系数,采用自相关函数求功率谱寻找每个分量周期值; 将IMF 分量和趋势分量逆变换叠加还原数据,对比原数据做误差分析并考量原序列的主成分。本文最后部分,将实测电火花的电流信号分段做EMD 生产实际分析。EMD 分解法是分析电火花机床的一种有效方法,IMF 分量可体现电火花机床的内在多尺度振荡特性—放电特性,为电火花机床的运行状态进行实时监控提供指导。
2.理论基础
2.1 IMF
EMD 将原序列分解成有限个IMF 分量,并且分量的瞬时频率各不相同; 使得IMF 分量有物理意义的必要定义是: 函数关于零均值线是局部对称,并且穿零点和极值点的数目是一样的。鉴于此,给出本征模态函数的确切定义: 1) 在信号序列里,极值点的数目与穿零点的数目必须相等或者最多相差一个; 2) 由局部极大值所构成的包络线以及由局部极小值所构成的包络线的平均值为零。对于非平稳信号而言,定义一要对“局部平均”一段一段求,然而局部时间长度很难知道; 定义二是一个新思路,用上下包络线的局部平均值为零来表征局部对称性,巧妙的避开了局部时间尺度的问题。
ZMF 表征了信号序列内在的,固有的振荡状态; “状态”一词,泛指涨落、起伏、变化,不一定具有周期性; 但是如果一个振荡经过显著性检验具有周期性,则称之为周期性振荡。
2.2 经验模态函数分量IMF 的筛选过程
EMD 的关键性问题就是如何把一个非平稳非线性的信号分解成有限个IMF 分量和一个趋势项。采用合适的筛选方法,筛选出符合定义的IMF分量[9-11]。给定原信号,把所有局部极大值用3 阶样条曲线连接起来得到上包络线,运用同样方法把局部极小值连接起来得到下包络线; 上下包络线分别涵盖信号全部极大值和极小值; 再取上下包络线的均值线m1,将原序列 X( t) 与均值线 m1 ( t) 做差得到:

上述步骤只是筛选过程的第1 步,得到的h1 ( t) 不符合对 IMF 的要求,原因是: 1) 经 3 次样条连接后把某些极大值夸大了,出现了一些过高峰和过低谷; 2) 信号复杂,在峰或谷上有很多骑行波,就是零均值线的上下方起伏的弯曲,骑行波不满足IMF 要求且一次筛选不能完全消除骑行波;3) 非线性信号来说,包络的均值线和真正的局部平均线不一样,某些非对称波形依然存在,一次筛选无法消除非对称波形。鉴于上述原因,必须进行重复多次筛选。
进行第2 次筛选时,把h1 ( t) 当作“原始序列”,重复第1 筛选步骤h1 ( t) - m11 ( t) = h11 ( t) ,

SD 的门限值要根据具体的信号来设定,门限的参考数值可取0. 2 ~ 0. 3。前后2 次筛选结果的SD 值达到预先设定值,则停止筛选过程。第1 步筛选结果得到的C1应是信号的特征时间尺度最小的高频IMF 分量。接下来,就把C1从原序列中分离出去,得到一个剩余序列r1 ( t) :

2.3 小波包理论及滤波算法过程
小波分析的思想是用一簇函数去表示或逼近信号,这簇函数称为小波函数系。在小波包分解过程中,随分解层数增加数据点成倍减半[12]。若电火花数据长度为2N ( 本文实测的电火花数据长度N = 10 ) ,分解L 次,则每个频段数据长度变为2N - L。利用小波包可以将信号按任意时频分辨率分解,将信号正交分解到相应的频段。并根据先验知识,保留分解序列中任意一个或几个频段序列进行重构,重构信号长度仍为2N。小波包滤波算法的实现过程:



3.仿真结果及分析
本文以一组实测机床放电电流全过程电火花信号作为扰动信号样本进行EMD 分解,得到5 个IMF 分量和一起趋势分量R 如图1 所示。根据实际经验门限值通常去0. 2 ~ 0. 3。本次实验的EMD门限值取0. 2。
3.1 IMF 分量的周期性分析
为了分析IMF 分量的周期性特征,本文采用基于自相关函数法求本征模态函数的功率谱进而寻找周期性[13-14]。在MATLAB 中对各个分量进行功率谱分析,将获得的最大谱对应的周期如表1所示。

图1 本征模态函数( IMF 分量和趋势分量)
表1 自相关函数求功率谱寻找电流时间序列周期

表1 结果表明: 本组数据EMD 分解后的每个细致分量IMF 都表现出一定的周期性。在最大落后步长M = 10,30,50 不同情况下,IMF 分量表现出不同的周期性,这是因为最大落后步长越小导致时间序列越短,因而在基于自相关函数的功率谱最大谱上面对应的周期越小; 但在低频分量IMF4 和IMF5,对于最大落后步长对其周期性的影响减弱。深入分析IMF2 和IMF3 分量周期在不同M 值的情况下周期跳跃性较大,结合图1 中IMF2 和IMF3的幅值是其余分量的10 和100 倍,假定IMF2 和IMF3 可能是原始信号的主成分。
3.2 IMF 分量的显著性和相关系数分析
为了更加准确地表征每个IMF 分量与原电流序列统有无显著性差别和相关性程度[15],在MATLAB 中对每个分量进行显著性检验和相关系数测定,结果如表2 所示。
表2 IMF 分量与原电流时间序列的显著性检验和相关系数

表2 结果表明: 在每个IMF 分量对原序列做显著性检验时,发现显著性水平H 值都为0,说明所有的IMF 分量都通过了的显著性检验,结合上述的周期性分析,理论上认为本组数据是周期性振荡的。然而,每个分量的显著性概率却不相同,表明每个分量对于原序列的影响有大小之分; 结合相关系数的数据特点,有理由证实IMF2 和IMF3 是原序列的主成分,并且其携带了原信号大部分信息。
3.3 IMF 分量的逆变换和误差分析



表3 误差分析
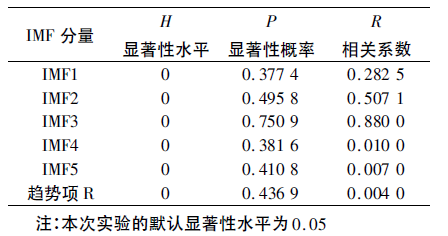
图2 和表3 联合结果表明: IMF2 + IMF3 分量虽然有误差但在可接受范围内,能较好好拟合原电流时间序列,说明IMF2 和IMF3 是原信号的主要分量,实验验证了前面理论分析的正确性。当所有的IMF 分量相加后得到的信号与原信号的总误差率通过理论计算为4. 3%,说明EMD 分解法不仅可以表现信号的本质性质,同时不会减少信号的完备性; 也实现了EMD 分解法的逆变换。
4.应用分析
为了更清晰地分析EMD 分解法的有效性,将同时利用小波分析和EMD 分解法对电火花数据进行分析。
4.1 小波包的电火花应用分析
以采样时间为20 个工频周期,采样点N =1 000,采样频率fs = 1 kHz,取信号额定频率为50 Hz。本文小波基函数分解是在3 层分解系数基础上展开。利用MATLAB 的强大信号处理功能,实现上述过程,结果如图3 和4 所示。


图3 电火花50 A 信号bior4. 4 小波分解
4.2 EMD 分解的电火花应用分析
利用EMD 分解法对实测的机床电流放电过程进行分段分割分析,并分析每个分量的频谱特性,找到各分量的物理意义,从而更好地理解机床电流放电的内部过程。EMD 门限值取0. 2,利用MATLAB 绘制结果如图5 和6 所示。


图4 电火花50 A 信号db2 小波分解
4.3 小结
从图3 和4 可以看到: db2 小波在对电火花50A 信号的滤波效果不如bior4. 4 好,然而在频率保持方面db2 小波变现的更为出色。bior4. 4 小波在不同阀值对电火花去噪影响情况下,默认阀值的波形没有调节阀值的好,而默认阀值的却滤除了其余谐波的影响。图5 和6 结果表明: 对于不同的机床运行过程,从IMF1 分量到IMF5 分量,都可以逐级清晰地分解出原电流时间序列不同阶段的高频和低频分量。结合图1 的趋势项以及上一节的理论分析,可以看出经过EMD 分解后的电流序列个分量随着时间变化呈现一些周期性变化。对于各分量可以很容易看出: IMF1 包络了信号的5 次、7 次和9 次谐波含量,IMF2 包络了号的3 次、5 次和7 次谐波含量; IMF3 包络了信号的基波含量; IMF4 和IMF5 包络了信号的低频分量。


图5 未放电电流时间序列EMD 分解和频谱


图6 放电过程中电流时间序列EMD 分解和频谱
对实测信号的试验表明,采用需选择合适的小波包算法,并给定合适的阈值才能分析出点火花信号的部分特性。与小波分析法相比,一方面,EMD分解不仅无需信号的先验知识和固定的基函数; 且可获得电火花信号的内在放电特性。另一方面,EMD 分解法在提取机床运行的早期信号、微弱信号和突变信号等各方面信号更具优越性和高效性,提取结果更能满足实际工程应用需求。
5.结论
EMD 分解法是一种新的序列分解方法,本文以一组机床放电电流特性数据为基础,借助MATLAB 平台对EMD 分解过程和其分量进行细致的理论和实验对比论证,得出其在保证信号完备性的基础上,具备处理间歇性、非平稳和非线性序列的良好效果,同时具有直观、简洁和适应性强等优点。因此EMD 分解方法特别适用于电火花这类非平稳与非线性信号的处理给研究电火花加工工艺参数和加工工艺效果之间的关系的研究人员提供了一种新思路。从而实现电火花加工向高效、高精、自动化方向发展。EMD 分解法刚刚起步,研究领域众多,本文缺乏将EMD 分解法与经典信号分解法的对比性分析,将在以后的研究中改进。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息




