摘 要:为改善高速走丝电火花线切割的加工质量和效率,建立电参数与工艺指标之间的最优化模型,通过非线性规划求得二者之间的多目标函数关系,并利用Matlab对此模型进行最优化求解,结果为合理选择高速走丝线切割的工艺参数提供了依据。
关键词:电火花线切割;电参数;工艺
0 引言
电火花线切割是利用电极丝与工件之间的火花放电产生局部高温蚀除材料以实现切割加工,其具有控制方式较为简单、加工精度高等特点,广泛应用于复杂型面或超硬材料加工等领域。由于高速走丝电火花线切割加工是一个复杂不稳定且受多种因素影响的过程[1],与低速走丝线切割相比,在加工的可靠性、稳定性方面存在较大差距,故合理选择电参数对保证加工质量、提高加工效率具有重要作用。因此,如何合理选择加工电参数,以提高加工精度和效率,成为高速走丝电火花线切割加工中亟待解决的问题[2]。
在对电火花线切割电参数的分析研究中,国外J.Larkiola等专家曾提出应用神经网络方法优化工艺参数[3],但是若试验的影响因子较多,则试验次数很多且计算过程复杂,而且神经网络算法也存在收敛速度较慢等问题。由于高速走丝线切割工艺本身属于较复杂的多输入、多输出的非线性系统,本文将采用非线性多目标规划方法建立其工艺模型,实现加工电参数的优选。
1 、电参数对线切割加工的影响
对工艺指标影响较大的参数有脉宽ON、脉间OFF、峰值电流IP、伺服电压SV。实践证明,脉冲电源的电参数对切削速度和表面粗糙度影响可近似用公式(1)表示:
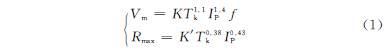
式中,K 为切割速度工艺常数;K′为粗糙度工艺常数;Tk为脉冲宽度(μs);IP为脉冲峰值电流(A);f 为放电频率(Hz/s)。由此可以看出,脉冲宽度、脉冲间隔和峰值电流等电参数对加工工艺指标影响较大。在对高速走丝线切割加工电参数的优选中,首先建立加工参数与工艺指标之间的工艺模型;然后在此基础上构造目标函
数,并根据加工要求确定参数的约束条件;最后采用优化工具对目标函数求解,以获得电参数优化及组合。线切割加工电参数各变量可分别用xi(i=1,2,3,4)表示,而将切割速度Vm和表面粗糙度Ra作为因变量,分别用μ(x)和v(x)表示,故工艺参数与目标函数之间的非线性关系可用公式(2)来表示:
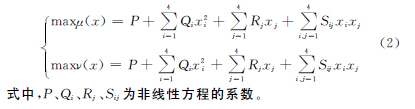
在电参数优化时,为了确定各自的目标函数,可得切割速度μ(x)与表面粗糙度v(x)目标函数分别为:
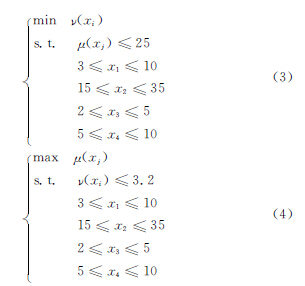
在对该问题进行优化时,是通过给定自变量的初始值进行迭代求解。可利用Matlab 中约束非线性最优化问题的fmincon函数,其调用方法为:[x,fval]=fmincon(fun,x0,A,
b,Aeq,beq,lb,ub,nonlcon)。工艺模型约束条件是Aeq·x=beq和A·x≤b,定义设计变量xi的上下界为lb 和ub,使得ub≥xi≥lb,在nonlcon参数中提供了非线性不等式c(x)≤0或等式约束条件ceq(x)=0。将公式(3)和公式(4)编制转化成M文件,作为非线性最小值优化的目标函数,给定向量xi作为问题迭代的初值,利用fmincon函数进行求解。
2 、电参数的求解优选
优选求解电参数目的是在保证高速走丝线切割加工质量的条件下,尽可能提高加工效率,即在满足工艺要求表面粗糙度的前提下使切割速度最大化。根据以上分析可知,电参数的优选属于有约束的非线性最优化问题。
课题的试验平台是北京阿奇夏米尔公司的ACTSPARKFW 型高速走丝线切割机床,试验采用的电极丝为0.20mm钼丝,选取YG6硬质合金钢作为试验材料,得到如表1所示的9组试验数据,将其作为建立多项式模型的样本数据。
表1 YG6钢的试验结果
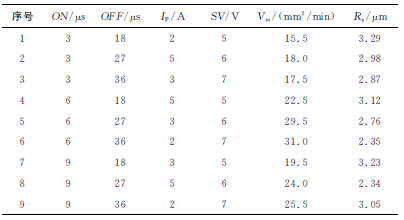

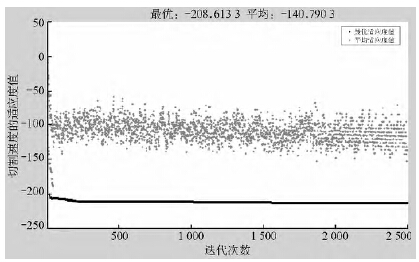
图1 切割速度最大值的求解
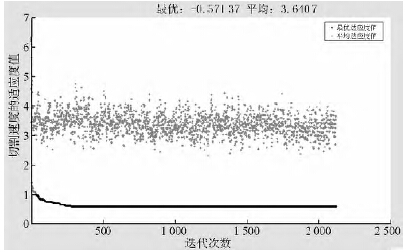
图2 粗糙度最小值的求解
因此,根据试验数据和优化模型结果进行线切割工艺参数的优化,表2为所得到的工艺参数优化方案。
表2 工艺参数优化方案

用优化得到的电参数进行实际电火花线切割试验,设置切割速度为25.0mm2/min,测得工件表面粗糙度为2.5μm,实际结果与本模型研究结果基本一致。
3 、结语
在高速走丝电火花线切割中,为改善加工精度并提高效率,本文首先建立了工艺电参数与工艺指标之间的非线性模型,然后通过试验方法获取迭代数据,其次利用Matlab工具对多目标函数进行求解,最后实现工艺电参数的优化和选择。本文研究结果为合理选择电火花线切割的电参数提供了参考和指导。
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com




