无偏差最小二乘法伺服控制系统参数辨识
2018-4-18 来源:合肥工业大学 作者:吴路路 韩江 田晓青 夏链
摘要:为准确辨识伺服控制系统参数,针对高性能运动控制算法的要求,在分析典型伺服控制系统结构模型基础上,基于“库仑摩擦+黏性摩擦”模型,设计了无偏差最小二乘方法,研究其在“工控机+运动控制卡”数控系统平台上的实现方法。实时采集电机角速度数据,利用设计的方法估算伺服系统转动惯量、黏性摩擦和库仑转矩,通过角速度重构,对比理论计算和实际测量角速度,验证参数辨识的有效性和准确性。理论分析和实验结果表明,所设计的参数辨识方法能够准确辨识系统参数。
关键词:伺服控制;无偏差最小二乘法;角速度重构;参数辨识
0、引言
设计高性能的伺服驱动控制系统,需要准确辨识执行机构的动力学参数。起初,控制系统都是基于偏差调节的反馈控制方式,为了降低运动轨迹的轮廓误差,要求各运动轴有匹配的闭环动态响应。随后,在传统反馈控制器的基础上,人们又提出前馈控制算法,即在控制器中引入了预估前馈数据。Tomizuka提出了一种零相位误差前馈控制器(ZPETC),通过在前馈控制器中输入零点来补偿闭环系统的不稳定零点,增加控制系统的带宽,提高伺服系统的跟踪精度。然而,对于ZPETC控制算法而言,如果想要设计具有较强鲁棒性的控制器,需要准确获取反馈系统的模型参数。
Ramesh等指出,如果控制系统参数与实际控制对象的参数不匹配,则使用前馈控制器反而会降低系统的控制精度,即使采用最小方差(generalised minimum variance)和极点配置方法设计系统控制器,如果想获得较好的控制性能也需精确知晓控制对象的参数。从工业上广泛使用的 P、PI、PID 控制器,到较为复杂的 ZPETC 控制器,再到更复杂的集成控制器,虽然各种控制算法都有一定的抗干扰能力,但对于突变的干扰来说,这些控制算法都需要一定的时间来消除突变干扰的影响。在圆弧插补的过象限处和线性轮廓拐角处,运动轴方向改变,摩擦力方向会随之发生突变,由于无法及时消除摩擦力的影响,该位置的精度会显著降低。解决这一问题的方式就是利用已知的信息(如插补的参考位置、速度),提前预估即将产生的干扰情况,通过前馈补偿的方式来消除突变干扰对系统运动精度的影响。然而,对于这种提前补偿的方式,需要预先获取突变干扰的特征。就进给系统中因运动方向改变而发生突变的摩擦干扰而言,需要提前掌握摩擦的特征才能进行补偿。
本文通过最小二乘法辨识进给驱动系统的动力学模型参数和摩擦干扰的特征参数,进给系统模型采用典型模 型,摩擦干 扰 模型采用 “库仑摩擦+黏性摩擦”模型。模型辨识实验在基于“工控机+运动控制卡+伺服电机”的运动控制平台上实现,通过重构电机运行速度,验证模型辨识的有效性。
1、伺服控制系统建模
伺服控制系统模型采用在实际应用中广泛使用的惯量阻尼模型,摩擦模型则采用“库仑摩擦+黏性摩擦”的结构。摩擦是影响进给系统控制精度的主要干扰因素,因此本文主要考虑摩擦因素,忽略测量噪声、量化误差等次要因素对模型参数的影响。
1.1 伺服系统模型
图1所示的进给驱动系统模型在伺服控制系统中广泛使用,系统中等效转动惯量为、黏性摩擦因数为B。u是输入的电压控制信号,由于伺服驱动系统的电流环带宽在几千赫兹以上,远高于系统的采样频率,因此电流环可简化成一个比例放大环节,比例系数为 Ka。经过驱动器的放大作用,在电机电枢中产生电流i,电机转动形成驱动转矩 Tm,电机的转矩常数为 Kt。 除了电机产生的驱动转矩 Tm外,导轨、丝杠、轴承上的摩擦力会在电机轴上产生干扰转 矩 Tf,驱 动 转 矩Tm 和干扰转矩Tf共同作用驱动电机轴转动。转动角速度为ω,电机轴连接导程为rg的滚珠丝杠副,经由丝杠将角速度转化为伺服系统的直线运动速度,直线运动速度为x·,经过一个积分环节得到伺服轴的位置x。
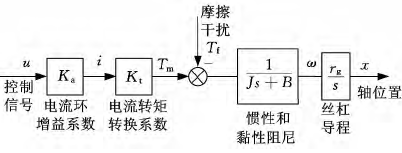
图1 伺服控制系统模型


1.2 摩擦模型
文献中对各种摩擦模型做了详细的阐述,“库仑摩擦 + 黏性摩擦”模型能够较准确地反映摩擦特性,相比其他摩擦模型而言结构简单,用较少的参数体现摩擦的特征,在工程中得到较广泛的使用。
文献从工程实用角度采用图2所示的模型,很好地补偿了摩擦的影响,摩擦转矩Tf与轴转速ω在一定程度上成线性关系。
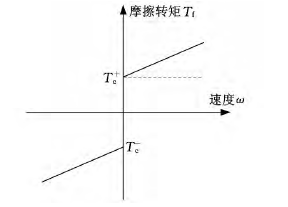
图2 摩擦模型
当驱动转矩小于库仑摩擦转矩Tc时,伺服系统运动轴处于停止状态,当轴运动后,随着角速度值增加,摩擦转矩成现线性比例增长,直线的斜率为进给驱动系统的黏性摩擦因数 B,当运动方向发生改变时摩擦转矩发生突变。摩擦转矩与角速度的关系如下公式所示:

2、系统参数辨识
利用图1所示的伺服系统模型和图2所示的摩擦模型,在一个简化的伺服系统上进行参数辨识实验。系统辨识采用两种方式:简单最小二乘法和无偏差最小二乘法。简单最小二乘法忽略库仑摩擦的影响,默认 Tc=0,实际辨识过程中只需估算转动惯量和黏性摩擦因数值;无偏差最小二乘法考虑摩擦干扰的影响,需要估算惯量、黏性摩擦因数和库仑摩擦值。
2.1 简单最小二乘法系统参数辨识
采用简单最小二乘法忽略运动方向改变时的摩擦突变的影响,认为 Tc=0。
根据式(3),如果

2.2 无偏差最小二乘法系统参数辨识
在实际工作过程中,由于干扰的存在可能会使得估算值出现较大偏差,故需要考虑干扰对估算值的影响,此时式(3)写成如下形式:

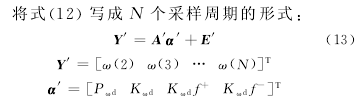

3、参数辨识实验
通过两种方法辨识伺服控制系统的转动惯量和黏性阻尼系数,与平台的实际转动惯量对比,验证无偏差方法的准确性;然后将两种方法辨识的结果分别代入到伺服系统模型中,根据输入指令计算系统的理论输出速度,并分别与实际采集的速度作对比,分析两种方法的速度偏差,验证无偏差方法的有效性。
3.1 实验平台
伺服系统参数辨识实验是在基于“工控机+运动控制卡+伺服电机”的平台上进行的,如图3所示。工控机通过以太网总线向运动控制卡发送控制指令,运动控制卡根据指令值控制电机运转,实时采集电机编码器反馈的脉冲值,根据反馈值计算电机实际转动的角速度;将电机的实际角速度实时反馈给工控机,工控机将对应时刻的角速度值写入相关文档,用于相关参数辨识。
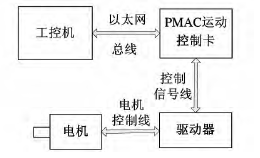
图3 实验平台结构


3.2 参数辨识
实验输入的指令是一系列阶跃电压信号,指令电压先增大再减小,共进行3组实验,如图4所示。3组实验中,指令电压值从0增加到每组实验的最大值,再减小到0,相应阶跃点的控制电压值如表1所示,3组实验的最大值分别为75mV、100mV 和150mV,最小值为0。
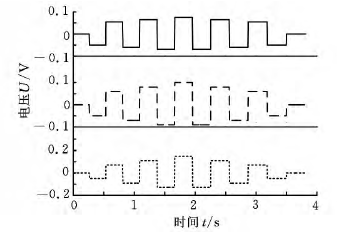
图4 3组实验指令电压信号
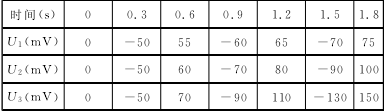
表1 指令电压值
利用 PMAC 运动控制卡实时采集电机的速度值,利用式(7)和式(14)分别对系统的参数进行估算,得到转动惯量、黏性摩擦和库仑摩擦转矩的估计值。表2是通过简单二乘法获得的转动惯量和黏性摩擦值。表3是通过无偏差最小二乘法得到的转动惯量、黏性摩擦值和库仑摩擦转矩值。图5是3组实验的估算值对比图。
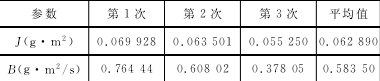
表2 简单最小二乘法估算值
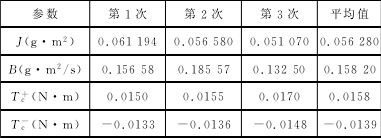
表3 无偏差最小二乘法估算值
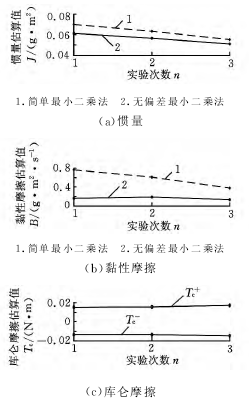
图5 实验数据对比
对比3组实验的估算值,简单最小二乘法得到的转动惯量和黏性摩擦值相对较大,且3组实验结果存在较大差异,无偏差最小二乘法3组实验得到的估算值波动较小,三次实验的结果基本一致。由表2可得简单最小二乘法3组实验的平均估算值为

对比实际和辨识所得的伺服控制平台的转动惯量值,从以上的估算结果可以看出,两种方式估算得到的转动惯量值都很接近实际值,两种方式都能很好地辨识系统的转动惯量。然而,简单最小二乘方式辨识得到的转动惯量和黏性摩擦的值相对无偏差方式较大,而且3次辨识的结果差别较大。简单最小二乘法未考虑库仑摩擦的影响,将库仑摩擦的影响转化成黏性摩擦的影响,致使黏性摩擦和转动惯量 值增大并使得结果波动较大。
为了验证辨识参数的有效性和准确性,将辨识获得的参数代入到理论模型中,根据输入的电压指令计算并重构理论角速度,将理论角速度与实测角速度相比较,结果如图6所示。
采用简单最小二乘方式重构的角速度最大误差值为15rad/s,无偏差方式重构的角速度误差值为7rad/s,不到前一种方式 的一 半,采 用 无 偏 差 方式辨识获得的参数重新构建的角速度与实际的角速度相符度更高,更能准确地描述实际伺服系统。
采用无偏差方式估算的参数计算得到的理论角速度曲线更接近实测角速度曲线,而且角速度误差波动更小。
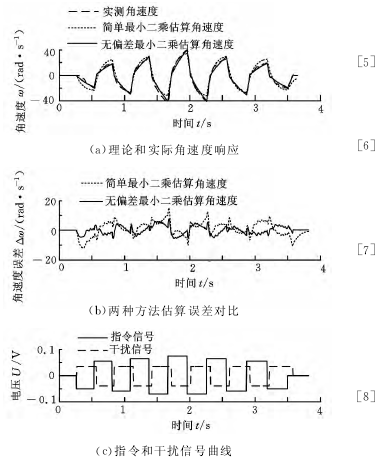
图6 角速度重构与分析图
4、结语
本文分析了伺服控制系统结构模型,采用无偏差最小二乘方法,基于“库仑摩擦+黏性摩擦”模型,辨识伺服控制系统参数。研究了最小二乘法参数辨识在“工控机+运动控制卡”数控平台上的实现方法,从理论和实验的角度分析了辨识方法的准确性。通过辨识实验获得系统的参数,并将估算得到的系统参数代入系统模型,重构电机角速度。实验结果表明,所采用无偏差最小二乘方法可以更准确地辨识系统的参数。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息




