某加工中心滑座的动态特性测试与优化
2020-2-25 来源:沈阳理工大学机械工程学院 沈阳机床 作者:史安娜 刘斯妤 曹富荣 马晓波
摘 要: 针对立式加工中心滑座的动态特性直接影响整机的加工精度等问题,以某型号加工中心为研究对象,采用有限元分析和试验分析相结合的方法,进行静动态特性分析。利用 SolidWork 软件进行三维模型的建立,使用 Ansys Workbench 软件对该加工中心进行动态特性分析,对关键尺寸进行灵敏度分析,选择对滑座性能影响较大的尺寸进行优化设计。采用遗传算法对不同的优化目标进行优化,最终得到优化后的加工中心滑座的前四阶固有频率和总质量有了明显改善,提高了机床加工的精确度。
关键词: 加工中心; 动态性能; 优化设计; 灵敏度分析
滑座作为加工中心的基础部件,既是工作台的支承件,也是伺服进给系统的运动部件,其质量和受力变形直接影响工作台的回转进给和直线进给精度,因此,如何控制好滑座的结构振动特性是设计人员面临的主要技术难题之一。
当今,国内的科研工作者对机床的结构设计从传统的经验类比法逐步转向有限元法等分析软件计算法。郑文标等通过有限元分析和灵敏度分析,找到了床身结构的薄弱尺寸,再通过对比优化前后的固有频率,验证了优化的有效性。孙晓俊等人应用 ANSYS 优化了某齿轮复合加工机床立柱的尺寸,寻找出最优解。范晋伟等人利用 Ansys Workbench对垫板进行模态分析,根据振型图找出其薄弱部件,再对比 5 种优化途径,提高了垫板的固有频率。
这些科研工作者的优化设计都取得了很好的优化结果。但上述研究均以部件的单个性能作为优化目标,并没有对机构的综合性能进行优化。本文以某立式加工中心为研究对象,在对滑座进行理论、试验模态分析的基础上,分析其动态特性。运用灵敏度分析在滑座的众多尺寸中找出对质量、一阶固有频率影响最大的 3 个参数。建立神经网络模型,分析出这些参数与滑座一阶固有频率和质量的非线性关系,最后通过多目标遗传算法寻求最优解。在满足强度的情况下,减轻了滑座的质量,并提高了其动静态性能,为滑座的设计提供了参考。
1、 有限元模型的建立
为了保证分析的准确性,根据滑座的图纸 1: 1 建立三维模型,并且设置材料性能。该滑座材料为 HT300,杨氏模量为 1. 43×1011Pa,泊松比为 0. 27,材料密度为7. 3×103kg / m3,滑座有限元模型,如图 1 所示。
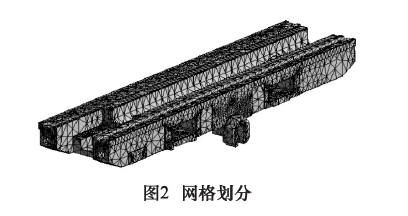
网格划分的结果对有限元仿真速度和精度有较大影响,通常来说,划分的网格数目越多,计算精度越高,但计算速度较慢,因此划分网格时要选择适当精度的网格。本文通过自动划分网格法划分网格,在设置相关参数后,得出节点数为 164 447,单元数为168 235,划分的模型如图 2 所示。
2 、滑座动力学分析
2. 1 理论模态分析
目前机床结构的理论模态分析,通常利用计算机软件进行有限元分析。主流的有限元分析软件主要有Ansys、Abaqus、Admas 等等。本次研究中,采用 AnsysWorkbench 17. 0 软件进行模态分析,可以和 Solidwork三维制图软件进行数据对接,方便改变滑座的尺寸参数。首先设定滑座的边界条件,使边界条件和试验模态分析的一致,提取滑座的各阶固有频率。前四阶固有频率,如表 1 所示,振型如图 3 所示。
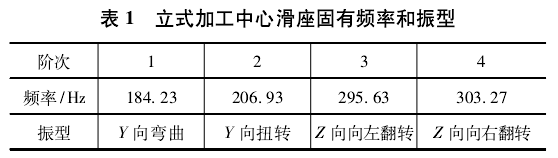
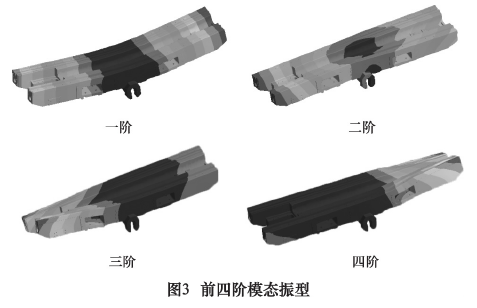
2. 2 试验模态分析
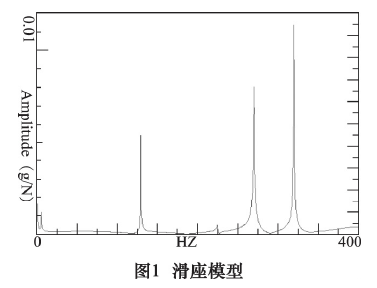
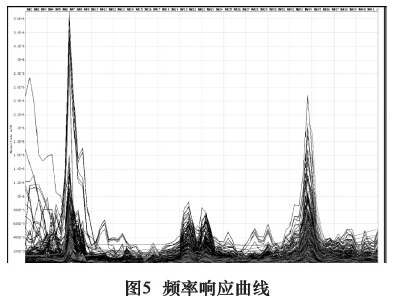
本实验采用 B&K 公司的 7700 Pulse 多通道动态信号采集分析系统、4507B 型内置放大电路型加速度传感器、YC2 模态试验力锤等设备来记录分析数据,如图 4 所示。将滑座放置在隔振台上,布置了 70 个测点,通过单点激励、多点识振的方法,获取模态振型,图5 为频率响应曲线。

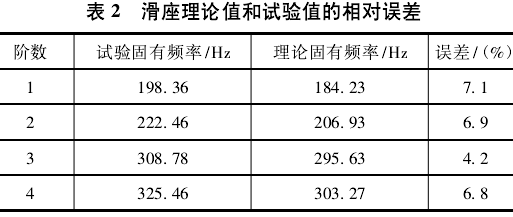
对该型立式加工中心进行模态实验分析,获得前四阶固有频率与振型,理论模态分析和试验模态分析结果的对比如表 2,可以看出,两者的误差在 10%之内,说明该有限元模型是有效的,边界条件的设定与工作状况一致。
3 、滑座优化
3. 1 对滑座参数的灵敏度分析
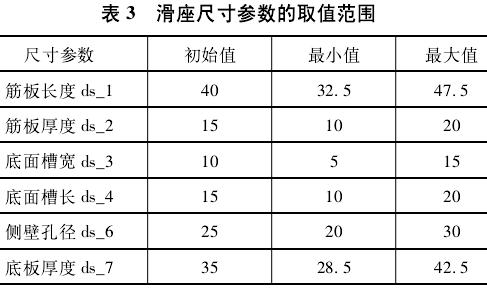
此加工中心的滑座有很多尺寸参数,为了减少计算量,需先对滑座尺寸进行灵敏度分析,找出对一阶固有频率和总质量影响最大的尺寸,将其作为尺寸参数。对滑座结构进行分析后,选取 5 个尺寸进行分析,如表3 所示。分析后得到灵敏度分析图,如图 6 所示。
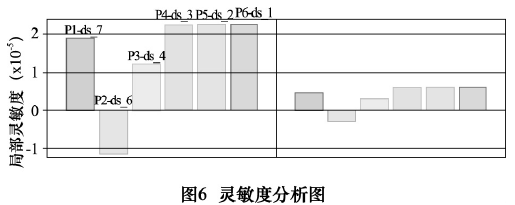
从图 6 可以看出,对滑座一阶固有频率和总质量影响比较大的尺寸依次为筋板长度 ds_1 、筋板厚度ds_2 、底面槽宽 ds_3 。
3. 2 神经网络建模
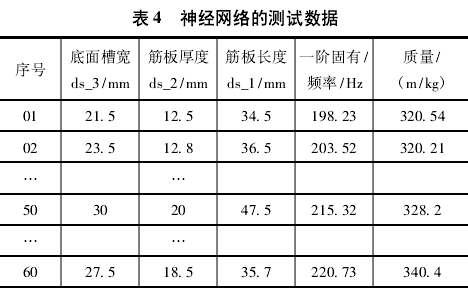
BP 神经网络拥有很好的非线性映射能力,并且结构简单,计算速度快,可以较为便捷的解决多目标优化问题。因此对于滑座的 3 个尺寸参数可以建立输入输出映射,建立其与一阶固有频率和总质量的关系,进行样本点的学习。由于滑座的模态分析试验耗时很长,无法为神经网络算法提供快速、大量的样本数据,因此只考虑实验点在实验范围内均匀散布的数据,即采用均匀设计法进行样本点的输入,大大提高了数据的有效利用性,并且减小了神经网络的误差。表 4 为神经网络的测试数据,前 50 组为训练数据,即对权值和阈值进行修正,直到收敛为止,第 50 ~60 组为测试数据。
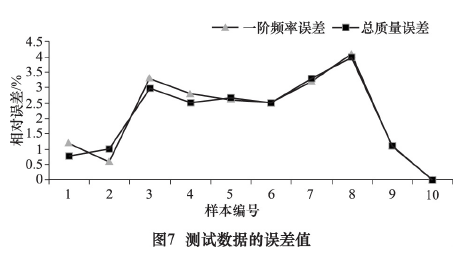
为了防止神经网络误差过大,用第 50 ~ 60 组测数据对神经网络模型进行测试,如图 7 所示,误差均在5%之内。由此可知,该测试数据有效,可以进行下一步的分析。
3. 3 遗传算法寻优
由于当今机床的发展朝着绿色、轻量化的方向发展,因此关于此滑座的优化可以采用一阶固有频率的最大并且总质量最小为目标进行多目标优化。而且对一阶固有频率进行优化是为了避免一阶固有频率和激励频率相近,而引起共振现象的产生,因此使得一阶固有频率大于等于激振频率 210 Hz。多目标优化问题描述为:

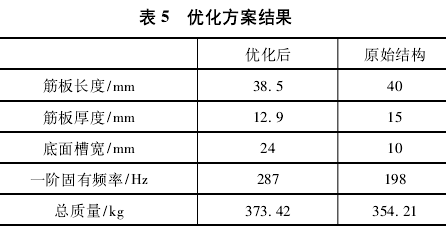
优化方法采用遗传算法,是计算机科学人工智能领域中用于解决最优化的一种搜索启发式算法,是进化算法的一种。通过测试验样本数据建立优化目标方程,使用 Matlab 的 GA 工具箱,对该优化目标求解,得出的一阶固有频率和总质量带回到 Ansys Work-bench 中分析结果,如表 5 所示。表中,优化后的方案为多目标优化的结果,通过比较得出优化后的一阶固有频率有明显的提高,并且远离激振频率,避免共振。滑座的总质量下降了 19 kg,实现了滑座的轻量化设计,达到了优化目的。
4 、结语
本文针对某型号加工中心进行优化设计,先进行理论与试验模态分析,分析后的结果误差较小,说明有限元模型建立有效。以此为基础,进行灵敏度分析,找出影响较大的尺寸参数,采用均匀设计法进行神经网络的训练。最后采用了多目标优化的方法,得到了合适的优化方案。为后续机床零部件的设计提供了参考方案。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息





