基于半闭环进给系统的水刀机床建模与仿真研究
2015-8-28 来源:数控机床市场网 作者:杨志君 马诠和 赵不贿 陈波
杨志君1,马诠和2,赵不贿1,陈波2
(1. 江苏大学电气信息工程学院,江苏镇江 212013;
2. 南京大地水刀股份有限公司,江苏南京 211300)
摘要: 以某公司生产的半闭环控制的悬臂式水切割机床 DWJ2030_FB 为分析对象,建立其简化数学模型,对影响机床运行性能的转动惯量比、反向间隙及传动机构刚性进行了仿真分析,同时利用安川 SigmaWin + 软件和 Renishaw 激光干涉仪对分析结果进行了测试验证。仿真及试验结果表明: 降低进给轴的转动惯量比有利于提高系统动态响应及稳定性,转动惯量比接近或小于 1 时为最佳; 滚珠丝杠反向间隙是机床定位精度降低、产生轮廓误差的因素之一,采用激光干涉仪补偿可有效降低反向间隙的影响; 传动机构刚性的增大有利于系统响应性、定位精度和稳定性的提升,而刚度达到一定值时,则不能再通过刚度的提高来提升系统性能。
关键词: 超高压水射流; 机床控制; 转动惯量比; 反向间隙; 刚性
0 前言
进给驱动系统是数控机床最为重要的组成部分,它的性能指标在一定程度上直接决定了机床的静态、动态特性,在高速、高精度、多轴联动等场合显得尤为突出。与普通数控机床相比,水切割速度快、柔性好、悬臂及龙门结构能满足各类切割尺寸,但其切割精度并不高。对于半闭环结构的水刀机床,其进给系统在机械传动部分无检测元件和反馈环节,当负载特性、外界干扰、摩擦等非线性因素作用于滚珠丝杠、导轨等机械传动机构时,将直接影响到机床的动态响应性、稳定性、尺寸及轮廓精度等。因此分析各类非线性因素的影响,将有助于提高半闭环结构水刀机床的整体性能。
1 水刀机床进给系统建模
1. 1 半闭环控制的进给系统原理
图 1 为大地水刀悬臂式机床产品 DWJ2030_ FB,主要由 ESA 数控系统,安川∑- Ⅴ系列交流伺服驱动器及伺服电机构成的半闭环控制结构,其进给系统原理框图如图 2 所示。CNC 一方面进行插补处理、发送控制信号,另一方面接收驱动器从电机编码器反馈回来的位置信号,进行比较补偿处理; 伺服单元将CNC 发送的电信号转换成电机轴上的角速度输出,同时接收来自电机编码器的速度和位置反馈; 机械传动机构则通过滚珠丝杠、皮带等装置将电机的旋转运动转换成直线位移输出。

1. 2 数控系统的数学模型
机床的控制方式主要分为: 位置控制、速度控制和扭矩控制。半闭环系统常用速度控制方式,由CNC 发送 -10 ~ + 10 V 的模拟量电压来控制各轴移位; 给出了速度控制时 CNC 与伺服单元的连接控制图,在不考虑转矩前馈等因素时可将CNC 简化为一个位置控制单元,传递函数可用一个比例系数 KP来代替,结构框图如图 3 所示。
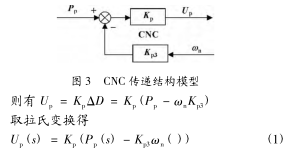
1. 3 速度控制时伺服单元的数学模型
伺服单元包括伺服驱动器和伺服电机,其自身由电流环、速度环和位置环构成一个全闭环控制系统。速度控制时处于最外层的位置环不起作用,由 CNC代替,CNC 将插补指令转变成模拟电压指令后直接传送至速度环。速度环的作用是增强系统抗负载扰动的能力,抑制速度波动,它由速度前向滤波器、速度调节器、速度反馈构成。电流环处于最内层,它是提高伺服控制系统精度和响应速度、改善控制性能的关键,由电流前向滤波器、电流调节器、矢量控制算法和电流反馈构成。
给出了速度控制时伺服系统的典型五阶模型,包括速度环、电流环以及交流伺服电机的数学模型,利用极点配置的方法给出了伺服系统在高速运行特性下的四阶模型。由于实际伺服单元各环节具有非线性、时变、机电耦合等关系,因此在工程实际研究中,可忽略各环节的反馈、滤波等影响,将速度环、电流环分别简化成 PI和 PID 控制器,结构框图如图 4 所示。
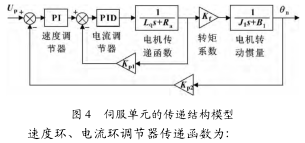

1. 4 机械传动结构的数学模型
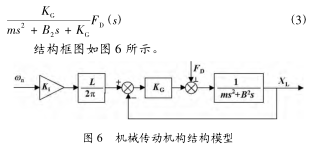
在 DWJ2030_FB 悬臂机床上,传动方式包括直连(x 轴) 和皮带传动 (y 轴) 两类形式,图 5 所示为皮带传动结构方式,以下建模以该类型传动方式为例。
图 5 皮带传动方式结构
机械传动和执行单元的输入为电机的角位移 ωn,输出为移动工作台的直线运动 XL,其机械系统动力学平衡方程为:

1. 5 DWJ2030_FB 悬臂机床单轴进给系统仿真模型
由于水切割为非接触式的冷态切割方式,即刀头与工件不接触,在忽略水对刀头的反作用力之后,可等效认为加工时工件对工作台的反作用力 FD为 0。同时,为便于仿真比较转动惯量的影响,将工作台的重量等效成为折算到滚珠丝杠上的负载惯量 J2。综合公式 (1) (2) (3),便可得到如图 7 所示的机床单轴进给系统仿真模型,表1 为其主要参数列表及取值。
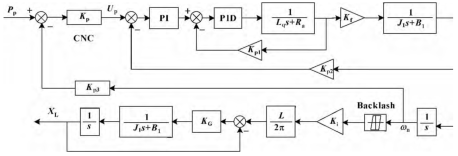

2 仿真分析
半闭环结构的机床进给系统在机械传动部分无检测元件和反馈环节,受负载特性、外界干扰等非线性因素影响较大,从而直接影响到机床性能,因此必须考虑作用于机械传动机构上的各因素影响。
2. 1 转动惯量比
通过传动机构折算到滚珠丝杠上的负载惯量 JL与电机轴转子惯量 Jm的比值即为转动惯量比。同传动方式下,负载越重,折算到滚珠丝杠上的负载惯量 JL也越大。由于 Jm为一定值,即可通过模拟改变JL来分析二者的关系,仿真时负载惯量 JL分别取0. 5、1、2、3、5 倍的转子惯量 Jm,所得仿真波形如图 8 所示。
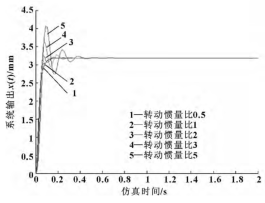
由仿真波形可得: 转动惯量比越大,系统越不稳定,超调量 σ、上升时间 tr和调整时间 ts均逐渐增大,使系统启动响应延迟、调整时间长; 转动惯量比越小,系统的动态响应特性越好且越容易稳定,当转动惯量比小于一定值时,系统的阶跃响应特性基本不变; 因此对于高响应要求的机床,在设计时应尽量减轻横梁等工作台的负重,以减小折算到丝杠上的负载惯量,JL/Jm接近或小于 1 为最佳; 同时要考虑与电机转子惯量的匹配,从而提高机床的动态响应性和跟随性。
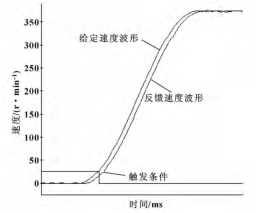
(0. 95) 后利用安川 SigmaWin + 软件实测放大的机床y 轴启动特性转速曲线,其上升转速平滑,反馈转速跟随性较好,无超调,动态响应较快。试验还发现:当未能正确估测机床各轴转动惯量比或对于负载惯量较大的进给轴,其快速运行时会产生一定的轴振动。通常对于电机转子与滚珠丝杠由联轴器直接相连的传动方式,其负载惯量将全部折算至丝杠上,导致转动惯量比增大。而利用减速机和皮带传动的组合,折算至滚珠丝杠上的负载惯量将按减速比的平方次削减。因此,在大负载的机床上,为降低负载重量对机床性能的影响,可广泛应用带减速机与皮带的传动方式。
2. 2 反向间隙
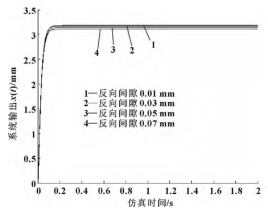
对于完全没有间隙的结构,机床的磨损将是非常严重的,因此传动过程中往往会留有较小的间隙,为分析间隙对进给系统的影响,特别是对最主要的滚珠丝杠反向间隙进行研究分析,仿真时在模型中引入间隙模块 Backlash,反向间隙值分别取 0. 01,0. 03,0. 05,0. 07 mm,所得波形如图 10 所示。
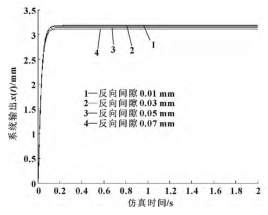
显然,当反向间隙从 0. 01 mm 至 0. 07 mm 变化时工作台移位曲线滞后也越来越明显,与实际定位点的偏差加大,工作台输出位移的位置误差增加,定位精度降低。若机床进行轮廓加工时,过大的反向间隙更会影响切割质量。
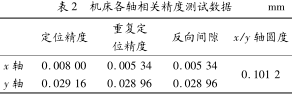
表 2 为利用雷尼绍激光干涉仪实测的 DWJ2030_FB 机床 x、y 轴相关精度,各轴通过激光间隙补偿、螺距补偿,有效地消除了滚珠丝杠反向间隙的影响,重复定位精度较未补偿前的定位精度得到了提高,精度标准均满足公司设备出厂检验标准,因此相比利用全闭环结构提高传动精度,半闭环系统采用激光干涉仪补偿是消除间隙、提高精度最为有效简便的方法。
2.3 传动机构刚性
刚性为机械刚度的指标,滚珠丝杠的刚性取决于丝杠与螺母间轴向负荷珠槽接触刚性及丝杠轴的刚性。为分析传动机构刚性对进给系统的影响,仿真时将各类刚性简化成为一个传动机构总刚性 KG,分别取值为 50、100、200、300、400 kgf/μm,所得波形如图 11 所示。
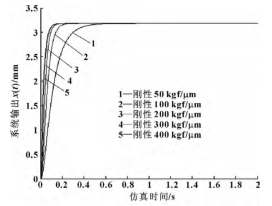
显然,传动机构刚性的增大可提高系统的响应特性,缩短稳定时间,减少系统的随动误差,从而提高系统的定位精度,同时机床抗干扰的能力也越强,稳定性越高,当刚度达到 300 ~400 kgf/μm 时,系统的阶跃响应特性基本保持不变,可见当机构刚度达到一定值时,不能再通过刚度的提高来提升系统性能。表2 中 x 轴为直连形式,与 y 轴皮带传动相比刚度较大,因此无论其定位精度还是重复定位精度均优于 y 轴,同时通过激光干涉仪补偿后,重复定位精度较未补偿前的定位精度得到明显提升,可见刚性较小时产生的较大弹性形变容易造成定位偏差。因此,直连传动和通过减速机与皮带传动两类形式各有优劣,设计安装时应综合考虑、折中选取、尽量提高各环节的刚性。
3 结束语
以南京大地水刀有限公司生产的半闭环悬臂式水切割机床 DWJ2030_FB 为例,构建了该机床的半闭环控制简化数学模型,并利用 Matlab/Simulink 仿真模块对机床转动惯量比、反向间隙、传动机构刚性进行了仿真与验证,分析了这些因素作用于半闭环进给系统不可控部分时的影响以及解决方法,对提高半闭环控制系统的性能、机械传动部分的选型和设计,提供了较强的理论参考依据。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息





