错齿内排屑刀具深孑L/Jn工中的刀具振动特性对孔圆度形貌的作用机制
2016-11-23 来源:西安理工大学机械与精密仪器工程学院 作者:孔令飞,牛晗,侯晓丽,林宏斌,王杰
摘要:依据错齿内排屑刀具深孔加工的实际特点,构建了受刀具横向振动特性影响的加工孔圆度形貌模型。运用动力学半解析法,在保证刀具系统动态分析精度的前提下,将复杂深孔刀具系统离散为多段具有局部特征的梁单元,其中相邻单元之间满足模态形函数传递矩阵的连续条件。结合Newton—Raphson迭代法,给出了深孔圆度形貌形成轨迹的数学描述,以及深孔刀具动态特性与加工孔圆度形貌之间的关联关系。通过数值算例验证了所提出方法的可行性,同时为实现深孔切削过程加工孔圆度误差的预测与控制奠定了基础。
关键词:机械制造工艺与设备;深孔钻削;刀具振动;圆度形貌;半解析法
0.引言
精密高效的错齿内排屑刀具(BTA)深孔钻削技术是当今兵器工业、新能源装备制造和高新技术产业对深孔零件加工提出的迫切需要¨。4 o。然而,由于深孔钻削机理的复杂性,实际加工中刀具系统需要承受切削力波动及刀具回转惯性等的影响,而这些载荷又随着加工参数的变化而变化,致使刀具所表现出的动态行为极其复杂,进而对加工孔品质产生极大影响¨。。那么,如何构建更加精确的深孔刀具系统动态模型,探明加工参数与加工孔精度的映射关系,实现高效、准确地预测与控制加工孔品质,就成为深孔钻削研究的热点和关键问题。
Mehrabadi等M1构建了考虑钻削过程阻尼和质量偏心影响的刀具系统动力学模型,讨论了刀具动态运行轨迹及其相应的孔圆度形貌特征,并结合实验证实了该模型的准确性。Bayly等依据钻削加工过程的实际特点,研究了颤振对钻削刀刃切削力和碰摩力的影响,分析了叶瓣孑L的成形机理。在此基础上,Deng等"o运用Euler.Ber.noulli梁单元模型,并结合深孔切削力的傅里叶函数形式表达式,给出了深孔加工圆度误差计算模型,进而对波纹型与叶瓣型深孔的形成机理进行了研究。但是,由于刀具系统结构的复杂性,这些将切削力简化为一阶径向波动分量形式".10],或是将刀杆简化为简支梁模型,以期得到加工孔圆度形貌的数值解或解析解,就不可避免地丢失刀具系统的一些动力学特性。在实际的深孔加工刀具系统中,刀具经常是由多个部件组成的连续体,且包含有多段刀杆及特殊构造的刀头,因而难以用简单模型来描述,必须构建更加精确的深孔加工刀具系统模型。
针对上述问题,本文将复杂深孔刀具系统离散为多段具有局部结构特征的梁单元,而相邻单元之间满足模态形函数传递矩阵的连续条件。然后,利用Newton—Raphson迭代法,并结合BTA深孔钻削力的傅里叶多阶谐波形式,给出了深孔圆度形貌形成轨迹的解析形式。据此,研究了深孔刀具动态特性与加工孔圆度形貌之间的关联关系,以及在深孑L低速切削过程中易出现叶瓣孑L型的成因及其机理。数值算例验证了本文所提出方法的可行性,该方法将为实现深孔切削过程加工孔误差的预测与控制奠定基础。
1.BTA深孔钻削系统的动态方程
1.1 BTA深孔钻削系统的模型
深孔钻削加工是将特殊构型的切削刀具装在圆形空心钻杆上,使得工件相对于刀具作高速旋转运动(或刀具相对于工件作高速旋转运动)。通过授油装置将高压切削液沿着钻杆与孔壁之间的缝隙喷人切削区域,利用切削液自身压力实现刀具切削部分排屑、冷却和润滑。图1为钻杆系统示意图,其中喈邢为旋转坐标系,OXYZ为固定坐标系,二者转换关系为f=Xcos(亿)+Ysin(亿)、r/=一Xsin(亿)+Ycos(亿)和z=Z乒以是钻杆承受的切削力分量,力为钻杆旋转角速度。
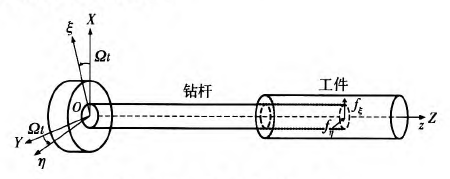
图1 深孔钻削刀具系统示意图
采用Lagrangian变分原理,如图1所示的深孔刀具系统应满足:
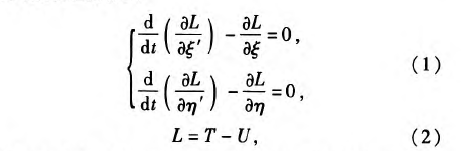
式中:L为拉格朗日函数;T为刀具系统动能;U为刀具系统势能;“”’表示1阶导数。依据Euler.Ber—noulli梁理论,取旋转钻杆模型在受弯状态下的一个微分单元如图2所示,图中P为径向力,Q为剪力,M为弯矩,p为密度,S为横截面面积。
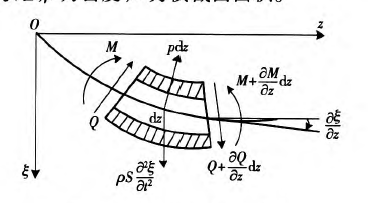
图2 BTA钻杆微分单元
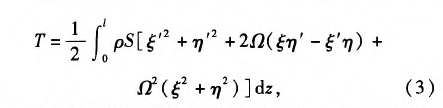
式中:出为钻杆长度方向的微分单元;z表示钻杆长度。同理,深孔刀具系统钻杆的势能表达式为

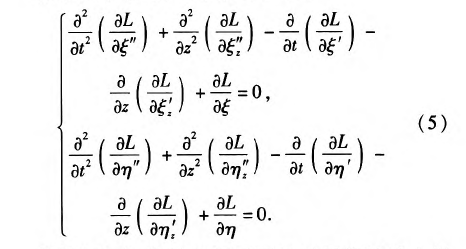
依据(5)式,旋转坐标系下刀具系统的动力学方程可表示为

1.2 BTA深孔加工刀具的动态切削力


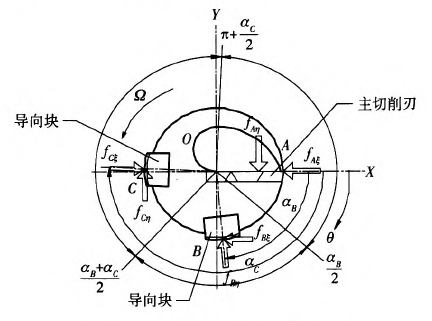
图3 BTA深孔加工切削力分布

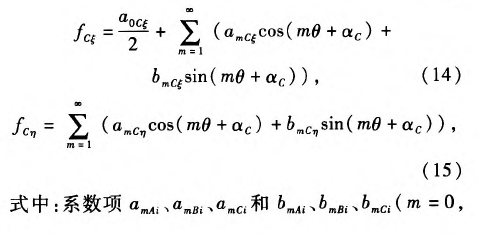

2.深孔圆度形貌的形成轨迹
为了便于获得被加工孔圆度形貌的轨迹特征,可将广义坐标系下旋转钻杆的振动方程转化到复平

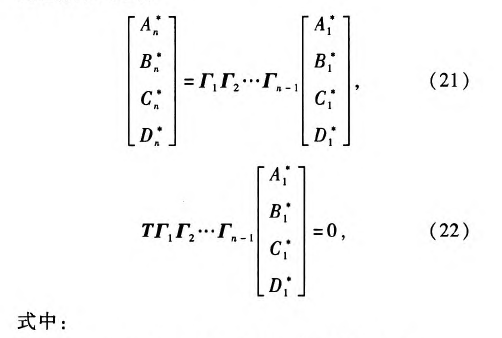
若要精准地预测孔圆度形貌轨迹,就必须考虑刀具系统中具有局部结构特征的部件(例如:刀杆连接螺纹、刀头等)对系统动态方程(17)式所产生的影响。因此,依据图4所示的划分规则,将深孔刀具系统离散为多段具有均匀结构特征的梁单元,图4中Zi为相应结构单元的长度,i=1,2,......,n.
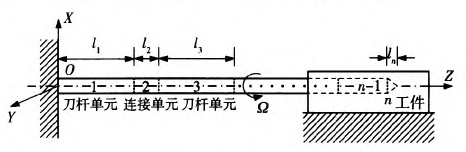
图4深孔钻削刀具系统模型
图4中,经离散化处理后的深孔刀具系统可分为凡个结构单元,其中第i段梁的模态函数为






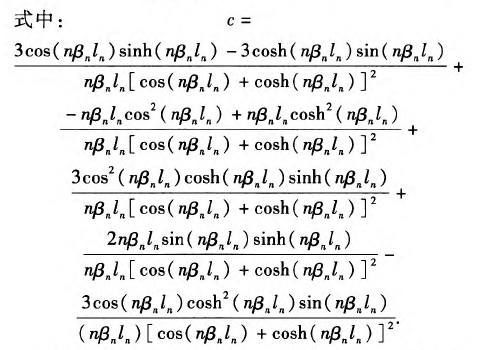
由此可见,(26)式是关于时间函数q(t)的2阶线性微分方程,故采用Laplace变换的方法求解,并将其转化到原物理空间,方程(17)式解的具体形式可写为
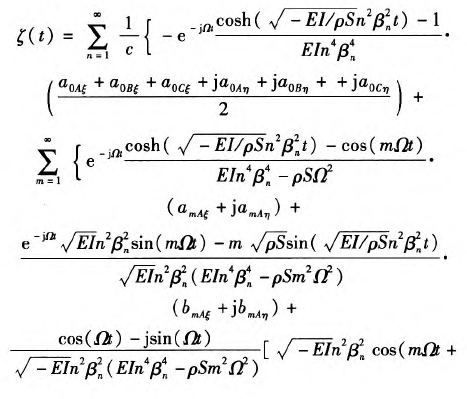
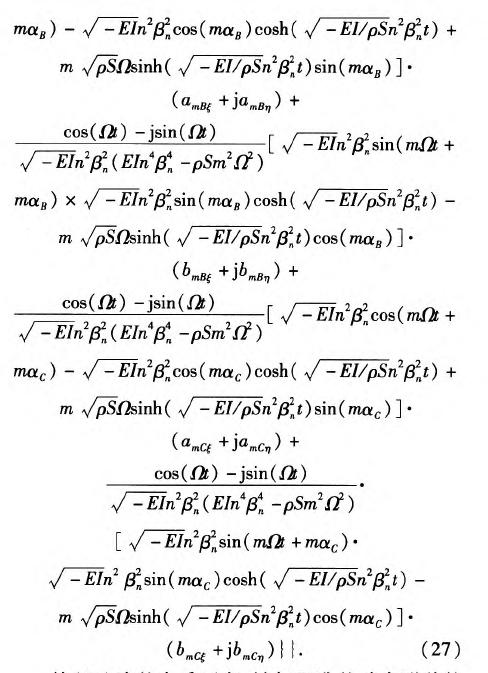

3.方法验证
为了验证方法的可行性,运用上述理论和算法编制程序,将计算结果与文献[7]的实验结果进行对比。相关计算参数如下:钻杆材料密度为7 860 kg/m3,弹性模量为2.06×10¨Pa;刀具直径分别选用18.91 mm和26.40 mm两种,其中刀具直径为18.91 mm时,钻杆的内径与外径分别为11.5 mm和17 mm,而当刀具直径为26.40 mm时,钻杆的内径与外径分别为14 mm和22 mm.
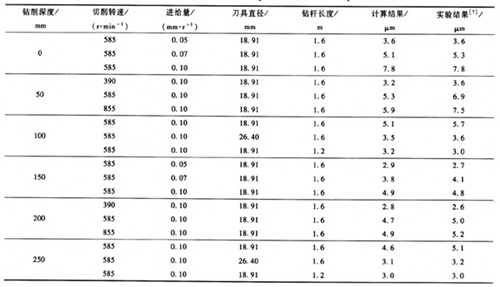
表1为在不同切削转速、进给量及加工深度条件下,计算得到的被加工孔圆度误差数值。由表1可以看出,当选定加工深度时,若改变钻削进给量、切削转速或钻杆直径参数,被加工孔圆度误差的预测结果与实验结果的变化趋势是相同的,即随着钻削进给量的增加、切削转速的增大及钻杆直径的减少,被加工孔的圆度误差均在不同程度上增大。例如当选定加工深度为150 mm时,钻削进给量从0.05 mm/r增加到0.1 mm/r,圆度误差的预测结果从2.9肛m增加到4.9斗m,而实验结果则从2.7“m增加到4.8斗m;若选定加工深度为200 mm时,切削转速从390 r/min增加到855 r/min,圆度误差的预测结果与实验结果分别从2.8斗m增加到4.9¨m和从2.6斗m增加到5.2斗m.此外,尽管孔圆度误差的预测结果与实验结果存在一些差异,但二者之间的误差几乎都在10%以内,这表明本文所提出的方法适用于预测被加工孔的圆度误差及其变化趋势,且具有较高的精度。然而,就预测结果与实验结果之间的差异而言,主要是由于本文采用的切削力模型尚存在不足之处,例如导向块与孔壁表面之间的摩擦效应、材料本身的性能等因素未被考虑。
表1 圆度误差的理论计算与实验结果对比
4.应用算例与分析
本节将运用前文所述的算法编制程序,探究不同切削转速条件下,刀具中心动态轨迹与孔表面圆度形貌之间的关联联系,进而为实际加工过程中精准预测或控制被加工孔的圆度误差奠定基础。图5~图7分别给出了当进给量为0.I mm/r、钻杆长度为I.6 m及刀具直径为18.91 mm时,选取390 r/min、560 r/min和830 r/min 3种不同切削转速进行加工,获得的刀具中心动态轨迹。从图5一图7中可以看出,随着切削转速的增大,刀具中心动态轨迹的振动范围不断增大,但振动特征却呈现出明显差异。例如当刀具转速为390 r/min时,刀具中心的动态轨迹呈现出明显的4波瓣轨迹,而切削转速为560 r/min和830 r/min时,上述现象却并不明显。
为了进一步研究孔圆度形貌的形成机制,可取上述相同的加工参数,绘制出孑L圆度形貌轨迹,如图8所示。从图8中可以看出,对于3种不同的切削转速而言,刀具每切削一个周期所形成的圆度形貌轨迹与相邻两周之间均存在着一个相位差占,,进而造成了相邻切削周期内所形成的孔型存在角度差异。若相位差占。越小,则相邻切削周期的孔型偏差也就越小。结合Bayly等¨1和Tlusty¨钊的研究可知,孔圆度形貌的偏差与刀具系统固有特性有着直接联系。
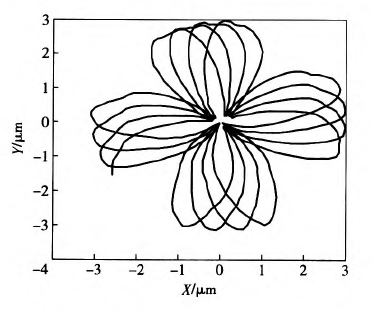
图5 当力=390 r/rain时刀具中心的动态轨迹
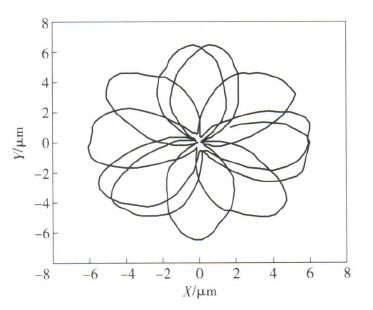
图6 当n=560 r/min时刀具中心的动态轨迹
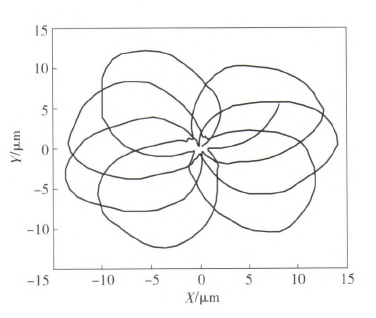
图7 当n=830 r/min时刀具中心的动态轨迹
基于此,利用本文所述的数值计算方法,获得深孔刀具系统的第1阶固有频率为25.2 Hz,将其转化成相应的转速单位为1 5lO.8 r/min.若选取切削转速为390 r/min时,该值恰好接近于固有频率的四分之一(即377.7 r/min),因而被加工孔圆度形貌呈现出明显的4瓣特征,如图8(a)所示。图9一图12给出了当切削转速分别为深孔钻杆系统第1阶固有频率的1/2、1/3、1/4和1/5时,计算获得的刀具中心动态轨迹,相应的波瓣数为2瓣、3瓣、4瓣、5瓣。通过上述数值算例可以看出,虽然实际钻削中引发孔圆度形貌变化的原因不同,但其形成的过程和出现的规律是相同的,即孔圆度形貌与刀具系统的低阶固有频率及激励频率有着最为直接的联系。
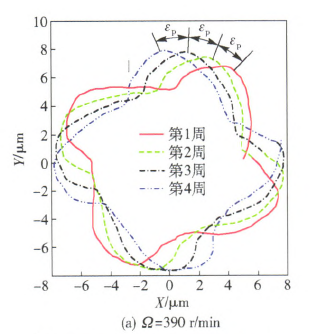
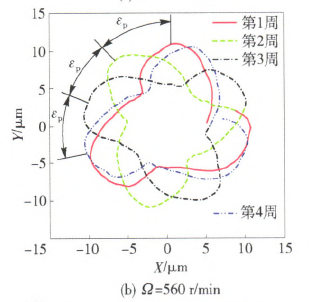
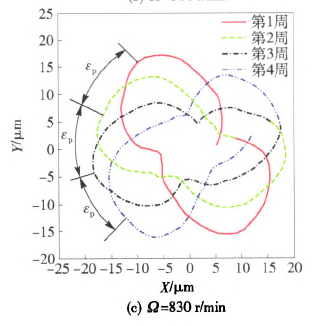
图8 不同转速时孔表面圆度的二维形貌轨迹
5.结论
考虑到实际深孔加工刀具系统结构的复杂性,将刀具系统离散为多段具有局部结构特征的梁单元,其中相邻单元之间满足模态形函数传递矩阵的连续条件,进而构建了深孔圆度形貌形成轨迹的解析表达式。运用该数值计算方法,研究了刀具动态特性与加工孔圆度形貌之间的关联关系。由数值计算结果可以看出,虽然深孔钻削过程中引发孔圆度误差变化的原因不同,但其形成的过程和出现的规
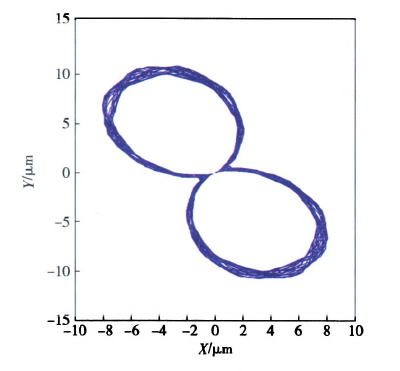
图9当n=755.4 r/min时刀具中心的动态轨迹
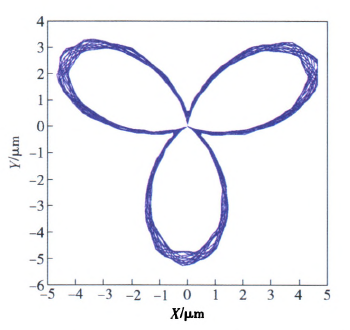
图10 当n=503.6 r/min时刀具中心的动态轨迹
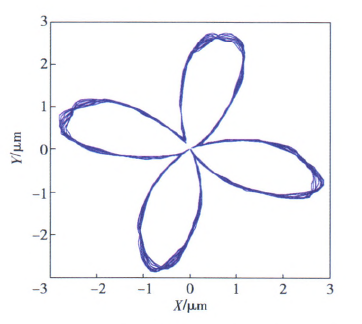
图1l 当力=377.7 r/min时刀具中心的动态轨迹
律是相同的,即孔圆度误差形貌与刀具系统的固有频率及激励频率有着最为直接的联系。此外,算例结果也验证了本文所提出的方法适用于探究被加工深孔圆度误差的变化规律,这些将为实现深孔切削过程加工孔圆度误差的预测与控制奠定基础,且具有足够的精度。
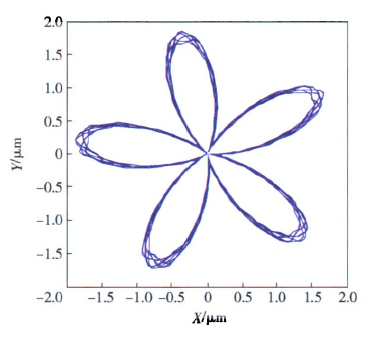
图12 当1-1=302.16 r/min时刀具中心的动态轨迹
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息





