BTA 深孔加工系统中工件的振动分析
2019-3-7 来源:中北大学; 山西省深孔加工工程技术研究中 作者:吴竹兵 沈兴全 范春义 胡宽辉
摘要: 将深孔加工中的工件简化成两端固定支撑的旋转梁,建立工件的动力学模型,运用梁理论得到工件的自由振动方程,利用 MATLAB 拟合分析在不同切削位置、不同主轴转速和不同进给量情况下工件的振动偏移量。分析结果表明,加工到工件的不同位置时,工件的偏移量不同,中心处工件偏移量最大; 增大刀具的进给量,工件的振动偏移量增大; 转速的变化对工件的振动影响较小。
关键词: 深孔加工; 工件振动; 梁理论; MATLAB 拟合
1、 引言
深孔加工中的振动会导致切削不稳定并影响加工表面质量,造成加工零件精度低、刀具严重磨损、加工效率降低等问题,因此,切削加工中发生的振动成为影响深孔加工质量的关键因素和重要研究内容。
目前的研究主要集中在振动产生的原因及消除方法、再生型颤振、刀具系统的动态稳定性和钻杆扭转振动减振技术等方面。在深孔加工过程中,钻头的旋转会引发陀螺效应,对颤振产生影响。Mehrabadi 等考虑到这方面的因素,通过深入分析得到了更加完善的颤振模型。Tobias 考虑到工艺阻尼和刚度对振动的影响,将机床的动态特性和加工过程结合起来,构建了更完善的自激振动和颤振模型。
本文以工件旋转、刀具进给的加工方式,把工件简化成两端固定的旋转梁,运用 Rayleigh 梁理论结合 MATLAB 软件分析了工件在不同加工阶段的振动情况以及主轴转速和进给量对工件的振动影响.
2 、旋转工件动力学模型
图 1 为 BTA 深孔钻削过程示意图。在加工过程中,具有一定压力的切削液流入已加工好的孔壁和钻杆外表面环形腔内,通过钻头的排屑口把切屑带入钻杆的内腔,最后流入抽屑器中。对于回转体工件的同轴孔钻削,采取工件旋转钻头进给加工方式最方便可行,这也是 BTA 钻的主要方式,可以保证孔的同轴度。钻削过程中,工件的左右两端分别固定于卡盘和导向套上,工件旋转,刀具沿轴向作进给运动。
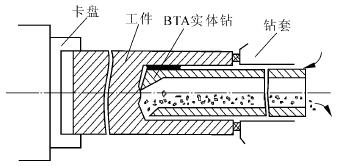
图 1 BTA 深孔钻削
图 2 为深孔钻削旋转工件动力学模型。工件在深孔钻削过程中可分为三部分: 已加工部分、正在加工部分和未加工部分,并做出以下假设和简化:
( 1) 将正在加工的部分假设为刚体,根据刚体力矩的可传递性,将径向切削力 Fy沿其作用方向从力的作用点平移到工件正在加工部分的外圆面,切削力的横坐标 L1= L - L2= Vft,其中 Vf为进给量。
( 2) 将正在加工的部分并入已加工的部分,工件由三部分简化为两部分。第一部分 B1包括正在加工的部分和已经加工的部分: 长度 L1、截面积 A1、孔径 d、截面惯性矩 I1; 第二部分 B2是未加工部分:长度 L2、截面积 A2、直径 D、截面惯性矩 I2。工件全长为 L,弹性模量为 E,密度为 ρ。
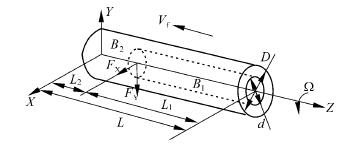
图 2 深孔钻削旋转工件动力学模型
3 、工件振动方程的建立和分析
3. 1 工件自由振动方程
设 y( x,t) 为梁横向位移量,由 Rayleigh 梁动力学方程得到图 2 所示深孔钻削旋转工件的自由振动方程,为:
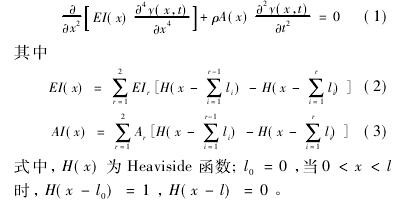

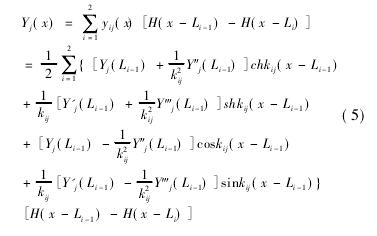
通过式( 5) 得到旋转梁第 i 段两端之间的传递关系式:


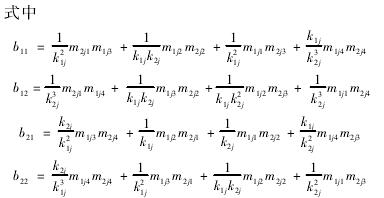




利用式( 16) 解出深孔加工中工件的横向振动坐标函数 ( x) ,并代入式( 10) 和式( 11) ,得到工件在特定加工阶段的振动偏移量。4 数值的计算及 MATLAB 拟合工件材料选用 45#钢进行分析和计算。工件长度 L = 1200mm,外径 D = 50mm,加工内孔直径 d =25mm,弹性模 量 E = 205GPa,密 度 ρ = 7. 85g / cm3,加工方式为工件旋转,刀具进给,转速为 n = 800r/min,进给量 f = 0. 15mm / r,根据文献[9]计算得到径向切削力 Fy= 1700N。
4. 1 不同加工阶段的工件振动情况
通过计算和 MATLAB 拟合可得到不同加工阶段工件的振动偏移量( 见图 3、图 4 和图 5) 。
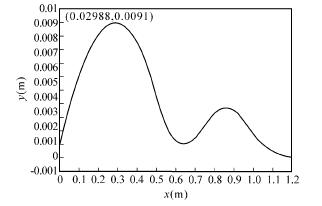
图 3 加工至 0. 3m 时工件的振动偏移量
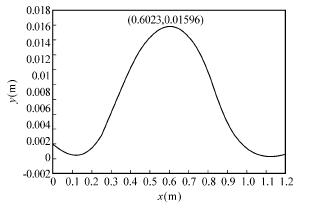
图 4 加工至 0. 6m 时工件的振动偏移量
由图可知,工件在加工时会产生径向振动,需要加装中心架对工件进行辅助支撑,降低工件的振动量,提高孔的加工精度和质量。工件在加工位置附近的振幅比较大,所以中心架的位置需要随着切削位置的改变进行适当调整。工件加工至 0. 6m 时振动偏移量最大,加工至 0. 9m 的振动偏移量大于加工至 0. 3m 时的振动偏移量,这是由于工件的质量和刚度随着加工的进行发生改变,工件的固有频率也在不断改变。
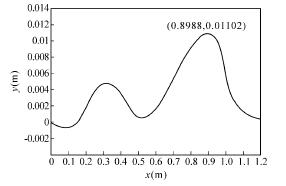
图 5 加工至 0. 9m 时工件的振动偏移量
4. 2 进给量对工件振动的影响
转速 n = 800r/min 不 变,进 给 量 分 别 取 f =0. 15mm / r、f = 0. 17mm / r 和 f = 0. 19mm / r,通过计算和 MATLAB 拟合可得到不同进给量下的工件振动偏移量( 见图 6) 。
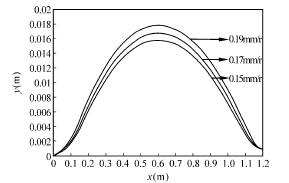
图 6 不同进给量下工件振动偏移量比较
由图 6 可知,深孔加工过程中保持工件转速不变,随着刀具进给量的增加,工件的振动偏移量会增大。
4. 3 转速对工件振动的影响
进给量 f = 0. 15mm/r 不变,转速分别取 n =800r / min、n = 1000r / min 和 n = 1200r / min,通过计算和 MATLAB 拟合可得到不同主轴下的工件振动偏移量( 见图 7) 。
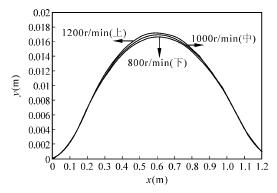
图 7 不同转速下工件振动偏移量比较
由图 7 可知,加工过程中保持刀具进给量不变,随着进主轴转速的增加,工件的振动偏移量变化极小。
5 、结语
本文针对 BTA 深孔加工中工件的振动情况进行了分析研究,运用 Rayleigh 梁理论构建旋转工件的自由振动方程,通过 MATLAB 软件分析了工件在不同加工阶段的振动情况以及主轴转速和进给量对工件的振动影响。
( 1) 工件的固有频率随着深孔加工的进行不断变化。加工位置附近的振动较大,其它位置的振动较小。在不同加工阶段,工件的振动情况各不相同,中心处的振动偏移量最大。
( 2) 进给量的变化对工件的振动会有一定影响,进给量增大会导致切削力变大,使工件的振动偏移量增大。
( 3) 主轴转速的增加对工件的振动影响极小,因为转速的提高不会导致切削力明显变化。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息




