摘要:为解决机床柔性主轴转子动平衡过程中需要在高速下试重的问题,提出一种柔性主轴转子低速无试重动平衡方法。在构建机床主轴动力学模型的基础上,根据刚体力学理论,通过对不平衡量与振动响应之间映射关系的提取,实现了工作转速下采集一次振动数据即可完成不平衡量的无试重识剐;为了在非真实失衡面对呈现柔性特征的主轴转子失衡振动进行有效抑制,分析了柔性状态下的不平衡主轴模态振动行为,并基于此提出了不平衡量校正位置迁移方法。在高速柔性电主轴动平衡平台上进行了仿真与实验分析,实验在7 200 r/min时进行,结果表明:基于一阶临界转速下所采集的振动数据,可得到迁移至两侧配重平面的等效不平衡量,对该不平衡量予以校正之后,一阶临界转速下主轴振动幅值下降了74.7%,且临界转速前后的振动降幅也较为明显,有效抑制了高速振型不平衡。
关键词:机床主轴;无试重;不平衡识别;校正位置
装备制造行业正朝着高速、高精度方向发展,这需要精准的数字装备予以支撑。数控机床是数字装备最高技术水平的载体之一,主轴系统作为现代数控机床的关键部件,其动态特性直接制约着零件制造精度[1]。由于装配工艺、变工况以及磨损等因素,主轴通常处于不平衡状态。机床主轴工作速度较高,不平衡引起的主轴振动尤为明显,这直接影响加工质量,甚至导致主轴组件损坏[2]。因此,必须采取措施控制主轴不平衡振动。
针对这一问题,国内外开展了动平衡方法的研究[3{]。动平衡是典型的已知输出求解输入的逆问题,工程中通常进行多次启停车以添加试重,从而获取转子影响系数、敏感因子等特性响应参数。然而,试重意味着自动化环节的中断,破坏了高效加工的原则,并且错误的试重更会使高速主轴运转状态急剧恶化。
能否通过最少的试重次数实现转子的高效、平稳运行,是衡量现场动平衡方法的一个重要指标。如果试重选择得当,可以实现“试重即配重”的效果,能实现这一效果的方法被称为“无试重平衡方法”[7_10]。然而,大多数无试重平衡方法通常需要在临界转速或靠近临界转速时多次获取转子振动信息,这增加了动平衡实施过程中的复杂性和风险性,也容易降低主轴系统的使用寿命。
为克服上述问题,本文结合刚体力学平衡理论,提出一种仅需在低于临界转速下对主轴采集一次振动数据,即可无试重识别主轴不平衡量的策略,进而研究了基于模态分析方法的不平衡量校正位置迁移方法,实现了在低速下对柔性主轴不平衡振动的有效抑制。
1 、不平衡量无试重求解
有限元方法在转子动力学分析中得到了广泛应用[11|。主轴有限元模型通常由离散质量圆盘、连续质量轴段以及弹性轴承座等单元组成,综合各单元运动微分方程,可得主轴系统运动方程为

若U为已知,通过式(4)可求解y。
主轴在装配之前,轴体本身的不平衡量在平衡机上经过离线动平衡后,残余不平衡量很小。然而,在主轴运转时,不平衡量仍不可忽视,且更多出现在电机绕组及刀具刀柄处。这主要是因为电机绕组结构较为复杂,高速下离心膨胀现象更为突出,其动平衡精度难以保证,而刀具在加工过程中频繁使用和更换,无论是刀具磨损还是刀具更换时的安装偏心都容易导致新的不平衡。
假设在主轴前后端轴承位置设置振动监测点,相应结点编号分别为歹、k,刀具及电机绕组两处结点编号分别为g、h。这些结点在式(4)中的关系可表达为
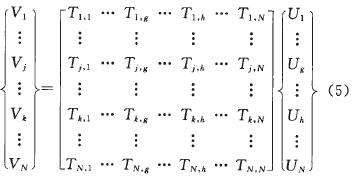
根据刚体力学理论,可将多个结点的不平衡受力等效集中至个别结点Ⅲ,通过对式(5)集中化提取处理并进行逆运算,得到刀柄接口及电机绕组位置的集中不平衡力为
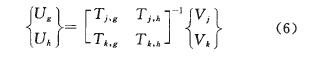
式(6)中缩减后的传递函数矩阵T已经是一个满秩矩阵,因此只需要在工作转速下采集一次振动数据,即可实现集中不平衡量的识别。
2、不平衡量校正位置迁移
尽管通过式(6)可以将主轴电机绕组及刀柄处不平衡量识别,但机床主轴内部结构较为紧凑,工业现场一般在靠近加工侧设置一个校正面,对于高精密或超高速主轴才可能配置两个校正配重面,但也通常处于主轴两侧轴承附近,而刀柄及电机绕组处不适宜施加不平衡校正量。为此,需要将J、k处不平衡校正量迁移至两侧校正面处。
若动平衡对象为刚体,仅需根据力与力偶平衡条件就可得到迁移后的等效不平衡量口]。然而,当主轴工作转速较高时,其转子将呈现一定的柔性特征,振型不平衡将被激发。此时,如果选定的等效不平衡量平面刚好处于真实不平衡量所在平面时,例如电机绕组及刀柄处,振型不平衡就能被较好地控制;如果相差位置较大,例如选定在校正面处,则校正量只能保证当前转速下测振点处的振动较小,但其他转速、位置的振动仍将受振型不平衡的影响,动平衡效果也会受到明显影响。
根据转子动力学分析[123可知,柔性转子的挠曲
艿(s)可表示为主振型之和
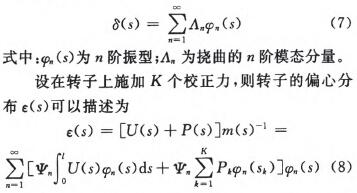
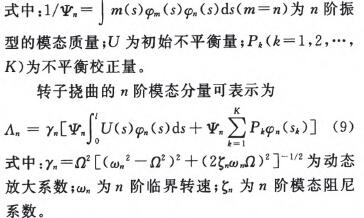
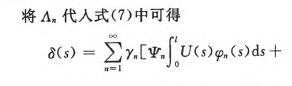

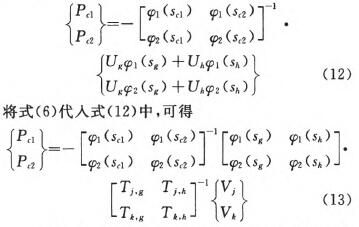
在式(13)的构建过程中引入了主轴模态振型信息,即基于该公式的不平衡量迁移方法考虑了振型不平衡的影响,从而能在非真实不平衡量所在平面实现振型不平衡的抑制。
3、实例验证
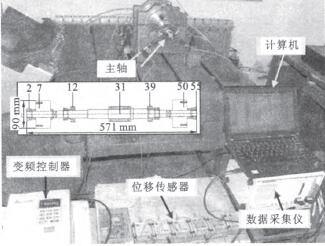
为验证所提出的机床柔性主轴转子低速无试重动平衡方法的效果,需在高速柔性主轴上进行实验。图1所示为RT—C145型电主轴动平衡验证平台,其设计最高转速约为16 000 r/rain,第一阶临界转速约为11 200 r/rain。该主轴结构上两端伸出,电机位于主轴中央,两侧分布支承轴承,两端伸出并设有校正配重盘,沿周向均匀分布24个配重孔。
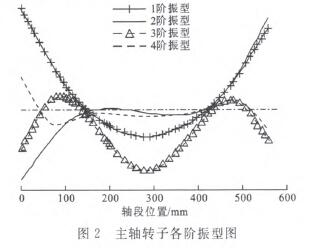
对图1所示的主轴进行有限元分析,模型共划分为55个结点,其中左、右轴承分别在第12、39结点,左、右配重校正面分别在第7、50结点,刀柄位于第2结点,电机位于第31结点。基于有限元模型可得主轴各阶振型如图2所示。
注:2、7、12、31、39、50和55为有限元模型的结点编号
图1 l机床主轴动平衡测试平台
为分析动平衡方法的有效性,在主轴模型中刀柄、电机对应结点施加的虚拟不平衡量分别为5.04g·mine35度、3.83 g·mmA一30度。以主轴工作转速7 200 r/min为动平衡测振速度,则按式(13)计算得迁移至两侧校正面上的等效不平衡量分别为6.72 g·mm么31.5度、0.64 g·mm么一20.4度。按计算结果反向加载配重,则主轴动平衡校正前后振动如图3所示。
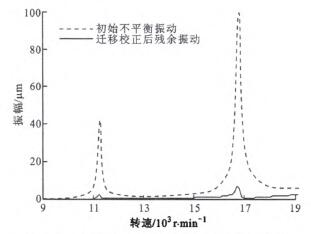
图3 7 200 r/min下动平衡前后振动仿真对比
由图3可知,当按式(13)在柔性下进行不平衡量迁移校正时,仅需在低于临界转速的状态下采集振动数据。动平衡校正之后,取得了良好的动平衡效果。在一阶临界转速下振动峰值由42.4扯m降至2.52 ttm,降幅达到94.1%;在二阶临界转速下振动峰值由98.9 ttm降至7.37扯m,降幅达到92.5%。图3分析结果验证了动平衡方法的有效性,进而在图1所示的主轴动平衡平台上进行现场实验,该主轴实测一阶临界转速约为11 320 r/min,与图3中模型计算结果11 270 r/min比较吻合,间接验证了模型的有效性。实验过程中,考虑测试点布置的便利性,振动测试点设置在主轴两端配重盘处,振动信号通过电涡流位移传感器获取,为验证低速动平衡效果,实验转速设置为7 200 r/min,即在一阶临界转速以下采集振动信号。当主轴稳定运行于7 200 r/min时开始数据采集,两端振动数据经去噪、滤波处理后,提取工频振动值代入式(13),即可求解得到迁移至两校正面上的等效不平衡量分别为20.7 g·mm么一55.1度、4.27 g·mm么一134.9度。在两端配重盘上按该求解值施加校正量后,主轴残余振动如图4所示。
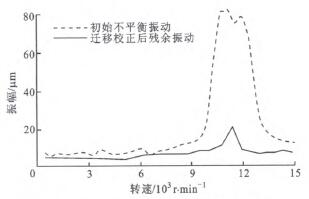
图4 7 200 r/min下动平衡前后振动实验对比
由图4可知,动平衡校正之后,在一阶临界转速下振动峰值由82.5ⅡITI降至20.9 ttm,振动幅值下降了74.7%,且临界转速前后的振动降幅也较为明显,这表明主轴转子高速下所呈现的振型不平衡被有效抑制。此外,由于该主轴有轻微各向异性特征,不同方位一阶临界转速有微小差异,从而导致图4中一阶临界转速附近的振动峰值略有波动。
图4中平衡校正后振动仍有残余,其主要原因在于:首先,实验主轴的不平衡量不可能完全分布在预估位置,这会对迁移校正过程引入一定的精度损失;其次,转轴自身存在的弯曲等非失衡故障、加工装配精度以及模型构建误差等因素也会影响动平衡效果;最后,动平衡精度还受到最小平衡配重螺钉质量所导致的配重精度偏差影响。
4、结论
本文提出了基于力学分析的机床主轴不平衡量无试重识别以及校正位置迁移方法,并通过实例验证了其有效性,主要结论如下。
(1)基于力学分析的主轴不平衡量识别方法可以实现对不平衡量的无试重辨识,且识别过程仅需在工作转速下采集振动数据。
(2)不平衡量校正位置迁移方法可将识别不平衡量从其真实分布平面等效迁移至校正平面。
(3)考虑振型信息的柔性主轴不平衡量校正位置迁移方法可有效抑制机床主轴高速振型不平衡。此外,基于模型的无试重动平衡方法能否应用于工业现场,其关键在于动力学模型及参数能否准确反映实际主轴转子的真实情况。因此,在构建动力学模型时,一方面要采用合理的方式分析主轴动力学行为,另一方面要结合实验手段,对所构建的模
型进行修正,实现对主轴振动行为的准确描述,减少由于非主轴自身预期特征所导致的误差。
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com




