一种航空发动机整体叶盘在线检测新技术
2014-3-18 来源:数控机床市场网 作者:黄进 汪洋 马孜 刘滨春
摘要: 为了解决航空发动机整体叶盘的在线检测问题, 提出了一种工业机器人整体叶盘在线检测系统. 该系统以工业机器人为主执行器, 携带具有通信功能的电子杠杆表采集检测数据. 整体叶盘被装卡在外部旋转轴上, 通过旋转定位实现整体叶盘各个盘叶的检测. 系统工作前需要对机器人、 电子杠杆表以及外部旋转轴的空间位置关系进行标定, 并通过空间坐标系转换实现整体叶盘检测数据的还原. 实验结果表明: 该系统能够对整体叶盘的各项参数实现在线检测,整体检测精度达到 ? 0?05mm. 与传统整体叶盘检测方法相比较, 在保证精度的前提下, 该系统工作更为柔性高效, 并且更加适合加工现场的在线检测要求.
关键词: 航空发动机整体叶盘; 机器人; 检测
整体叶盘是现代航空引擎比较新的结构主件, 对提高飞机发动机的性能至关重要. 然而, 由于整体叶盘型面复杂检测比较困难. 整体叶盘检测的常规手段是利用三坐标测量机携带接触或非接触测头在叶盘上进行逐点或逐线测量. 接触测头必需接触到待测的每个点, 因此测量速度比较慢. 非接触测头的测量速度虽然较快, 但是对于刚加工后叶盘的光亮表面则不能直接测量, 必须在叶盘表面喷显影剂后才能进一步检测. 这样的处理不但浪费时间, 还会将不均匀的喷涂误差带入测量, 而且不能实现在线测量. 因此, 需要更柔性的方案来解决以上问题.随着工业机器人精度和可靠性的提高, 将其用作为三维扫描和检测的运动执行器成为可能. 电子杠杆表测量头可以与工业机器人配合能够伸入整体叶盘工件的狭窄和较深盘叶间隙中进行测量.
测量数据和机器人位姿数据可以通过电子杠杆表和机器人的数据通信串口传入上位计算机实现连续测量. 这种测量方式可以对整体叶盘的所有位置进行检测.
1 系统运动模型
1 . 1 系统坐标系定义
如图 1所示, 系统包括一个六自由度机器人, 在其手腕法兰上固定一个电子杠杆表. 整体叶盘固定在一旋转工作台上.
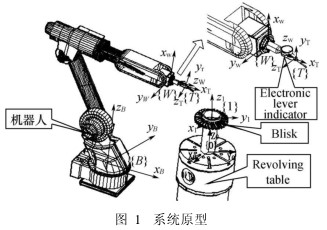
在测量空间上定义 5个坐标系, 分别为: 基础坐标系 {B}, 位于机器人底部旋转中心; 手腕坐标系{W}, 位于机器人运动终端的法兰中心; 工具坐标系 {T}, 位于杠杆表转轴处; 坐标系 {0}, 位于转台工作面; 坐标系 {1}, 位于待测整体叶盘基准面.
1 . 2 杠杆表标定
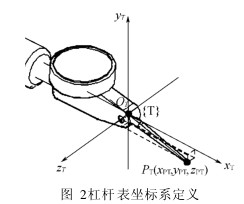
图 2显示了杠杆表坐标系的定义. 工具坐标系 {T}中的 ZT 轴与转轴同轴; 原点 OT在表杆延伸轴线与ZT 轴的交点处; XT轴与杠杆表底基准面平行. 杠杆表一般用于测量表面微小的相对变化, 应用时只关注表杆与测量面的夹角. 如果夹角大于 10 , 为避免误差太大则测量数据必需乘上修正系数. 而其他因素, 如ZPT, YPT一般不用考虑. 然而, 在这个应用中杠杆表的位姿随着机器人的手腕不断变化. 因此初始坐标值PT0(XPT0, YPT0, ZPT0)必需要精确地标定出来. 在工具坐标系 {T}中 PT(XPT, YPT, ZPT)可以表示为

式中, L 为杠杆表触测球头中心到原点的长度; v 为杠杆表的读数; α为表杆与被测量面的夹角; Δθ为表杆绕 ZT旋转的角度.
1 . 3 腕到工具坐标系的标定
为了将测量数据转换到基座标系下, 首先需要将杠杆表所在的工具坐标系 {T}下获得的数据转换到腕坐标系 {W}下; 然后根据腕坐标系 {W}相对于基座标系 {B}的位姿变换将测量数据转换到极坐标系下.系统的联合变换可以表述为
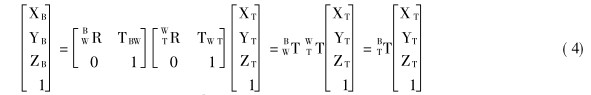
式中, PB (XBYBZB )表示 {B }坐标系下任意一点;BwR 代表从腕系 {W}到基系 {B}的旋转变换矩阵; TW B为在基系 {B}下腕系 {W}原点的平移向量;WTR 为从工具系 {T}到腕系 {W }间旋转变换矩阵; TWT在腕系 {W}下工具系 {T}原点的平移向量. 利用最小二程法或其他的优化算法可以获得更好的标定结果.
1 . 4 基坐标系到工作台坐标系的标定
此标定的主要目的是确定基系 {B}到工作台坐标系 {0}的转换关系. 标定过程需要将一个标准球固定在工作台上, 并随工作台按标定程序旋转. 测量机器人在均匀对称位置采集数据, 并利用式 ( 4)计算出相对于基系的采样点数据. 球心点 ( xi, yi, zi)的运动轨迹在同一圆周上. 旋转轴向量 V0可以由下式计算:
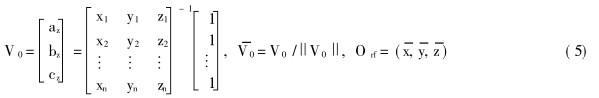
式中, Orf为采样点的平均值, 可以作为参考坐标系 {R}的原点,

圆轨迹上的点可以通过下式将基系 {B}的值转换到旋转工作台系 {0}:

由于在 P0i的所有的点都基本在同一平面上, Z0i可以看作 0 , 并在转换后忽略, 只关心 (x0i, y0i). 可以利用最小二乘圆算法来确定圆心坐标 (A, B). 这个圆心坐标代表 {R}系的原点, 用以下算式计算出其在基系 {B}下的值:

经过以上的标定计算, 在 {B}系下的 {0}系原点可以计算出来, 其传递矩阵为

整体叶盘用卡具固定在旋转工作台上, 其基面与旋转工作台平行, 距离 z01可以直接测量, 其中心与工作台旋转轴同轴. 整体叶盘所在坐标系 {1}相对于 {0}系的传递矩阵为

如果测量值 PT和工作台转角 ? 1已知, 则可以通过以下算式计算出叶盘的整体数据:
2 试验结果

实验系统如图 3所示, 包括一台 M otom an HP3机器人, 一个SYLVAC电子杠杆表 (量程 13mm, 分辨率 0.001mm ), 一台外部旋转工作台和一件整体叶盘.
实验步骤如下:
① 标定电子杠杆表.
② 标定腕系 {W}到工具系 {T}间的传递矩阵. 获得的标定结果为

③ 标定基系 {B }到旋转工作台系件的传递矩阵. 获得的标定结果为

④ 固定整体叶盘到卡具上. 测量整体叶盘基面到旋转工作台 {0}系原点的距离确定矩阵 {1}相对于矩阵 {0}的传递矩阵为
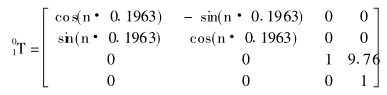
式中, n 为叶盘序号.
⑤ 移动杠杆表到起始测量位置, 按测量顺序要求进行测量, 用式 ( 11)计算叶盘相对于坐标系 { 1}的数值, 直至完成本叶片的测量.
⑥ 旋转工作台到下一叶片.
⑦ 回到步骤? 直至完成所有叶片的测量.
⑧ 利用球头补偿算法补偿测量数据获得最终测量结果.
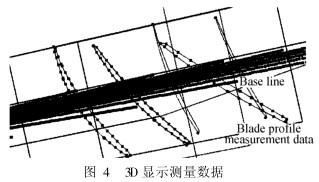
图 4显示了在一个叶片上测量的 3条测量轮廓线, 用标准块对系统的测量精度进行了验证, 结果表明平均误差为 0.05mm.
3 结语
本文主要就整个系统运动模型的建立, 杠杆表工具坐标系模型建立和标定, 工具坐标系与机器人手腕坐标系的标定以及机器人基坐标系与工作转台坐标系的标定问题进行了探讨, 建立了原型机实验系统, 并获得了比较满意的实验数据, 从而验证了此新方法的有效性.
实验表明该系统虽然能够在现有条件下完成整体叶盘的在线检测, 但要想达到实用水平还需要进一步提高系统各硬件设备的精度. 未来的进一步工作主要集中在如何使系统更加实用可靠, 硬件升级以进一步提高系统的测量精度, 完善软件功能以适应整体叶盘加工在线检测实际需求.
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com




