基于装配的卧式加工中心精度建模与分析
2017-12-13 来源:大连大学 机械工程学院 作者: 李玉光
摘要:以多体系统理论为核心,运用齐次坐标变换对卧式加工中心的精度问题进行了系统、全面的分析,重点立足于装配中的精度建模和误差分析。 通过对加工中心精度建模的研究,揭示了利用齐次矩阵变换将误差从机床部件传递到被加工零件的建模方法,并对这一方法进行总结,使其具有通用性和方便性。 最后通过对某加工中心进行实例分析,验证了方法的可行性。
关键词:加工中心;多体系统理论;齐次坐标;精度建模
随着现代机械制造技术的飞速发展, 精密和超精密加工技术成为现代机械制造业的发展趋势[1]。 数控机床精度一直是影响其质量的核心问题, 也是衡量机床水平的关键参数。因此,数控机床精度的研究受到了广大学者的关注。 我国目前的机床加工水平较世界发达国家还存在一定的差距 ,提高我国数控机床的加工质量, 研究数控机床的精度问题已成为一个重要的研究课题。
目前, 我国生产的数控机床约占国内市场份额的50%左右, 中高端数控机床市场的绝大部分被境外产品占领, 其中高端数控机床国内产品的市场占有率仅4%左右[2]。 造成这种现象的主要原因是国产数控机床的性能、加工精度、稳定性和可靠性等方面都难以与国外高档产品相比, 其中加工精度是国产数控机床的主要薄弱环节。
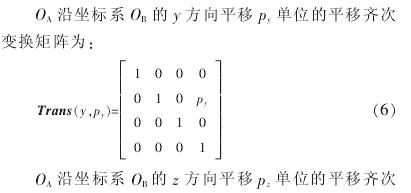
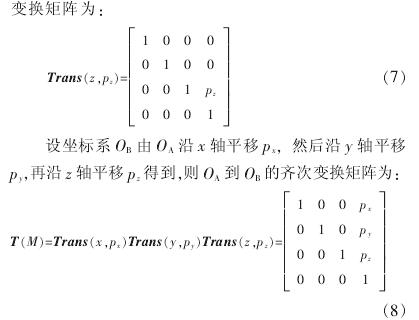
由于机床误差而导致加工精度下降的问题日益突出,如何对机床误差进行建模,进而补偿甚至消除误差成为一项重要的研究任务。
1 、误差建模概述
机床精度在设计阶段取决于两个因素, 一是零件的加工误差,通过公差设计的控制可以减小加工误差;二是装配工艺,在装配过程中会积累误差。因此保障机床的精度,必须从公差分析和装配偏差入手,建立几何精度表达和传递的数学模型[3]。
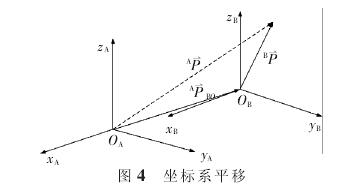
这样可以对整机的装配进行预测,从而保证数控机床的加工精度。文中以卧式加工中心为例, 如图 1 所示, 其几何精度要求很严格,在微米范围内。 考虑到生产的成本,不可能仅通过高水平的制造能力提升公差要求来确保数控机床的装配精度。
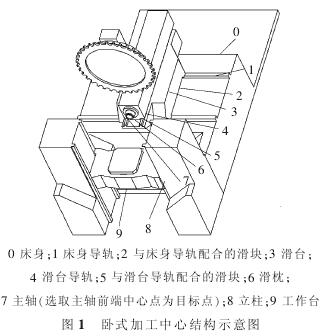
因此,在实际机床装配过程中,一般会采用测量和调整的手段来减小误差。 状态空间模型是一种描述装配偏差传递的有效方法[4]。
加工中心主要由床身、立柱、主轴、各种直线导轨和回转轴组成。其中每一部分都会由其本身的加工、装配、运动及发热等产生误差。 当一部件沿导轨运动时,将产生 6 个自由度的误差, 这些误差项通过机床运动的传递和变换构成几何误差,此,精确地建立机床空间误差十分重要。 目前机床误差的理论建模技术主要有基于运动学模型、基于多项式模型等。
在基于运动学模型的误差建模技术方面:D L Leete 等于1961 年首先利用三角关系建立了三轴机床的几何误差模型[5];Schultschik 于 1977 年利用矢量表达方法分析三轴锉床的空间误差分量[6];Ehmann 等于 1993 年提出了一种直接空间误差分析法[7];Kiridena 等用机构学方法建立五轴机床的空间误差模型[8];Eung-Suk Lee 等于 1998年对三坐标铣床 21 项误差进行了测量,通过误差合成法建立空间误差模型[9]。
近几年来也出现了很多其他建模方法:杨建国在 1998 年利用齐次矩阵变换原理建立了车削加工中心的几何与热误差 综合模型[10 -11 ];Rahman 等于 2000 年同样基于齐次坐标矩阵建立了多轴数控机床的准静态误差综合空间误差模型[12];Bohez等于 2011 年以将机床运动部件简化为刚体为前提对五轴机床进行了误差补偿[13]。
因此, 多轴数控机加工系统的误差分析和补偿问题一直备受国内外专家关注, 也一直是学者们研究的热点。但是目前为止还未有一种系统性、完整性和通用性的建模方法。近几年,为了解决复杂机械系统的误差分析,多体系统理论应运而生。多体系统理论可以对复杂的多轴机床进行系统性描述, 同时能够综合考虑影响系统的多项因素,因此被广泛适用于复杂机械系统的建模[14]中。
由床身、立柱、主轴、刀架、刀具和回转轴部件等构成的机床,从本质上看就是一个复杂机械系统,因此非常适合采用多体系统理论进行研究。然而,目前大多数的研究依然停留在理论模型的分析上。 文中则从实际机床产品的加工中心出发, 应用多体系统理论得到一般机床的精度建模方法, 并利用这一方法对具体实例进行分析,验证了方法的可行性
。
2 、多体系统理论
多体系统理论广泛应用于船舶、航空、车辆、通用机械等产品的设计和试验[15],它涵盖建模和求解两个阶段, 建模阶段包括从几何模型形成物理模型的物理建模、由物理模型形成数学模型的数学建模两个过程;求解阶段需要根据求解类型选择相应的求解器进行数值运算和求解。
利用多体系统理论对图 1 所示的加工中心精度进行分析,提出了一种符合实际的分析方法。这种方法采用齐次矩阵来表示空间中点的位置和矢量的姿态,用4×4 阶齐次方阵(传递矩阵)对在理想条件下和实际条件下静止状态时物体间的相对位置和姿态进行分析;通过方阵之间的运算,使得多体系统的分析变得简单、清楚,为实现计算机快速建模提供基础[16]。
2.1 空间物体的位姿描述
任意两个零件装配时, 都会在 6 个自由度方向上产生误差,这一误差称为静止误差。 相对运动时,也会在 6 个自由度方向上产生误差, 这一误差称为运动误差。 以 x 轴方向平动为例进行分析,6 项误差如图 2所示。
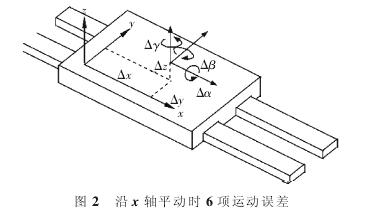
2.1.1 旋转运动齐次特征矩阵
在各种形式的旋转运动中,把分别绕坐标轴 x,y,z的转动看成基本转动,如图 3 所示,其他复杂的转动形式都可以由这 3 种基本转动得到。为方便研究,将复杂的旋转分解到绕坐标轴 x,y,z 的 3 种基本旋转运动来研究。
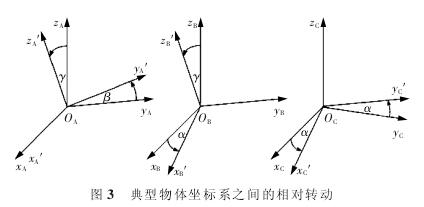


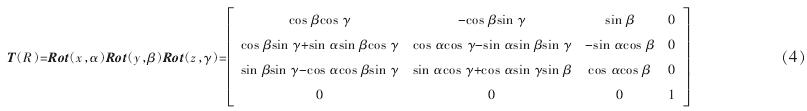


3 、卧式加工中心精度建模实例
数控机床是一种典型的多体系统,传统方法显现了很大的局限性,如需要较严格的假设条件,造成分析计算结果与客观事实相差较大。 因此用多体系统理论解决数控机床的运动学问题是适用于数控机床研究需求的。 文中以第 2 节的理论为基础,根据多轴数控机床的拓扑结构,利用齐次特征矩阵来对加工中心进行建模。
图 1 所示的卧式加工中心中,滑枕与滑台的配合、滑台与床身、立柱的配合实现 3 个方向的运动,使得加工中心有很大的加工范围。 选取产生切削力的轴线方向为 z 轴方向, 同时规定刀具远离工件的方向作为 z轴的正方向;x 轴则位于与工件安装面相平行的平面内且垂直与 z 轴, 向右为 x 轴的正方向;y 轴与 x 和 z轴垂直,向上为 y 轴的正方向。
3.1 机床的拓扑结构
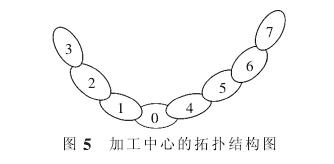
加工中心精度建模的实质是要找到工件和刀具的相对位置。因此从卧式加工中心的床身出发,分别沿刀具方向和工件方向建立拓扑模型。沿工件方向:设床身为 0 号件,立柱为 1 号件,滑板为 2 号件,工作台为 3号件;沿刀具的方向:设床身为 0 号件,滑台为 4 号件,滑枕为 5 号件,主轴为 6 号件,刀具为 7 号件。 根据相关拓扑理论[17],对卧式加工中心的主要零件进行拓扑 ,其拓扑结构如图 5 所示。
3.2 基于装配的精度模型分析
一般情况下各个零部件之间的装配误差可以通过实测得出,然后将误差数据代入精度模型中进行分析。文中加工中心的很多因素还在论证和修改阶段, 因此无法进行装配实际数据的提。 通过查阅大量的文献及获取厂方装配过程所能达到的精度, 通过对装配误差赋值,得到了装配误差的一组假设值,并基于此对精度函数进行计算。 假设值如表 1 所示。
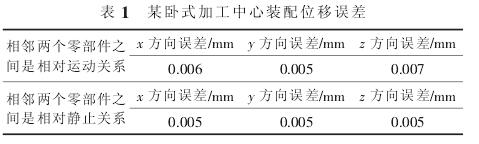
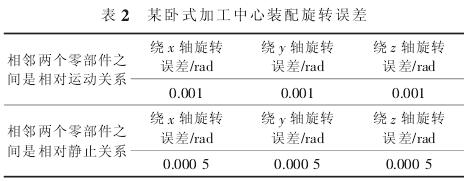
在装配时, 旋转误差值通常在相对运动的部件间比在相对静止的部件间大一个数量级。 假设值如表 2所示。
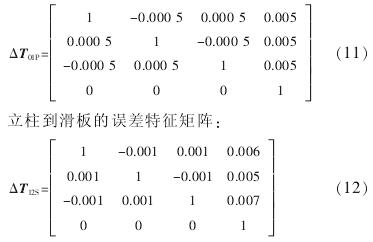
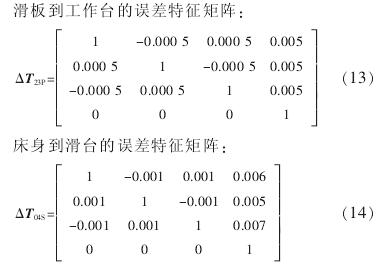
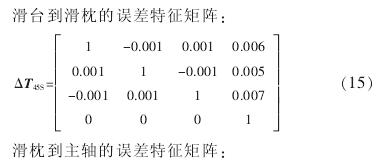
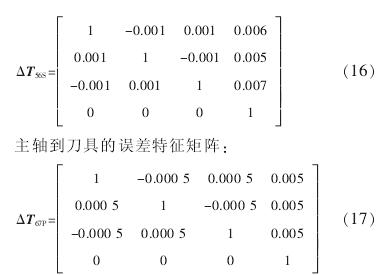
将以上数据进行整理,代到误差特征矩阵中有:床身到立柱的误差特征矩阵:

4 、结论
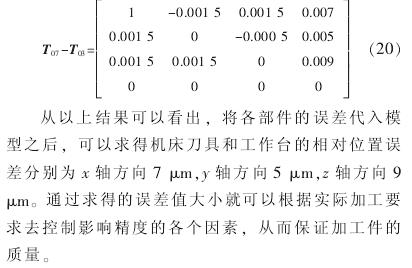
首先对多体系统理论进行分析, 利用齐次变换矩阵, 通过平移和旋转后的变换矩阵总结出具有通用性的多轴数控机床精度建模方法; 再通过对某卧式加工中心的具体实例进行分析,结合相关文献及经验,对误差值进行取值并代入建立的误差模型, 计算出刀具与工作台之间的相对位置误差。 这样可以根据具体的加工要求合理地控制关键位置的相对误差, 为误差建模提供了一种有效的方法。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息





