宏程序在高次曲线加工中的应用
2018-4-18 来源:福建水利电力职业技术学院 作者:兰嵩
摘要:虽然各种各样的自动编程软件层出不穷,但手工编程仍有它不可替代的地方。本文基于FANUC-0i-mate数控系统B类宏程序的编程指令,有条理地分析了在编制高次非圆曲线时遇到的困难以及解决问题的方法,为宏程序其他场合的应用提供了思路。
关键词:数控机床;宏程序;高次非圆曲线
随着产品的不断改进,机械零件的轮廓不再是只由直线段和圆弧段构成,出现了二次非圆曲线包括椭圆、双曲线、抛物线、正弦曲线等。如果用自动编程软件编程,会出现程序可读性差、程序冗繁、程序灵活性不够好等缺陷,而宏程序就能克服这些缺陷。
1、问题提出
数控系统通过准备功能指令 G 代码控制数控车床的移动部件 (刀架) 运动。在 G 代码中,能够使得车床动作的指令有 G01 直线插补、G02 顺时针圆弧插补、G03 逆时针圆弧插补,以及其它循环功能指令。但是,无论使用哪个 G 代码,刀架的运动轨迹从肉眼上看去走出的是直线或者圆弧。
从原理上对运动控制进行分析:数控系统是按照插补算法来控制移动部件运动,不同的插补算法走出的轨迹是不一样的,但都是通过折线来逼近直线或圆弧 (见图 1 和图 2)。我们把数控系统统发送一个脉冲,机床移动部件运动的距离称为脉冲当量,可达到 1μm。因此,逼近的折线几乎就是直线或圆弧,能够达到零件轮廓精度的要求。
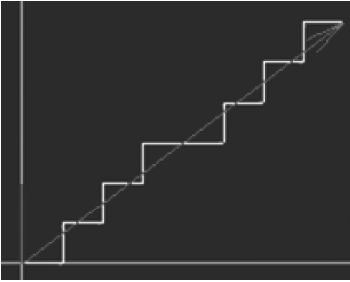
图1 逐点比较插补法
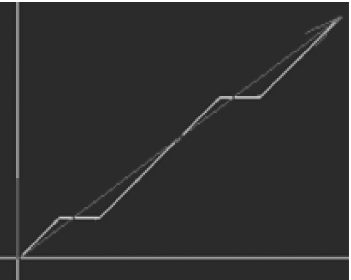
图2 数字积分插补法
遇到走刀轨迹是非圆高次曲线,我们可以参考上述插补原理,采用将曲线分割成若干条直线段来逼近 (见图3)。而要让数控系统控制刀架走出一段直线,编程人员需要计算出直线段的终点坐标值、编写一行程序来实现。如果分割的线段越少,编程的计算量就大大减少、程序简洁,但是零件的加工精度无法保证;反之,分割的线段越密集,确实能够保证加工精度,但缺点是坐标的计算量大,程序冗繁。因此,如何利用系统自动计算坐标和简化程序这两个问题需要我们解决。
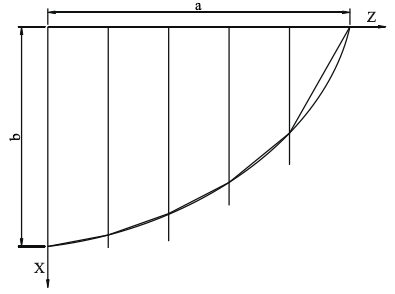
图3 折线逼近椭圆
2、问题解决
2.1 坐标计算
如果将曲线分割成 10000 段,我们就需要计算 10000 个点的坐标值。如果只靠人工计算,工作的效率太低,且容易出现错误。目前大多数数控系统都有提供宏程序功能,与普通的数控程序相比较更具有灵活性。在宏程序中,字可以使用变量,通过让变量执行赋值、运算等操作来控制机床移动部件走出有规律的轨迹。宏程序有 A 类和B 类两种,FANUC-0i- mate 系统常采用B 类宏程序进行编程,下面我们将说明如何利用 B 类宏程序解决坐标计算问题。
2.1.1 变量
1) 变量表达:一个变量可用#K (K=1,2,3……) 来表达,如#28。2) 变量分类:系统提供了三种变量,全局变量、局部变量和系统变量。
2.1.2 变量运算
变量运算包括赋值数学运算和函数运算。
1) 赋值使用符号“=”,作用是将“=”右边的数值存放至“=”左边的变量中。
例如:#28=50。
2) 数值运算符号包括“+、-、*、/”,可以数值和数值间运算,也可以数值和变量间运算,还可以变量和变量间运算。例如:#28=#29*#30,含义为将变量#29 中存放的数值和变量#30中存放的数值相乘,得到的结果存放在变量#28中。
3) 常用的函数运算符号有:
SQRT (平方根)、ABS (绝对值)、SIN (正弦)、COS (余弦)、TAN (正切)、ATAN (余切) 等。例如:#28=SQRT[#29],含义为将变量#29 中存放的数值开平方根,得到的结果存放在变量#28
中。
2.1.3 运用宏程序解决坐标计算
假设要控制机床移动部件走出椭圆轨迹,已知椭圆的长半轴为a,短半轴为b,我们可以得到轨迹的方程为相比较更具有灵活性。在宏程序中,字可以使用
变量,通过让变量执行赋值、运算等操作来控制机床移动部件走出有规律的轨迹。宏程序有 A 类和B 类两种,FANUC-0i- mate 系统常采用B 类宏程序进行编程,下面我们将说明如何利用 B 类宏程序解决坐标计算问题。
2.1.1 变量
1) 变量表达:一个变量可用#K (K=1,2,3……) 来表达,如#28。
2) 变量分类:系统提供了三种变量,全局变量、局部变量和系统变量。
Z2/ a2+ X2/ b2=1 (1)因此,我们可以得到 X 坐标关于 Z 坐标的方程:

表1 变量类型
X =baa?a - Z?Z (2)当给定轨迹上某个点M的Zm坐标值,就能通过上面的公式计算出该点的Xm坐标,而这个运算过程可以让数控系统的宏程序来实现。我们选用#100和#101两个变量,用#100来存放Xm坐标,用#101来存放Zm坐标,因此得到:#101=Zm;(将M点的Z坐标存放到#101)#100=b/a*SQRT[a*a-#101*#101];(计算出 M点X坐标)G01 X#100 Z#101 F0.2;(运动到该点)
2.2 程序简化
移动部件从轨迹起点运动到终点,Z 坐标 Z2则从 a 连续变化到 0。如果将轨迹分割成 1000段,则赋值、计算和运动各需要 1000 行程序段,因此程序非常冗繁。要解决这个问题,需要用到程序的控制指令功能。

表2 条件式格式
2.2.2 程序跳转语句
1) IF<条件式>=GOTO n (n为程序段号)当<条件式>成立时,程序跳转到段号为 n 的程序段往下执行;当<条件式>不成立时,程序不执行跳转,继续往下执行。
2) WHILE< 条 件 式 >DO m (m=1, 2,3……)……END m当<条件式>成立时,程序重复执行 DO m 到END m 之间的程序,直到<条件式>不成立;当<条件式>不成立时,程序从 END m 这一段往下执行。
3) 两种方法比较用IF语句控制程序跳转时,系统必须从程序头开始逐段扫描程序段号,直到符合语句中的段号 n 时 , 才 开 始 执 行 程 序 , 效 率 较 低 ; 而 用WHILE 语句时,系统只需循环 DO m 到 END m 之间的程序,效率高。因此推荐使用WHILE语句进行控制。
2.2.3 程序编制取变量
#102 存放 Z 方向递减的步长。Z 坐标从轨迹起点 a 开始,每次递减步长,计算出轨迹上新点的 X 坐标,控制刀具运动到新点。系统重复以上步骤,直到刀具运动到轨迹终点,从而走出曲线轮廓。轮廓加工的精度取决于步长值的大小,步长越小,轨迹被分割成的线段就越多,那么与轮廓的相似度就越高。设置椭圆圆心为编程原点,加工的宏程序如下:

从上面程序我们可以看出:采用宏程序编程,不仅能够简化编程结构,并且对提高编程和加工的效率也有重要的作用。
3 、宏程序的其他应用
数控机床的编程方式包括手工编程和自动编程,随着各种各样的编程软件不断出现,大大提高了编程效率,但在某些场合中并不能完全取代手工编程。手工编程,特别是宏程序编程仍具有自己的优势。
1) 通过改变对变量赋值,可以加工不同尺寸但形状类似的零件。例如需加工多个不同零件,每个零件上都有椭圆轮廓,但尺寸、椭圆圆心与编程原点相对位置不同。我们可以先确定出椭圆的非标准式方程 (通式),编制椭圆宏程序并作为一个子程序,然后根据要加工椭圆的参数将方程中的所有常数 (包括:长半轴、短半轴、起点坐标、终点坐标、椭圆圆心相对编程原点的距离、步长等) 赋值给变量,最后用调用子程序的方法走出轨迹。
2) 数控系统中有专门用来存放刀具补偿的变量,可以解决因刀具磨损造成的精度误差。当加工多个零件后,刀具会产生磨损,若使用原有的程序继续加工,那么零件的尺寸会超出公差允许范围。这时,我们只要在程序中加一行将刀具磨损的值赋给磨耗变量的程序段,使得刀具轨迹偏离一个磨损量,就能够保证加工合格。除此之外,宏程序还在其他场合广泛使用。比如特殊螺纹的加工、用同一个程序进行粗精加工等。
4、结束语
宏程序和普通程序相比较最主要的区别在于宏程序可以使用变量,并给变量赋值,变量之间可以进行运算,程序可以控制跳转;而普通程序中只能使用常量,常量之间不能运算,程序只能按顺序执行。做为一名优秀的数控编程人员,不能只会使用CAD/CAM软件出后置处理程序,要根据企业的实际情况合理地选择程序编制方法。因此,掌握宏程序的编制方法是非常有必要的。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息




