精密研抛数控机床几何误差与热误差复合建模及其补偿研究
2016-11-10 来源:长春工业大学 作者:张恩忠,李刚,林洁琼,冉同欢
摘要:为了提高精密研抛数控机床的加工精度,对研抛数控机床的几何误差与热误差进行了研究与分析,发现随着机床相关部件温度的不断升高直至热稳态,机床的定位误差也不断增加到稳态值,验证了几何误差和热误差是精密及超精密加工误差的主要来源。综合考虑了机床复合误差的不同特点并进行误差分离,提出了基于牛顿插值算法和最小二乘法的几何与热复合误差建模方法,依据复合误差模型进行补偿实验, 补偿后机床冷态下定位误差值从3. 5μm 降至1. 2μm, 误差降低了65. 7%,热稳态后定位误差值从12. 2μm 降至1. 9μm,误差降低了84. 4%,实验结果证明复合误差模型计算简单、预测精度高、具有较好的鲁棒性,为提高机床的加工精度提供了理论与实践依据。
关键词:研抛数控机床;插值算法;复合误差模型;误差补偿
0.引言
由机床本身制造、装配精度引起的几何误差和由机床在加工过程中热变形引起的热误差是影响数控加工精度的关键因素。在精密、超精密加工中,数控机床的几何误差和热误差约占总误差的70% [1-2] ,其中热误差是影响机床加工精度的主要因素。数控机床热误差形成的原因多种多样,其中包括机床所处的加工环境、机床上各种热源影响、人为造成的因素等,国内外学者对数控误差建模和补偿方法进行了广泛研究,文献[3]赵帼娟等建立了四轴抛光平台的综合误差模型并分析其误差的主要来源、文献[4]韩飞飞等对数控机床的几何精度进行了综合分析,并验证了定位误差是影响机床几何误差最主要的因素、文献[5]重点研究了机床表面的轮廓误差与几何误差之间的耦合关系并进一步分析与研究了机床导轨的精度,虽然上述都考虑了几何误差的影响,但都忽略了热引起的误差因素。相关学者对热误差建模方法做了大量的研究,其中包括基于支持最小二乘向量机[6] 、模糊神经网络[7] 、灰色理论[8] 、回归分析[9] 等,虽然这些误差建模方法的预测精度较高,但在实践操作过程中还存在建模方法较复杂且时间较长,模型鲁棒性较低等一些缺点。
本文在一台自主搭建的精密研抛数控机床上进行试验与研究,综合考虑了不同温度状态下机床定位误差的变化规律与相互关系,根据几何误差与热误差的不同特点进行误差分离,基于牛顿插值算法和最小二乘法对机床分别建模,再综合可得到几何与热的复合误差数学模型,通过补偿实验验证了该模型计算简便,拟合精度高,易于程序设计,为提高机床的加工精度提供了理论依据。
1.研抛机床复合元素建模原理与测量
1. 1 复合误差建模原理
复合误差是指与机床温度和位置坐标都相关的误差元素。复合误差建模过程比较复杂,先要进行几何误差与热误差的分离(如图1 所示),然后再对几何误差和热误差分别建模。采用位置K 的多项式拟合得到机床冷态下的几何误差模型,机床不同时间的热误差元素与机床温度相关,对不同时间的各热误差曲线进行一次拟合得到相应斜率,依据各时间段的温度、斜率值构造热误差模型,最后将以上两种误差模型合成为一个复合误差模型。

图1 复合误差分离图
与机床温度和位置坐标都有关的复合误差元素可表达为:

1. 2 复合误差元素测量
为了测量机床y 轴不同时刻的定位误差和温度变化值,如图2 所示,选用铂电阻式Pt100 温度传感器和16 通道的XSR90 彩色无纸记入仪进行温度测量,根据相关性分析[11] ,温度传感器T1、T2、T3、T4 分别放在机床的y 轴平台上,T1、T2 用来测量y 轴动导轨和直线电机动子的温度,T3、T4 用来测量y 轴定导轨和直线电机定子的温度,首先记入机床冷态时y 轴各测量部件的温度值,然后每隔20、40、6090、120、及150min 记入其温度变化值。

图2 温度与误差测量现场

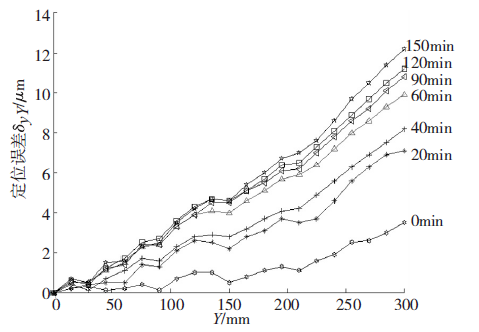
图3 不同时段的定位误差
图3 为机床不同时刻的七条定位误差曲线,从图3 中可以看出,机床y 轴的定位误差随着机床温度上升而增大,图中七条定位误差曲线形状的变化规律基本一致,只是各条曲线的斜率随机床y 轴温度的升高而不断变大,即机床在不同温度下的定位误差可以看成是机床冷态下定位误差绕机床坐标原点旋转一定角度而来,这一规律为式(1)复合误差建模提供了理论依据。
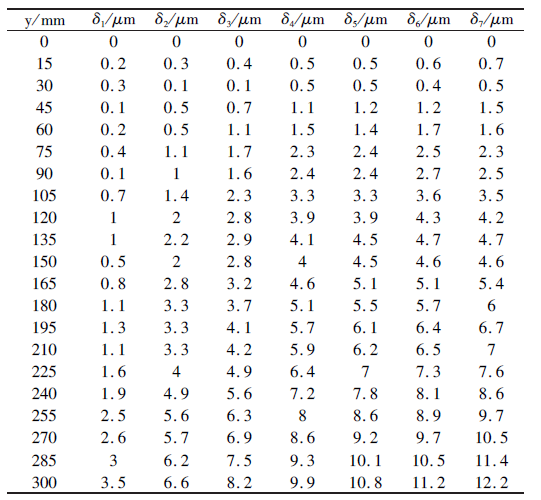
表1 所列δ1 、δ2 、δ3 、δ4 、δ5 、δ6 、δ7 为机床从冷态时至达到热稳态时7 个阶段的定位误差值,由表1 和图3中看出前3 个时间段机床误差上升较快,常温下机床的最大定位误差值与达到热平衡状态的最大定位误差值相差大约为9μm,这说明研抛数控机床定位误差受热影响较大。
表1 定位误差测量值
2.研抛机床复合元素建模
2. 1 几何误差建模
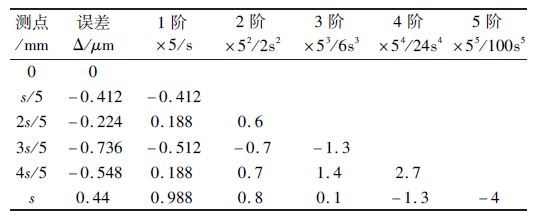
由复合误差建模原理分析可知,热引起的误差与误差曲线的斜率和机床坐标位置有关,所以几何误差和热误差建模的时候首先将机床冷态时的误差曲线旋转为水平位置(如图4 所示),然后对旋转后的误差进行几何建模,本文对旋转后的误差采用牛顿插值法进行几何误差建模,运用激光干涉仪测量研抛机床定位误差,y 轴行程为s = 300mm,测量间隔为15mm,每次测得21 个测量点,应用牛顿插值法,每隔4 个测量点选取定位误差,选取冷态下(0min)6 个(机床原点误差为0)误差值Δ(旋转后)与坐标位置构造5 阶均差,均差表如表2 所示。
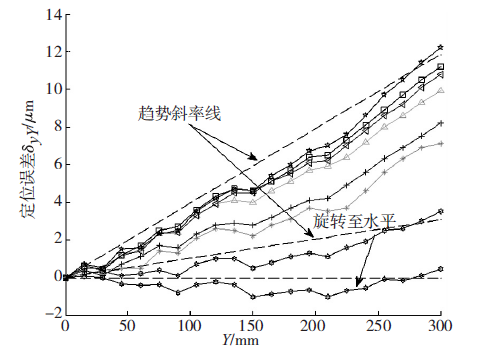
图4 Y 轴误差旋转
表2 均差表

2. 2 热误差建模
对图4 所示的7 条误差曲线进行一次拟合,可以得到不同温度下的趋势线斜率。根据相关性分析,机床y 轴电机动子和动导轨温度对y 轴误差影响比较大,所以选取这两个测温点进行y 轴热误差建模。机床不同时间下的温度测量值与各条误差曲线的趋势线斜率值的对应关系如表3 所示。
表3 温度与斜率统计表

将旋转后的几何误差模型式(3)以及热误差趋势线模型式(6)代入到式(1)可得y 向几何误差与热误差的复合模型为:

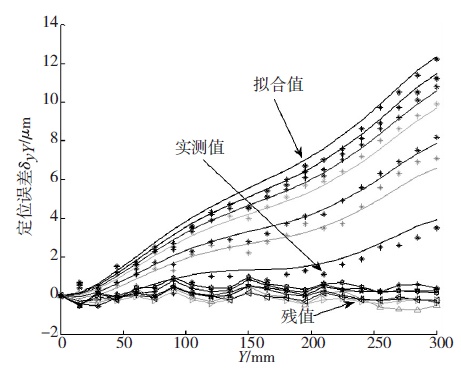
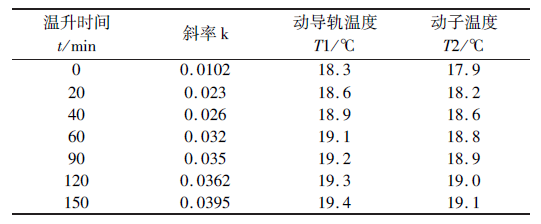
图5 Y 轴误差拟合
3.误差补偿实验
提高机床精度的方法有两种[10] ,分别为误差补偿法和误差防止法,误差防止法是试图通过提高机床本身的设计、制造和装配等精度来尽可能的减少误差来源,误差补偿法是人为地造出一种新的补偿去抵消机床原始的误差,误差补偿法相比误差防止法费用低、效率高,是提高数控机床加工精度的主要手段。
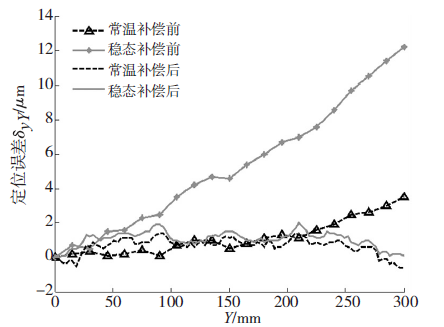
图6 Y 轴误差补偿效果
本次试验采用误差补偿法, 借助精密研抛数控机床误差补偿控制器模块, 依据式(7) 几何误差与热误差复合模型计算得到的机床冷态和稳态时的补偿量输入到机床误差补偿表中进行补偿实验,补偿结果如图6 所示,冷态时最大定位误差从3. 5μm 降低到1. 2μm,误差降低了65.7%,稳态时最大定位误差从12. 2μm 降到1. 9μm, 误差降低了84.4%,补偿效果十分显著。
4.结论
(1)本文依据精密研抛数控机床y 轴温升与其定位误差变化关系的基础上,提出了基于牛顿插值法与最小二乘法的几何与热复合误差建模方法,该误差模型计算量小,效率高,可以获得较高的预测精度。
(2)根据几何误差与热误差的复合模型对机床进行误差补偿实验,实验表明该模型可以在不同温度和工况条件下进行误差补偿,补偿效果显著,有效提高了机床的加工精度。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息




