机床无刷直流电机系统的分岔分析与控制*
2016-9-6 来源:东北电力大学理学院 作者:张中华 付景超 邓冠男
摘要:文章主要研究了机床无刷直流电机系统的Hopf 分岔控制问题. 首先,对系统进行分岔分析,通过计算极限环曲率系数判定系统的Hopf 分岔类型; 然后设计Washout 滤波器对系统进行分岔控制,根据Hopf 分岔理论给出使原系统Hopf 分岔位置发生改变的参数条件,利用Normal Form 方法计算出受控系统的Hopf 分岔正规型,根据正规型的实部大小判定Hopf 分岔类型,给出使原系统Hopf 分岔类型发生改变的参数条件; 并借助MATLAB 软件对理论结果进行数值仿真,理论结果和数值仿真表明: 控制器中的线性增益能使系统在所期望的参数值处发生Hopf 分岔,甚至消除Hopf 分岔,控制器中的非线性增益能改变原系统的Hopf 分岔类型及极限环幅值的大小. 研究结果对无刷直流电动机系统的工程实际具有一定的指导意义.
关键词:Hopf 分岔, 分岔控制, Washout 滤波器, 无刷直流电机
0、引言
无刷直流电动机系统是集永磁同步电机、位置检测元件和驱动控制电路于一体的机电一体化产品,它既具备交流电动机结构简单、运行可靠、维护方便等一系列优点,又具备直流电动机运行效率高、无励磁损耗等优点,在伺服和驱动系统中得到广泛应用. 但在实际运行当中,在一定的参数条件下,系统会出现分岔行为,进而导致混沌运动,表现为电流波形出现不规则的电流噪声,电机转速忽大忽小,随机波动,电机运行性能不稳定等. 这种混沌现象在机床,特别是在精密机床的传动系统中是不允许出现的,因此对直流电机系统分岔、混沌及其控制方面的研究一直备受关注. 但到目前为止,大部分文献主要集中研究非线性动力系统的分岔行为及混沌控制问题[1 - 2]. 文献[3]建立了无刷直流电机的等效无量纲模型,分析了模型解的稳定性情况. 文献[4]在此基础上进一步研究了无刷直流电机的Hopf 分岔行为和混沌现象,但没有进行这方面的控制. 文献[5 - 7]在文献[3 - 4]的基础上分别采用不同的方法对无刷直流电机的混沌现象进行控制,从而保证了电机运行性能的稳定性. 但对系统的分岔控制没有研究,分岔是导致混沌产生的一种途径,对系统进行分岔控制有时可避免混沌的产生,进而减少混沌对系统造成的危害. 文献[8 -10]利用这种方法对混沌系统进行了分岔控制.
基于上述原因,本文在文献[4]和文献[7]的基础上,对无刷直流电机系统的等效非线性数学模型进行研究,首先讨论系统的Hopf 分岔类型,然后设计washout 滤波器对系统的Hopf 分岔行为进行控制,进而控制混沌的产生,保证电机运行性能稳定性. 主要利用Hopf 分岔理论及Normal Form 直接方法,给出原系统Hopf 分岔点提前、延迟或消失应满足的参数条件和原系统Hopf 分岔类型发生改变应满足的参数条件,并借助MATLAB 软件对理论结果进行数值仿真,分别给出控制前、控制后的分岔图以及分岔周期解振幅( 极限环幅值) 随参数变化的曲线图. 通过理论及仿真结果说明控制器的有效性.
1、系统分岔分析
在转子磁场定向坐标系( d - q) 中,由电压平衡方程和转矩平衡方程可得无刷直流电机状态方程为[2]
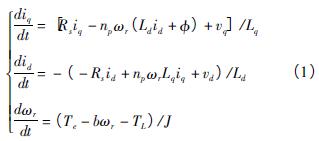

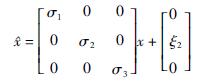
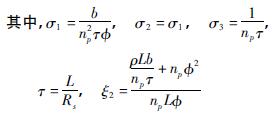









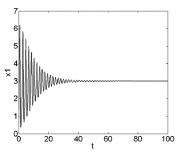
图1 σ = 4,ρ = 10,系统( 2) 波形图
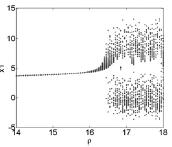
图2 σ = 4,ρ = 16 时,系统( 2) 分岔图
2、系统Hopf 分岔控制
取σ = 4,用washout 滤波器控制的等效无刷直流电机受控系统如下
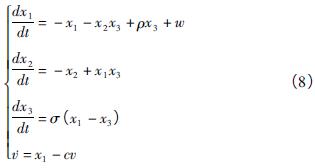
x1为washout 滤波器的输入变量,c 为滤波器时间常数,c > 0 时,为稳定的washout 滤波器,c < 0 时,为不稳定的washout 滤波器,现取控制器

2. 1 线性控制部分对Hopf 分岔的影响
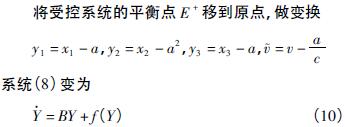
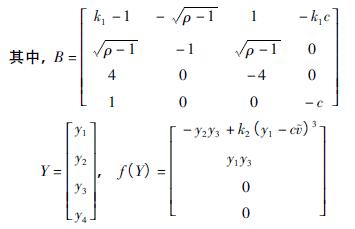


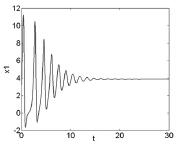
图3 k1 = - 1,ρ = 16 时,系统( 8) 波形图
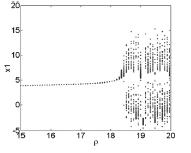
图4 k1 = - 0. 1,ρ = 18. 3368 时,系统( 8) 分岔图
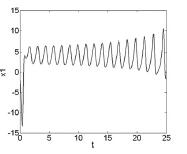
图5 k1 = - 0. 1,ρ = 18. 3368 时,系统( 8) 波形图
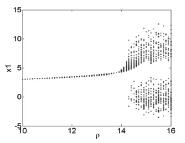
图6 k1 = 0. 1 时,ρ = 13. 9238 时,系统( 8) 分岔图


2. 2 非线性控制部分对Hopf 分岔的影响
当取c = 1,k1 = - 0. 1 时,ρ = 18. 3368. 方程( 10) 中的线性和非线性部分分别为
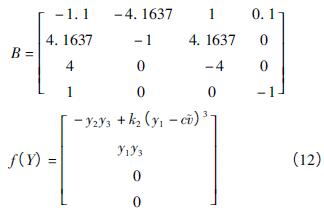




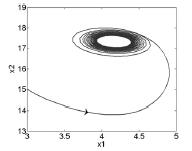
图7 当ρ = 18. 3368,k1 = -0. 1,k2 = -1. 5 时,系统⑻极限环
根据Hopf 分岔理论知,当Re( C) <0,即k2 < - 0. 347时,系统( 8) 在ρ =16 处发生超临界Hopf 分岔,即原系统Hopf 分岔类型被改变,不稳定极限环变为稳定极限环,如图7 -8 所示. 取k1 = -0. 1,将λ 看成分岔参数ρ 的函数,方程( 11) 两边同时对ρ 求导,得
计算得
α'( 0) = Re( λ'( ρ) ) | ρ = 18. 3368,λ = 4. 4768i =0. 0445 >0所以,当Re( C) <0 时,Hopf 分岔方向为ρ >16,如图9 所示; 受控系统的极限环幅控关系如图10 所示. 从图7,图8 及图10 中可知,控制器的非线性部分能改变原系统的Hopf 分岔类型,并且分岔极限环幅值随着非线性控制参数的增大而增大,成正比关系.
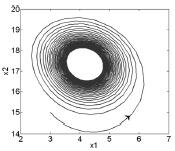
图8 当ρ = 18. 3368,k1 = -0. 1,k2 = -0. 1 时,系统⑻极限环
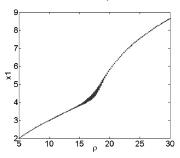
图9 k1 = -0. 1,k2 = -0. 06 时,系统⑻分岔图
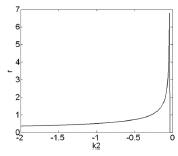
图10 系统⑻的限极环幅值曲线ρ = 18
3、结论
文章主要研究了机床无刷直流电机系统的Hopf 分岔控制问题. 首先,研究了系统的分岔行为并判定系统的Hopf 分岔类型; 然后设计Washout滤波器对系统进行分岔控制,讨论了控制参数对Hopf 分岔点位置,分岔类型以及极限环幅值的影响; 并借助MATLAB 软件对理论结果进行数值仿真,理论结果和数值仿真表明: 线性控制参数能使系统在所期望的参数值处发生Hopf 分岔,甚至消除Hopf 分岔,非线性控制参数能改变原系统的分岔类型,使不稳定极限环变为稳定极限环,并能改变极限环幅值大小. 研究结果对无刷直流电动机系统的工程实际具有一定的指导意义.
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com




