基于最优匹配区域的结构光系统的投影仪标定
2017-5-26 来源:湖北文理学院机械与汽车工程学院 作者:王中任 万仁全 刘亚俊
摘要:针对现有的投影仪标定算法精度不高的问题,根据投影仪的非线性模型,提出一种基于最优匹配区域的新投影仪标定算法。首先通过试验得到最优匹配区域,然后在最优匹配区域内计算角点的局部单应性矩阵,最后采用相机标定的方法对投影仪进行亚像素级标定。实验结果表明,该方法标定过程简便,投影仪标定误差最大为01 061 7 pixel,算法的执行时间为01 907 s,系统三维重构的点云密度达91 4 个/mm2。该方法只需要普通的平面标定板,操作简单,可满足高精度的三维测量系统要求。
关键词:结构光测量;三维重构;投影仪标定;局部单应性
1.引言
由于其非接触、自动化程度高、速度快、高精度等优点,结构光三维测量在产品设计与制造、质量检测中获得了广泛应用[1 -3]。在结构光三维测量系统中,投影仪标定技术是获得高精度的三维测量最基本和关键的环节[4],它主要包括投影仪的内参标定,以及投影仪和摄像机坐标系之间变换矩阵的确定。文献[5]标定精度较低,难以实现高精度的测量。文献[6]要求标定过程中移动投影仪,限制了其应用场合。文献[7]标定过程复杂,且不易实现。文献[8]成本昂贵,难以在实际工程中应用。文献[9]在计算单应性矩阵时耗时很长,造成整个标定程序效率不高,而且算法对结构光解码精度要求很高,对解码误差的鲁棒性不强,因此很难适应工业现场的高实时性和高可靠性要求。
本文在现有的算法基础上,提出一种基于最优匹配区域的结构光系统中投影仪标定算法,先用最优匹配区域计算每个角点的局部单应性矩阵,然后由投影仪的线性针孔模型和非线性畸变模型标定出投影仪的内参矩阵,最后用传统的双目标定方法得到投影仪-摄像机的外参矩阵。实验表明本方法适用于大视场、高精度的三维实时测量,很好地解决了上述方法在实时性和可靠性方面的不足,不仅操作简单易行,而且大大提高了系统的标定精度和系统鲁棒性。
2.标定原理和算法流程
2.1投影仪的理想针孔模型
按照前面所述,投影仪看作一个逆向的摄像机,所以投影仪模型可用与摄像机相同的理想针孔模型表示,基于单摄像机-单投影仪的结构光三维测量系统如图1 所示。
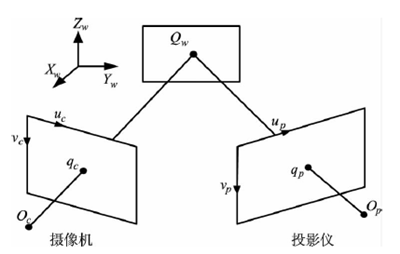
图1 结构光系统示意图

式中,参数s 为尺度系数;H 为单应性矩阵,表示为世界坐标系与投影仪像平面坐标之间的映射关系,由两部分组成:(1 )外参矩阵:即投影仪坐标系同世界坐标系之间的旋转矩阵R 和平移向量T,表示为

2.2投影仪的畸变模型
在设计、加工和组装光学镜片等过程中不可避免地会导致镜头非线性畸变,从而导致实际的成像点与理想成像点存在误差,这时在标定过程中需要引入畸变因子进行校正。这里主要考虑镜头的切向畸变和径向畸变[1 0],模型表示如下:

2.3标定方法
尽管投影仪在参数标定部分可以采用与摄像机完全一样的数学模型,但却无法直接得到平面棋盘标定板上每个角点的投影仪像平面下的像素坐标。因此,投影仪标定的首要难题是如何确定在投影仪投影平面上由像素点对应的空间三维坐标。如图2 所示,本文先把平面棋盘标定板以某姿态放置在空间世界坐标系中,将水平和竖直的格雷码条纹按不断细分的次序投射到标定板上,相机捕获到图片后,先利用由文献[1 1 ]的方法计算出的直接光分量和间接光分量来进行光条纹阈值分割,然后由格雷码解码算法得到投影仪像平面每个点的像素坐标。利用不同匹配区域,使得摄像机像平面与投影仪像平面之间的单应性矩阵泛函数取得最小值来获得最优化单应性矩阵,得到标定板每个角点的投影仪像平面下的像素坐标。
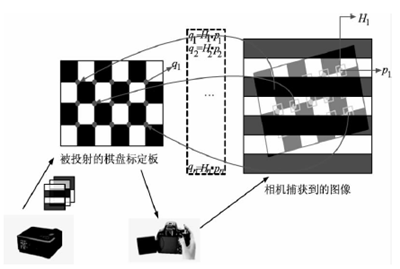
图2 结构光系统标定示意图
标定投影的具体流程如下:
(1 )平面棋盘标定板以某姿态放置在空间世界坐标系中,投影仪投射出42 幅格雷码结构光图案到平面棋盘标定板,投射的次序是1 幅全白、1 幅全黑、20 幅水平方向、20 幅竖直方向格雷码结构光图案,并且依次被相机所捕获。
(2)使用第一张标定板图像,提取棋盘标定板角点的亚像素级的坐标(xc,yc)。
(3)设S ={I1 ,I2,…,Ik}为输入的格雷码结构光条纹图像序列,p 为图形上的某个像素点,点p 的直接光分量和间接光分量分别为Ld(p)和Lg(p),则有:
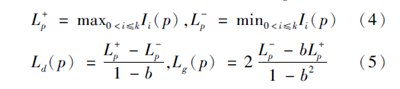
其中,b ∈ [0,1 ),是由投影仪投射的暗条纹灰度值决定的。利用图像每个像素点的Ld(p)和Lg(p),对图像中的格雷码条纹进行亚像素级阈值分割,然后用格雷编码的逆过程对阈值分割后的图像进行解码,得出每个投影仪图像上的每个像素点坐标。
(4)设点a 为相机图像上的某一个像素点,b 点为a 对应在投影仪图像平面上的像素点,a 和b 在各自像平面的齐次像素坐标为:

匹配区域H 过大,使得该式收敛速度很慢,算法效率低下;而匹配区域H 过小,又会对标定的精度有不利的影响。故本文通过实验定量地研究了匹配区域的大小同投影仪标定算法的精度和效率之间的关

这样,可以求出每个在相机图像坐标系下的角点亚像素坐标(xc,yc)对应在投影仪图像坐标系下的亚像素坐标(xp,yp)。
(5)在相机和投影仪的视野范围内,尽量较大程度改变标定板的空间姿态,重复以上步骤,得到至少3 组不同标定板姿态图片。由于本标定方法使用的是每个标定板角点坐标,而并非是整个棋盘标定板平面,因此适用于22 节非线性投影仪模型。最后利用张正友的相机标定方法来对投影仪的内外参数进行标定。
3.标定实验及结果分析
3.1标定实验
使用图3 所示的三维测量系统对本文所述的投影仪标定算法进行测试验证,该系统由一个DLP 投影仪(型号为BenQML6277,所选分辨率为1 024 ×768)和单反相机(型号为Cannon EOS650D,所选分辨率为51 84 ×3456 )组成;标定的软件环境为opencv -243 和VS201 0。标定过程中,按照上述步骤从6 个不同棋盘标定板姿态来采集图像,其中图4 为实验中三组标定板不同空间姿态下的水平和竖直格雷码解码结果,图5 为由对应姿态下投影仪反投影生成的虚拟图像。

图3 结构光测量系统

图4 水平和竖直格雷码解码结果


图5 投影仪反投影生成的虚拟图像
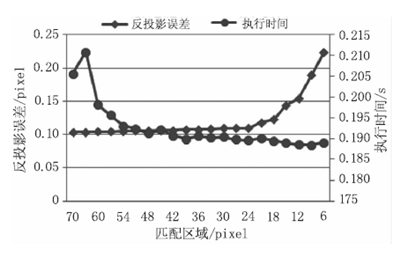
设定不同的匹配区域,用反投影误差来衡量投影仪的标定精度;用标定算子执行的时间来衡量投影仪的标定效率,反投影误差和执行时间结果如图6 所示。
3.2实验结果分析
由实验结果可知,匹配区域由70 pixel 降到24pixel 时,投影仪标定算子的反投影误差升高了0005584 pixel,最大反投影误差为01 09089 pixel(匹配区域为24 pixel 时),相比最小反投影误差01 03505 pixel (匹配区域为65 pixel 时)增大了5395%,因此可知,出在此区间内,匹配区域的增大并没有显著降低投影仪标定的精度。但是当匹配区域由24 pixel 降到6 pixel 时,投影仪标定算子的反投影误差升高了01 1 41 92 pixel,最大反投影误差为0223281 pixel(匹配区域为6 pixel 时),相比最小反投影误差01 09089 pixel(匹配区域为24 pixel 时)增大了1 04678%。由此分析可知,投影仪标定算法有个最优匹配区域的取值范围,若是小于该范围,会造成标定精度的大幅度降低。
在算子执行时间方面,匹配区域由70 pixel 降到42 pixel 时,投影仪标定算子的执行时间降低了00201 s,最长执行时间为021 08s(匹配区域为65pixel 时),相比最短执行时间01 907s(匹配区域为42 pixel 时)要长1 0540%;但是当匹配区域由42pixel 降到6 pixel 时,投影仪标定算子的执行时间只降低了00023 s,最长执行时间为01 907 s(匹配区域为42 pixel 时),相比最短执行时间01 884 s(匹配区域为9 pixel 时)要长1 221 %。由理论原理和实验结果分析可知,计算单应性矩阵时的匹配区域对投影仪标定的效率和精度有很大的影响,在本实验硬件条件下,匹配区域选择24pixel 至48 pixel 时,保证了标定的精度同时兼顾标定效率,是理想的匹配区域范围。因此,选取匹配区域为42 pixel 作为最佳匹配区域,反投影误差ep =01 061 7,标定得到的投影仪外参和内参如表1 所示,图7 为使用该标定结果来进行的三维重构实验结果。
表1 投影仪标定结果


图7 三维重构结果
4.结论
在由摄像机-投影仪组成的结构光三维测量系统中,相机的标定和投影仪的标定是获得高精度测量结果的关键。本文将投影仪当作一个逆向的相机,建立了投影仪模型,由于使用的是未标定的摄像机,故投影仪的标定精度不受摄像机标定误差的影响。标定算法中的投影仪像素与摄像机像素之间的匹配区域对标定的效率和精度有很大的影响,本文通过实验定量地研究了匹配区域与精度和效率之间的关系,并分析得出了在本实验硬件条件下的最佳匹配区域。实验表明,在最佳匹配区域下,投影仪的标定精度达到01 061 7 pixel,效率为01 907 s。在对三维测量系统进行摄像机和投影仪标定后,对一个尺寸为20 mm ×20 mm ×20 mm 的标准块进行三维重构,得到的三维点云密度为91 4 个/mm2,拟合可得标准块的边长为最终重构20072 mm,测量绝对精度为0072 mm。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com





