主轴集成式光纤光栅切削力测量方法研究
2017-3-3 来源:武汉理工大学机电工程学院 作者:刘明尧,陈功,张志建,邴俊俊
摘要:为了稳定可靠地测量切削加工过程中切削力的大小以对机床的加工状态进行监测(TCM),对基于光纤光栅(FBG)传感技术的主轴集成式切削力测量方法进行了研究。基于光纤光栅应变检测原理和Γ形梁的受力分析,提出了4 个完全相同并且对称的Γ形梁弹性体结构;通过对切削力传递规律的分析,建立起了主轴集成式切削力测量理论模型并确定FBG 的布点;为了验证模型的准确性,搭建了主轴集成式光纤光栅切削力测量实验平台,最后通过实验验证了该方法的可行性和可靠性。
关键词:光纤布拉格光栅;主轴集成;切削力;Γ形梁
1.引言
切削力是描述切削加工过程中最重要的特征,其大小和动态变化反映了切削过程中刀具与工件的相互作用情况和工件表面的形成过程。通过监测切削加工过程中切削力的变化可以间接反映刀具切削状态的变化,因此切削力的精确有效测量对于机床加工状态的监测(toolcondition monitoring,TCM)具有重要意义。Yaldiz S 等人[12]基于应变片设计了八角环结构的车削和铣削测力仪;Panzera T.H.等人[3]基于应变片设计出空心圆柱双端固定梁结构的车削测力仪;程金生等人[4]基于应变片设计了轮辐型车削力传感器;Rizal M等人[5]基于应变片设计了Γ形梁结构的切削力测力仪;而Song A 等人[6]基于Γ形梁结构设计了应变式多维力传感器;大连理工大学的张铁等人[7]设计出了压电式车削测力仪,瑞士的Kistler 公司是压电式测力传感器领域的全球引领者,研制出各种类型的测力装置,国外的许多学者如Totis G 等人[8]、Scippa A 等人[9]等都使用Kistler 公司的测力传感器在切削力测量领域做了大量研究;Jin W.L.等人[10]和Albrecht A 等人[11]利用位移传感器检测刀具或主轴的位移来反映切削力的大小,并搭建了铣削力测量系统。然而应变片粘贴工艺复杂,处理电路较多,容易受到电磁干扰;压电材料对环境温度湿度要求较高,价格比较昂贵且本身具有滞后特性;基于位移测量的检测系统采集的信号干扰因素多,不能直接反映刀具的工作状态。刘明尧等人[1213]提出基于光纤传感技术的八角环结构切削力测量方法;蒋奇等人[14]则提出了基于光纤传感技术的Γ形梁结构多维力测量方法,但其都是工作台式传感器,通过工作台这个媒介间接地测量切削力,工件的大小和质量会对切削力的测量产生影响。光纤光栅传感技术制作的传感器具有对电绝缘、抗电磁干扰能力强、适用于恶劣环境的测量、体积小、能够在单根光纤上实现分布式测量等优点。因此本文基于光纤光栅传感技术提出了集成在机床主轴上的切削力传感检测方法,设计了传感器结构,搭建了实验平台,验证了主轴集成式光纤光栅切削力测量方法的可行性和可靠性。
2.光纤光栅应变检测原理
光纤光栅反射波的波长同时受反向耦合模有效折射率以及光栅周期影响。它们之间的关系满足光栅方程[15]:
而温度和力都会使光纤光栅的反射波长发生变化,由于本文设计的传感器集成在主轴上,远离切削加工过程中的热源,因此认为温度不变,仅考虑切削力的影响。当光纤光栅受到力的作用而产生拉伸或压缩的时候,光栅周期会发生一定的变化,同时光纤本身的弹光效应会使有效折射率也产生变化。基于此,可以建立光纤光栅的应变传感模型如式(2)所示,它表示了当光纤光栅处于轴向应变作用状态下时,光栅的反射波长漂移量与轴向应变之间的关系。

出相应测点的应变大小。
3.转换弹性体设计
3.1 Γ形梁受力理论分析
基于前人对于Γ形梁结构测力传感器的研究,通过FBG 传感技术将其集成在主轴上测量切削力的大小,下面分析其受力时的应变分布特征。
主轴上的传感器在切削加工过程中5 个自由度受到限制,只有沿轴向转动的自由度,因此仅分析Γ形梁受FX2、FY2、FZ2、MX2 和MY2 作用时的应变分布特点,如图1 所示。

图1 Γ形梁受力示意图
根据材料力学可以分别求出各个分力作用时a、b、c3 点的应变值,将他们分别相加即可得到Γ形梁受力时各个点的总应变大小,如式(5)所示。

3.2转换弹性体的结构设计
对称结构受力均匀且便于切削力的解耦,因此本文基于Γ形梁的结构设计了4 个完全相同并且对称的Γ形梁弹性体结构,如图2 所示。它包括与主轴相连的中间轴部分、作为弹性元件的4 个Γ形梁和与刀具相连接的底部圆盘。

图2 转换弹性体结构
弹性元件的力学特性由其材料和结构决定,考虑到抗腐蚀性、环境因素、刚度等,本文选用304 钢作为弹性体的材料。
4.切削力传递规律和FBG 布点
4.1切削力传递规律
转换弹性体的结构简图如图3 所示,将其4 个Γ形梁分别记为Ⅰ、Ⅱ、Ⅲ、Ⅳ。

图3 转换弹性体各梁编号
先定义3 个直角坐标系:
1)固定坐标系XYZ:原点O 为铣刀的刀尖点,Z 向为主轴的轴向,X 和Y向为工作台的横向和纵向进给方向。
2)旋转坐标系X1 Y1 Z:原点O1 与O 点重合,X1 方向则为弹性体梁Ⅰ和梁Ⅲ所在方向,Y1 方向为弹性体梁Ⅱ和Ⅳ所在方向。
3)旋转坐标系X2 Y2 Z2 :原点O2 为转换弹性体底部圆盘上表面的中心,而X2 、Y2 和Z2 向分别与X1 、Y1 和Z平行。
由图4 中XYZ 与X1 Y1 Z 的相对位置可以得到2 个坐标系之间的关系如下:

图4 固定坐标系XYZ 与旋转坐标系X1 Y1 Z


图5 旋转坐标系X1 Y1 Z 与弹性体旋转坐标X2 Y2 Z2



图6 弹性体受Fx2 、My2 作用时变形示意图
图6 为弹性体受Fx2 和My2 作用时的变形示意图,其中实线表示变形前,虚线表示变形后的情况。由于梁Ⅰ相对于底部的圆盘有一个Z 方向的位移,为了抑制这一相对运动趋势,底部圆盘对梁Ⅰ还会产生一个Z 方向的力,记为FIZ0。同理,圆盘对梁Ⅲ也会产生一个Z 方向的力,它们大小相等,方向相反。故此时梁Ⅰ受到3 个力的作用分别为FIX、FIZ0 和MIY,结合变形的协调性,可以得到如下变形协调方程组:








4.2FBG 布点
由于光纤光栅测量切削力实际上也是感知由切削力在弹性体上产生的应变大小。而应变式力传感器在布置应变测点时有应力集中的原则,即将测点布置在应变最大的地方,由3.1 节中的分析可知,应变最大的地方都在梁的根部,但是若将光纤光栅粘贴在梁的根部会导致光纤光栅的输出端光纤产生极大的弯曲从而导致解调仪无法解调出信号。所以,本文布点的原则是在保证解调仪能够解调出足够强度信号的前提下,尽量将光纤光栅贴到距离梁根部近的地方,并且贴在各梁表面宽度的中间处,即中性层上。
具体的布点及光纤光栅编号如图7 所示。本次选用的3 根光纤光栅中心波长分别为1 555 nm、1 550 nm 和1 537 nm,分别记为FBG1、FBG2 和FBG3。其中FBG1 粘贴在横梁的上表面,FBG2 粘贴在横梁的侧面,FBG3 粘贴在纵梁的表面,分别对应2.1 节中的a、b、c 3 点。

图7 光纤光栅的布点及编号
5.实验研究
5.1 切削力测量实验平台
为了通过实验验证主轴集成式光纤光栅切削力传感器数学模型(即式(22))的正确性以及传感器的可靠性,本文设计了主轴集成式切削力传感器实验平台。此平台的主要组成部分如图8 所示。

图8 主轴集成式光纤光栅切削力测量实验平台概览
实际搭建完成的平台如图9 所示。

图9 测量实验平台实物图
5.2传感器的静态标定
为了分析传感器的可行性和检测方法的可靠性,首先需要对传感器进行静态标定,即φ=0°时传感器输入与输出之间的关系。
5.2.1X 方向切削力的静态标定
平台装配完成后,转动主轴将弹性体调到初始位置(φ=0°)。接着利用径向力加载装置先给弹性体施加上X 方向的切削力,以0.2 kN 为步长,直至加到2 kN 左右(即依次分别施加0.2 kN、0.4 kN、0.6 kN、0.8 kN、1.0 kN、1.2kN、1.4 kN、1.6 kN、1.8 kN 和2 kN 的力),加载和减载各做3 次。将实验测得的三个FBG 的波长数据转换为应变后进行拟合,结果如图10 ~12。
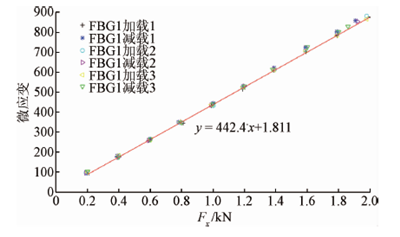
图10 X 方向力加减载时FBG1 数据拟合曲线

图11 X 方向力加减载时FBG2 数据拟合曲线

图12 X 方向力加减载时FBG3 数据拟合曲线
通过对比图10 ~12 可以很直观地看到FBG2 和FBG3 的拟合效果不如FBG1 好,误差较大,这是因为受X 方向切削力作用时,FBG2 和FBG3 处的应变水平与FBG1 处相比较低,特别是FBG2 处,满量程也才9 个微应变,而FBG1 处满量程有近900 个微应变。因此,X 方向的切削力主要由FBG1 来反映。由3 条拟合曲线可以得到当X 方向切削力作用时,各个FBG 产生的微应变大小规律,即式(25)所示。

5.2.2Y方向切削力的静态标定
完成X 方向的加减载实验后,接着进行Y 方向切削力的加减载实验。同理得到当Y 方向切削力作用时,各个FBG 产生的微应变大小规律,即式(26)所示。
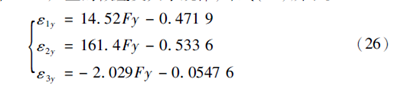
由式(26)可以看出当弹性体受Y 方向切削力作用时,FBG2 的应变水平最高,而FBG1 和FBG3 的应变较小,特别是FBG3 的应变大小相对于FBG2 来说基本可以忽略。因此,Y方向的切削力主要由FBG2 来反映。
5.2.3Z 方向切削力的静态标定
在完成X 和Y方向的加减载实验后,最后进行Z 方向切削力的标定实验,同理可以得到式(27)

可以看出当弹性体受Z 方向切削力作用时,3 个FBG 处的应变水平并没有如X 和Y 方向切削力作用时那么显著的区别,因此,Z 方向切削力测量的准确性也是最差的。
结合式(25)~(27)可以得到:

由于实际使用时需要根据测得的应变反求处切削力的大小,因此需要通过矩阵运算将式(28)的等号左边变为切削力矩阵,经过MATLAB 运算后,保留4 位有效数字,得到的结果如式(29)所示。

式(29)只是φ=0°时的切削力模型,还不是完整的数学模型,要想得到完整的切削力模型,还需要将转角矩阵代入其中。结合式(22)得到完整的切削力模型如式(30)所示。

5.3其他角度下传感器的静态实验
为了验证式(30)在φ≠0°时的适用性,还分别进行了φ=30°和φ=45°时的静态试验。首先以φ=30°为例,将初始状态下的转换弹性体转过30°,依次分别给X、Y、Z 方向加上1 000 N 的切削力,分别记下3 个状态下3 个FBG 的波长数据。将其转化为微应变后如表1 所示。
表1 φ=30°时FBG 微应变大小

将φ=30°,FX =0.99 kN 时各个FBG 微应变大小代入式(30)的模型中,算得FX =0.966 9 kN,误差为2.3%,同理可求得FY =1.044 kN,误差为3.4%,FZ =1.085 kN,误差为7.4%。
再将弹性体调到φ=45°的状态,同样的实验过程得到表2。
表2 φ=45°时FBG 微应变大小

此状态下算得FX =0.960 6 kN,误差为4.9%,FY =1.057 kN,误差为4.7%,FZ =0.932 0 kN,误差为7.7%。考虑到实验过程中标定时力传感器的误差、角度测量的误差、光纤光栅粘贴的位置和质量好坏以及室温的波动等影响,根据上述实验结果和误差可以认为主轴集成式光纤光栅的切削力测量方法在静态时是可行的,式(30)的理论模型在静态时是可靠的。
5.4动态实验
验证了静态时切削力模型的正确性,为了验证其在动态时也是适用的,本文还在实验平台上完成了主轴集成式光纤光栅切削力传感器的动态实验。由于还未安装角度传感器,为了验证切削力模型在动态时的正确性,本文将不同主轴转速、不同切削力作用下FBG 的波长数据进行对比,验证其是否满足切削力模型。
5.3.1径向力动态实验
首先将式(30)做变换,将FY =0、FZ =0 代入式中得到3 个FBG 应变大小与FX 和主轴转角之间的关系如式(31)所示。

由式(33)可以看出,当主轴匀速转动且切削分力FX单独作用时,3 个FBG 的应变(或波长)大小随着时间呈正弦函数变化,且其幅值大小与转速无关,而与力FX 的大小成正比,转速n 则影响正弦函数的周期。
1)相同转速,不同径向力
首先将主轴转速调到200 r/min,并且给弹性体加上1 000 N 的X 方向切削力,得到3 个FBG 波长数据随时间变化的关系如图13 所示:

图13 n =200 r/min,FX =1 kN 时3 个FBG波长随时间变化
由图13 可以看出,3 个FBG 的波长数据均呈正弦函数变化,且周期相同。保持转速不变进行FX =500 N、1 500 N 的实验,将3次实验FBG1 的数据作对比,如图14 所示。

图14 n =200 r/min,FX =0.5 kN、1 kN、1.5 kN时FBG1 的波长
由图14 可以看出,相同转速,不同FX 作用下FBG1的波长均呈正弦函数变化,且周期相同,但幅值不同,FX =1 kN 时的幅值为FX =0.5 kN 时的2 倍,而FX =1.5 kN时的幅值为FX =0.5 kN 时的3 倍,FBG2 和FBG3的规律和FBG1 相同,由此可知FBG 的应变大小和FX 成正比,满足式(33)。2)不同转速,相同径向力将FX 设定为1 kN,再分别进行n =100 r/min 和n =300 r/min 的实验,测得的FBG1 的波长数据如图15 所示。

图15 FX =1 kN,n =100 r/min、200 r/min、300 r/min时FBG1 的波长
由图15 可以看出,不同转速,相同FX 作用下FBG1的波长同样呈正弦函数变化,但与相同转速不同FX 情况下不同的是,FBG 在不同转速条件下的幅值基本相同,而周期不同,其中n =200 r/min 时的周期为n =100 r/min时的1 /2,n =300 r/min 时的周期为n =100r/min 时的1/3,FBG2 和FBG3 的规律也和FBG1 相同,即周期大小与力无关,而与转速成反比。显然,这也满足式(33)的规律。
由上述分析可知,径向力的动态实验中,FBG 的应变规律满足切削力模型。由于FX 和FY 都是径向力,它们的规律完全相同,因此可以认为在不同径向力作用下的动态实验中,FBG 的应变规律满足切削力模型。
5.4.2轴向力动态实验
将FX =0、FY =0 代入式(30)中得到3 个FBG 应变大小与FZ 之间的关系如式(34)所示。

由式(34)可以看出,当切削分力FZ 单独作用时,3个FBG 的应变(或波长)大小与转速和时间无关,只与FZ 大小成正比,下面通过实验验证其是否正确。将主轴n 转速设置为200 r/min,力FZ 设置为1 kN,得到3 个FBG 波长随时间变化的曲线如图16 所示。

图16 n =200 r/min,FZ =1 kN 时3 个FBG 波长
从图16 可以看出,3 个FBG 的波长并不是完全没有变化的,而是呈现一定周期性,似乎不符合切削力模型。然而这是由于动态实验中有干扰的原因,特别是动态切削过程中主轴的轴向跳动使得轴向加载套筒与力加载器之间的接触压力发生变化从而使加上的力FZ并不是恒定不变的,通过观察力传感器的读数,FZ 的变化范围约为0.2 kN,以FBG1 为例,其可以引起FBG1产生16.5 με的波动;再就是由于卧式安装,装置自身重力会对结果造成干扰,将简化模型导入ANSYSWorkbench 中进行仿真,可以得到由于自重在FBG1 上引起的误差在10 με以上,且这2 个误差都是随着主轴转动呈周期性变化的,也就是说各项误差源产生的实验总误差在26.5 με以上。而图16 中FBG1 的最大波长与最小波长之间的差值为40 pm 左右,对应微应变大小为33.2 με,然后由式(34)可知由1 kN 的FZ 在FBG1 处引起的应变大约为82.4 με,大于33.2 με,由此可见,图16 中的波长不是直线的原因并不是切削力模型错误,而是由于实验过程中的上述误差的存在而导致的,FBG2 和FBG3 也是如此。因此,去除这些误差因素后,可以认为在轴向力动态实验中,FBG 的应变规律基本满足切削力模型。根据径向力动态实验和轴向力动态实验可以认为切削力模型在动态时也是适用的。
6.结论
以切削力为研究对象,针对传统应变式和压电式测力传感器易受电磁干扰和平台类传感器易受工件质量和大小影响等问题,基于光纤传感技术提出了集成在主轴中的光纤光栅传感器。从理论上分析了切削力的传递规律和受切削力作用时弹性体的应变分布规律,建立了切削力测量的理论模型。并搭建了主轴集成式切削力传感器实验平台以进行实验分析。通过对理论分析和静、动态实验分析的对比,验证了该检测方法的可行性和可靠性。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息





