考虑机床结合面的立式加工中心动态特性分析
2021-2-2 来源:1.五邑大学;2.深圳创世纪机械有限公司 作者:吕超超,王瑞超,周俊荣,段周波
摘 要:以某企业的T-V855立式加工中心为研究对象,用虚拟介质法计算出机床结合面的动力学参数,建立整机有限元模型,进行模态分析,获得前6阶固有频率与振型。进行了T-V855立式加工中心实验模态测试,由实验结果与模型仿真结果对比可知,实验模态测试结果和整机有限元仿真的结果一致,最大误差为8.7%,验证了考虑机床结合面的整机有限元模型的合理性和正确性,同时对机床进行了谐响应分析,确定机床的关键部件为主轴箱与立柱,为后续机床二次设计提供了理论基础与方向。
关键词:结合面;接触理论;动态特性;模态测试
0、引言
T-V855立式加工中心具有高速、高效率等优点,主要对5G产品的零部件、LED框架等进行粗精加工。该机床的设计难点在于机床对工件的加工精度,而影响机床加工质量的主要因素就是机床的动态特性。因此,本文对机床的动态性能展开研究,首先使用虚拟介质法,假想一层虚拟材料来代替机床结合面,通过计算得到材料的弹性模量、泊松比等动态参数,进而建立机床整机的有限元模型;对机床进行模态分析,结合机床实验模态测试的结果,验证考虑结合面的机床模型的准确性;对机床模型使用谐响应分析以确定机床的关键部件,为后续机床二次设计提供了理论基础与方向。
1、结合面虚拟材料的解析模型
结合面的动态特性与机床部件的不同,结合面动态特性复杂,它的动态特性是非线性的,通过传统方法获得的结合面参数直接应用于工程难度很大。因此本文将采用虚拟介质法来获得机床结合面的动力学参数。虚拟介质法的原理是在机床零部件接合处假想有一层很薄的材料,通过假想的这层材料代替结合面,然后利用接触理论求解出虚拟介质的弹性模量、泊松比、密度等属性,通过这些参数代替结合面的属性,这样就可以间接地将结合面参数应用到工程中。
虚拟介质层的数字模型如下:
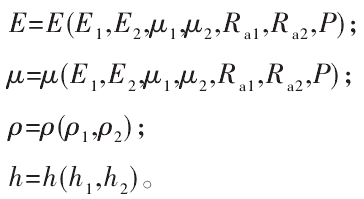
式中:E1、E2为结合面1和2的弹性模量;μ1、μ2为结合面1和2的泊松比;Ra1、Ra2为结合面1和2的微接触点半径;P为结合面所受的垂直载荷;ρ1、ρ2分别为材料1和2的密度;h1、h2分别为结合面材料1和2的微凸层厚度。
1.1、结合面虚拟介质的厚度h和密度ρ
T-V855立式加工中心的表面粗糙度为Ra0.8 μm,接触表面的微接触层厚度h1=h2≈0.5 mm,虚拟介质层的厚度是接触表面的微接触层厚度之和,所以虚拟介质层的厚度h取1 mm。虚拟介质由接触表面的微接触点组成,其平均密度计算公式为:
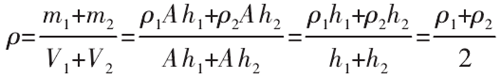
1.2、结合面虚拟材料的弹性模量E
结合面为接触表面上的微小接触点的结合,接触点能近似看作球体,因此,结合面可以近似看作由无数球体组成的。选择任意一个接触点进行分析,设两球体半径分别为RP1、RP2,接触点在载荷P的压迫下,球心距离缩小,产生局部干涉量w,如图1所示。使用赫兹公式得:
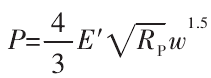
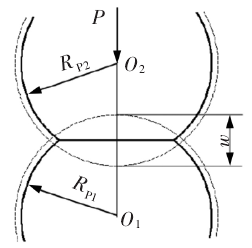
图1:微接触点接触示意图
同时:
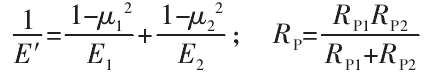
式中:E′为结合面的等效弹性模量;RP为等效半径。
由W-M函数可知两接触点产生的干涉量为:
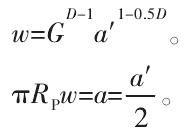
式中:G是分型粗糙度;D是表面轮廓分形维数;a′是接触点平截面积。
由式(3)、式(6)可得一个接触点的实际接触应力计算公式为:
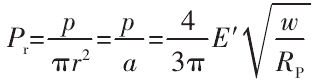
一个微接触点的正应变为:
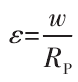
将式(8)代入式(7)得到一个接触点的正应力-正应变关系:
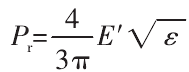
对式(9)求导得两接触点间的弹性模量为:
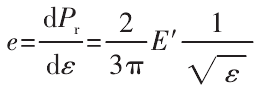
由式(5)、式(6)和式(10)得:
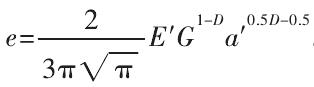
最大接触点的平截面积为:
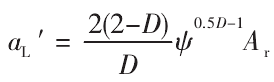
临界平截面积为:

式(12)、式(13)中:ψ为域拓展系数,与表面轮廓分形维数D值有关;Ar为真实接触面积;K=H/σy为相关系数;H为较软材料硬度;σy为较软材料屈服强度;φ=σy/E′为材料属性。
对结合面的所有接触求和,得到虚拟材料的弹性模量:
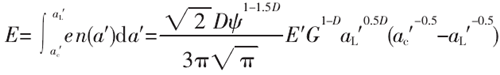
1.3、结合面虚拟材料的泊松比μ
在机床加工中,由于机床的自重,结合面会受到法向载荷P作用;由于机床主轴旋转,结合面同时受到切向载荷Qr作用,如图2所示。结合面在切向载荷Qr的作用下,接触面表面一部分产生相对运动,称为微滑区,剩余部分发生变形,称为黏附区。如图中所示,c为黏附圆的半径。c也称为微滑圆环的内半径;r为微滑圆环的外半径。这两个区域构成了接触点的整个接触表面。
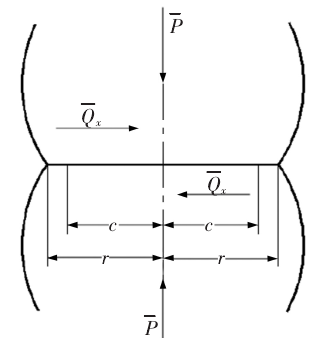
图2:微接触点所受载荷示意图
在黏附区中产生的切变位移为:
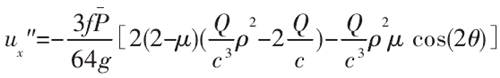
式中:Q为微滑区的待定常数;f为接触表面的动摩擦因数,它的取值由材料种类和接触面的物理条件决定;g为微接触点的切变模量。
在微滑区中,产生的切变位移为:
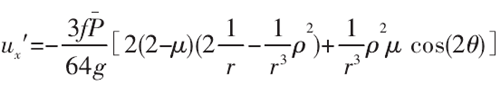
结合式(15)、式(16),得到总位移为:
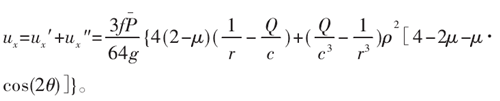
由于ρ、θ是常数,要使上式在任何情况下都成立,则:
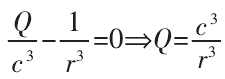
结合式(17)、式(18)得总位移:
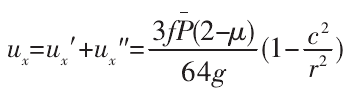
一个微接触点的微滑切向载荷计算公式为:
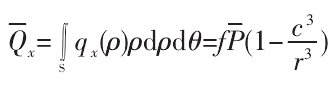
将式(20)代入式(19)得:
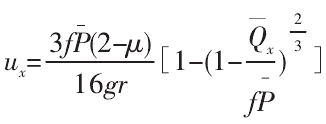
所以两微接触点的相对切向位移为:
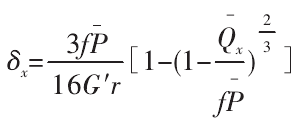
式中,G′为结合面的等效切变模量:
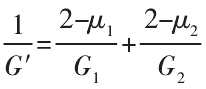
根据式(22),则两微接触点的相对切应变为:
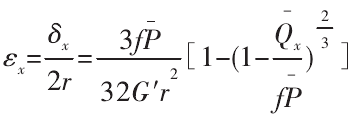
在实际的机床装配中,由于结合面表面粗糙,存在实际接触面积,实际接触面积与结合面所受载荷近似成正比:
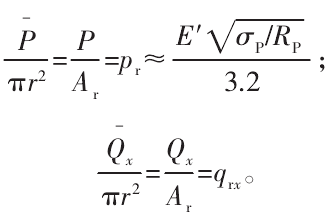
式中:σp为表面粗糙度标准差;qrx为黏附结点的实际剪切强度。
将式(26)除以式(25)得:
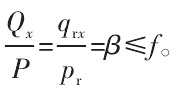
结合式(25)、式(23)得切应力-切应变关系:
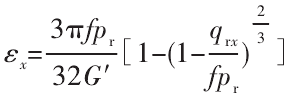
对式(28)求导得到两微接触点间的切变模量为:
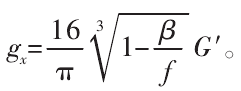
对接触中的全部微接触点求和,可得到虚拟材料的切变模量:

虚拟材料的等效泊松比为:
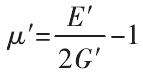
得虚拟材料的泊松比为:
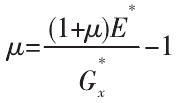
式中,E*、G*x分别为无量纲的虚拟介质弹性模量、切变模量:
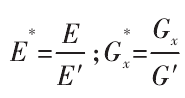
1.4、虚拟介质参数计算
T-V855立式加工中心的结合面基本分为机床床身与立柱的结合面及机床中所有导轨与滑块的结合面,对结合面使用虚拟介质法求取结合面参数。立柱与床身的材料均为HT250灰铸铁,材料密度为ρ1=ρ2=7340kg/m3,弹性模量为E1=E2=116 GPa,泊松比μ1=μ2=0.27,屈服强度为σy1=σy2=240 MPa,布氏硬度为H=700 MPa,表面粗糙度为Ra0.8 μm。
由式(2)得结合面的虚拟介质密度为ρ=(ρ1+ρ2)/2=7340kg/m3。
立柱-床身的名义接触面积Aa=68154 mm2,实际接触面积与名义接触面积的比例为Ar/Aa=[1-wsh(u)]/ 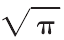 =0.034。
=0.034。
取表面轮廓分形维数D=1.1, 由表面轮廓分形维数计算得分形粗糙度G=3.68×107mm。
由表面轮廓分形维数得到域拓展系数ψ=2.4435。
利用式(12)、式(13),求解式(14)、式(30)、式(32)中各参数,得到机床床身-立柱结合面虚拟材料的动力学参数为:E=11.32 GPa,μ=0.28。
同理,得到机床导轨-滑块的结合面虚拟材料的参数为:E=13.56 GPa,μ=0.15。
其有限元模型如图3和图4所示。

图3:床身-立柱结合面模型示意图

图4:导轨-滑块结合面模型示意图
2、整机模态分析
2.1、整机有限元模态仿真
使用 SolidWorks 中的Simulation模块进行仿真分析。先将新建的结合面3维模型与整机进行装配,设置零部件的材料属性,使用通过虚拟介质法求得的结合面参数来设置结合面的材料属性,对模型施加固定约束,划分网格。建立整机的有限元模型,如图5所示。

图5:整机有限元模型
在机床实际加工中,结构的低阶固有频率更容易产生共振,因此本文主要仿真分析了T-V855立式加工中心的前6 阶固有频率。分析结果如表1 所示,机床振型如图6 所示。

图6:T-V855立式加工中心前6阶振型图
表1:T-V855 立式加工中心的前6 阶固有频率与振型描述

2.2、整机实验模态测试
对机床整机进行实验模态测试,对比机床仿真分析结果是否正确,修正仿真模型。采用INV306U频谱分析仪、INVYJ9A5096加速度传感器、YFF1-23力锤对机床进行力锤实验,收集实验数据,如图7所示。

图7:实验模态测试
使用DASP2006软件对采集到的信号进行分析,选择实验结果的前6阶固有频率与仿真分析结果进行对比,如表2所示。
表2:实验测得的前6阶固有频率与仿真结果对比
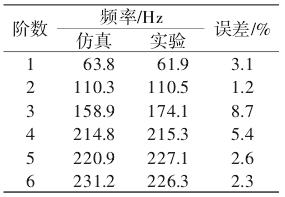
通过表2可知,利用仿真设计得到的前6阶固有频率与实验结果之间的最大误差在10%以内,说明建立的整机有限元模型是正确的,可以作为后续其他分析的基础模型。
3、谐响应分析
机床在工作过程中,由于机床主轴自转,会给予机床自身结构持续稳定的周期载荷,而谐响应分析就是分析机床自身结构在周期载荷激励下的响应情况。根据机床的工作情况,把幅值为1 N、频率为0~250 Hz的简谐力分别施加在主轴的3个坐标方向上,根据整机的响应情况,得到机床的频响曲线,结果如图8所示。
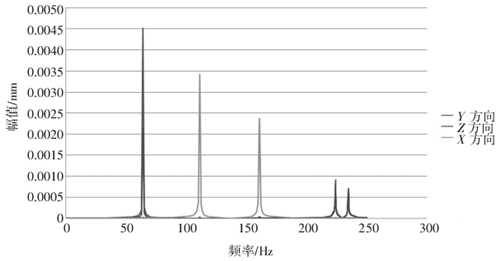
图8:T-V855立式加工中心频率响应曲线
从图8中可以看出,Z方向和Y方向的最大振幅出现在63 Hz附近,且幅值分别为4.5 μm和2.3 μm,对机床精度影响巨大,同时X方向对机床精度影响较大的振幅分别出现在110 Hz与160 Hz附近,幅值分别为3.4 μm和2.4 μm。以上振幅正好对应于整机的前3阶固有频率,参照整机的模态分析数据,可知机床的关键部件为主轴箱与立柱,所以在以后的设计中提高主轴箱与立柱的动态性能是提高机床性能的关键。
4、结论
实验模态测试的数据与考虑结合面的整机模态分析获得的数据基本吻合,说明通过虚拟介质法得到的结合面参数是可靠的;进而建立考虑结合面的整机有限元模型进行仿真分析是合理可行的;通过对整机进行谐响应分析可知,主轴箱与立柱为机床的关键部件,提高两者的动态性能是提高机床动态性能的关键。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息





