摘要: 针对某大型龙门加工中心的横梁进行多参数轻量化设计。对横梁结构进行有限元分析得出其初始的受力及变形情况。在保证横梁结构不变的情况下，以横梁的最大变形为约束条件，选择横梁的筋板厚度、出砂孔孔径等7 个结构参数作为设计变量，运用实验设计法对横梁进行轻量化设计。得到在横梁结构不变的条件下，7参数联合优化设计的设计变量参考值以及横梁总质量的响应变化值，优化设计的最优结果为横梁变形增加1． 81%的同时质量减轻2． 97%。

 
      0 引言

      横梁是数控机床的主要支撑部件，传统数控机床的横梁设计采用类比的经验设计方法，而且在验算横梁结构的强度与刚度时，常选择过大的安全系数，造成所设计横梁的结构尺寸与重量偏大，所以需要采用轻量化设计方法对其进行优化设计。

      优化设计作为机械设计中一种重要的科学设计方法，使得在解决复杂设计问题时，能从众多的设计方案中寻找到尽可能完美的或最适宜的设计方案 。轻量化设计是优化设计的一种，目的是通过对构件进行设计，使构件在满足使用要求的情况下重量尽可能地轻 。赵韩等人 利用参数化有限元法对液压机机身进行了轻量化设计; 吕国坤等人 基于遗传算法和响应面法对驱动桥桥壳进行了轻量化设计; 谭志洪等人 在天花板结构优化设计中采用了多方案优化设计，使得天花板钢耗降幅高达30% ; 王树英等人 对燃料电池轿车的前副车车架进行了轻量化设计，以模态特性为约束条件，使得车架自身质量得到大幅度降低; 万长东 对汽车发动机罩壳进行了多工况下的结构优化分析，使得汽车发动机在罩壳性能提升的同时，结构质量得到减轻。可见，通过轻量化设计方法，不仅可以减轻结构质量，而且可以解决传统方法所不能解决的比较复杂的优化设计问题。

      鉴于此，笔者希望通过轻量化设计方法对横梁结构进行多参数轻量化协同设计。首先，采用有限元分析技术获得横梁结构的应力场和变形场分布情况; 然后，根据优化要求建立优化模型，确定优化目标、设计变量、状态变量和约束函数，结合优化算法获得计算结果; 最后，在确保横梁结构满足使用强度的基础上，达到减少材料用量的目的。

      横梁结构轻量化方法的实施流程如图1 所示。首先，对一个新工程或新产品的功能进行分析，明确其具体要求、工作环境及外界条件，从而提出相应的解决方案; 其次，根据工程要求，简化实际模型，将对轻量化目标影响较大的参数确定为设计变量，利用CAD软件建立横梁的参数化模型; 再次，将各方案所得参数化模型导入Ansys 软件的Design Modeler 模块( 用于实现Ansys 和外部CAD 的交互) ，分别进行仿真计算，通过Simulations 模块得出横梁的应力、应变等云图，并初步比较这些方案的分析结果; 然后利用Ansys软件中的Design Xplorer 模块对各方案进行优化分析，通过实验设计( DOE) 法实现方案优化设计; 最后，综合考虑生产、工艺、运输和安装等多方面因素，在多个方案中进行优化比较且在多个目标之间相互协调，从中找出最佳方案，确定横梁的最优结构形式。

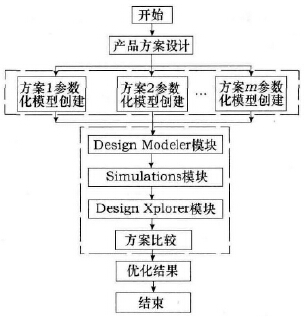
                   图1 横梁结构轻量化方法的实施流程
 

      1、 原横梁结构分析

      本文是在参考文献［9］的基础上对横梁进行的多参数轻量化分析，所以此处的原横梁结构分析直接引用参考文献 的分析结果。笔者在参考文献 中针对某大型龙门加工中心的横梁在实际工况下的应力及变形进行了分析，横梁三维装配体模型简图如图2 所示，横梁的质量为14 729kg。根据参考文献［9］的分析结果可知: 当滑鞍在横梁中间位置、滑枕伸出长度为全长的60%、机床主轴最大切削扭矩为5 010N·m时，横梁的变形量最大，将此工况下的横梁模型作为优化分析的基础模型，原横梁模型的变形仿真结果、原横梁装配体模型的应力仿真结果分别如图3 和图4 所示。

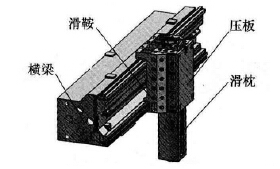
      图2 横梁三维装配体模型简图

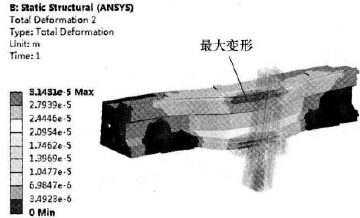
      图3 原横梁模型的变形仿真结果

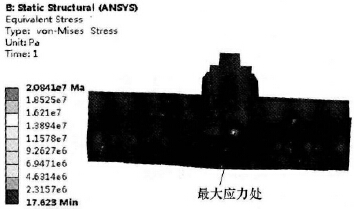
      图4 原横梁装配体模型的应力仿真结果

      2 、横梁轻量化设计模型建立
 
 
      在进行横梁结构的优化分析过程中，结构轻量化是主要目标，主要约束条件为横梁的变形，在满足给定的刚度、强度的约束条件下使横梁的质量达到最小。
 
 
      2． 1 目标函数
 
 
     通过优化结构的体积来达到减轻结构质量的目的，以质量最轻作为目标函数，即:

      2． 2 设计变量
 
 
     根据设计要求，考虑到横梁结构组成较复杂、尺寸变量较多，太多的设计变量增大了收敛到局部最小而非全局最小的概率，所以应尽量减少设计变量数量。采用变量关联的方法，以横梁结构上相互关联的尺寸建立传递方程式，即设计变量x 为:

      通过分析横梁结构可知，横梁主要由外部壳体和内部筋板组成，由于横梁外部壳体的结构与尺寸不可变动，故选取横梁内部筋板厚度，上、下出砂孔孔径等7 个参数即n = 7，进行多参数联合优化。7 个优化参数示意如图5 所示，对7 个优化参数的取值情况描述如下。

      1) 交叉筋板厚度t1( 见图5a) ，t1的优化初始值为25mm，其优化取值范围为22． 5 ～ 27． 5mm。

      2) 竖直筋板厚度t2( 见图5b) ，t2的优化初始值为20mm，其优化取值范围为18 ～ 22mm。

      3) 内部交叉筋板上的出沙孔孔径t3，t3的优化初始值为200mm，其优化取值范围为180 ～ 220mm。

      4) 横梁后部的上出沙孔孔径t4( 见图5c) ，t4的优化初始值为200mm，其优化取值范围为180 ～ 220mm。

      5) 横梁后部的下出沙孔孔径t5( 见图5c) ，t5的优化初始值为200mm，其优化取值范围为180 ～ 220mm。

      6) 横梁侧面出沙孔孔径t6( 见图5c) ，t6的优化初始值为180mm，其优化取值范围为162 ～ 198mm。

      7) 横梁底部出沙孔孔径t7( 见图5c) ，t7的优化初始值为200mm，其优化取值范围为180 ～ 220mm。

      
  
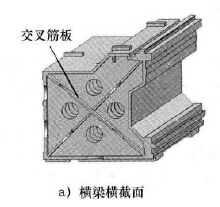
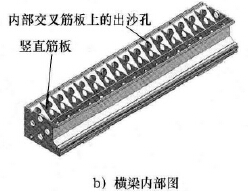
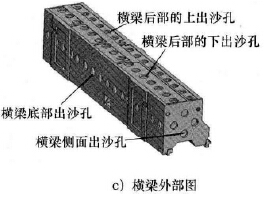
                                                      图5     7 个优化参数示意

      最终得到的横梁结构优化设计的数学模型为:

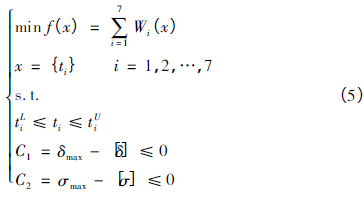
     式中: tUi、tLi分别为ti的上限和下限。运用Ansys 软件提供的基于实验设计( DOE) 方法［9］，根据输入参数的数目，利用目标驱动优化( GoalDrive Optimization，GDO) 技术，采集设计参数样点，计算每个样点的响应结果，利用二次插值函数构造设计空间的响应面或设计曲线，最终获得优化的解集。本文提出的横梁轻量化设计，就是在优化求解的实施过程中保持横梁结构不变，进行基于DOE 技术的多参数协同优化，获得横梁轻量化设计的最优结果。
 
 
      2． 4 横梁轻量化分析结果
 
 
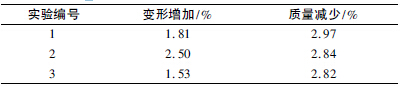
     根据本文建立的横梁轻量化设计模型，设置约束条件( 优化后变形增加量不超过5%，最大应力不超过最大应力限值) 并输出结果，通过软件仿真可计算出3组优化结果以供选择，如表1 所示，其中第1 组实验各构件的尺寸参数取值分别为: t1 = 22． 642mm，t2 =19． 073mm，t3 = 195． 56mm，t4 = 196． 74mm，t5 = 213． 79mm，t6 = 190． 74mm，t7 = 197． 24mm，此时的横梁最大变形量为3． 2 × 10 － 5m，比优化前增加了1．81%，横梁质量为14 291kg，比优化前减少了2． 97%，质量减轻效果相对最优。为了观察各个设计变量对分析结果的影响程度，利用Ansys 软件后处理模块进行灵敏度分析，得到各构件尺寸参数对输出结果的影响程度如图6 所示，从图6 所示可以看出，横梁内部交叉筋板厚度t1与竖直筋板厚度t2对横梁变形及横梁质量的影响程度远大于其他5 个因素，其他5 个因素对于横梁变形的影响程度由大到小依次为: t6 ＞ t4 ＞ t5 ＞ t7 ＞ t3; 对于质量的影响程度由大到小依次为: t6 ＞ t4 ＞ t3 ＞ t5 ＞t7，因此，在下一步的横梁结构设计研究中可着重考虑t1和t2两个影响因素。优化后横梁变形及质量的变化情况如表2 所示。

                                                                 表1 优化结果

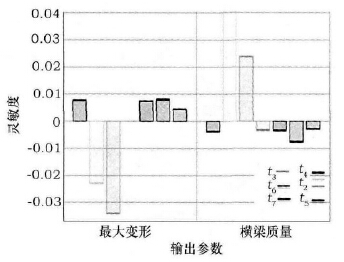
                          图6 构件尺寸参数对输出结果的影响程度

                             表2 优化后横梁变形及质量的变化情况

      3 、结语

     本文对某大型龙门加工中心横梁进行了包含横梁的筋板厚度、出砂孔孔径等7 个构件尺寸参数在内的多参数轻量化设计，得到在横梁基本结构不变的前提下，横梁变形增加1． 81%的同时质量减少2． 97%的优化结果。

     今后将重点研究横梁所有组成构件的结构尺寸参数对输出结果的影响，并找出影响最显著的参数，为进一步的横梁结构优化乃至变结构轻量化设计提供有益的参考。