【技术浅析】数控机床轴承结构振动谐响应及疲劳寿命研究
2020-11-9 来源:贵州师范大学 机械与电气工程学院等 作者:沈明明,李荣,刘祖国,汤耿
摘要: 以数控机床用的深沟球轴承为研究对象,分析其运转中的振型及结构疲劳寿命。首先通过Solidworks 建立了深沟球轴承的三维模型,利用ANSYS 对轴承进行模态及谐响应分析,获得轴承在固有振动频率以及在各阶次频率下的固有振型变化,同时借助有限元谐响应分析,确定了对轴承影响最大的模态频率。其次利用 ANSYS 中的 Faigue 模块对轴承进行了疲劳寿命研究,通过结合材料的 S-N 曲线理论以及 Hertz 接触理论,对轴承的疲劳寿命进行了预估分析。仿真结果表明: 在满足轴承强度工况下,固有频率 1125Hz 为结构共振最大点,且轴承的寿命范围为5937. 7 ~ 1 × 106次,为后续轴承结构优化提供参考。
关键词: 深沟球轴承; 模态振型; 振动谐响应; 疲劳敏感性; 疲劳寿命
0、引言
随着制造工业技术的快速发展,数控机床被广泛应用于关键零部件的加工制造,而主轴系统中轴承结构则是其运转的关键部件。轴承作为重大机械传动中的重要支承传动部件并且能够减少摩擦,因此轴承的好坏直接关系到机床加工精度和工作效率等性能。
同时轴承的振动疲劳破坏一直是影响机械结构运行的关键因素。近几年,国内外学者对轴承结构的运行状态及振动变化进行了研究分析,文献通过利用有限元法对航空圆柱滚子轴承的温度场及应力分布进行仿真分析同时还对轴承热力耦合下的疲劳寿命进行研究,文献通过建立接触模型,提出了一种载荷计算分布模型对深沟球轴承内部载荷序列与寿命进行计算。文献中HOUPERT 分析了滚动轴承在运行过程中对疲劳寿命造成影响的因素,上述研究都取得了一定的效果,但都只是单一的针对轴承的温度场及载荷序列进行研究。针对轴承振动谐响应与寿命的研究的报道并不多。
因此,本文以数控机床用深沟球轴承为研究对象,通过对轴承结构进行参数化建模,分析轴承静应力及模态振型变化。结合谐响应分析模块,利用模态叠加法分析深沟球轴内圈的谐响应变化。同时利用材料的S-N 曲线及疲劳灵敏度曲线对轴承进行了恒定载荷工况下的疲劳寿命研究,为数控机床主轴系统轴承振动疲劳分析及优化提供了参考。
1、深沟球轴承有限元分析
1.1、深沟球轴承静应力分析
轴承结构在运行过程中其结构的振型变化将会直接对结构的性能造成一定的影响,因此结构的振动特性决定了结构在不同载荷情况下的响应变化,所以对结构进行模态振型仿真分析具有重要意义。
由于在 ANSYS 中的建模工具并不成熟,因此本文利用 Solidworks 建立了深沟球轴承的参数化三维模型,通过转变模型的格式联立到 ANSYS 中进行分析,在进行分析时需要对结构的材料进行定义,本文分析时主要是利用有限元的方法进行利用,因此本文设定结构的材料都为轴承钢,其泊松比 为 0.3,密度为7810kg/m3,弹性模量为210GPa,设定完材料参数后,需要对结构的网格进行定义,因为在仿真分析时结构的网格是否合格直接影响到结构的分析精度,虽然系统有手动划分网格的功能,针对复杂的几何结构大多采用自动划分功能,通过设定网格为 Fine 划分得到如图 1 所示的深沟球轴承有限元网格模型,其中网格节点为10536,单元数为3950,网格质量为良好。
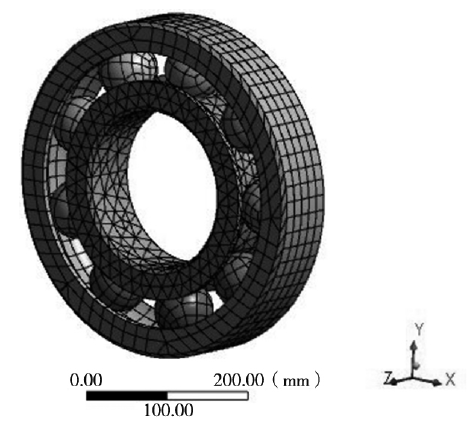
图1 . 深沟球轴承有限元网格模型
1.2、边界条件设定
在轴承运行过程中,其中内圈是与转子轴接触,外圈则一般是与固定件接触在一起,因此在设置深沟球轴承约束条件时将图 1 中轴承外圈设定为固定约束,内圈设定为旋转约束,本文转速设置为10000rpm。
1.3、有限元静应力结果
通过设定完结构的边界约束条件和网格模型后,在静应力模块中选中变形模块及平均应力模块,分析解算得到如图 2a 所示的静应力总变形和图 2b 所示的轴承平均应力云图。
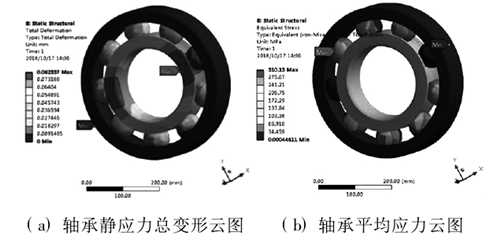
图2 . 轴承静应力应变形云图
从图 2 中的云图可知,深沟球轴承的最大变形量为 0.083mm,轴承的最大平均应力为 310MPa,由于在设定材料时,定义的轴承材料为是轴承钢,弹性模量为210GPa,屈服强度为 1667MPa。根据第 4 强度理论可以计算材料是否符合强度要求,强度公式为:
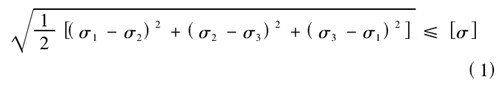
式中,σ1,σ2,σ3为 3 个法向的应力。在计算材料的许用应力时,安全系数一般取的是 1.5,通过许用应力公式计算可得到。许用应力公式:

通过结合式( 1) 与式( 2) 可以计算轴承的许用应力为 1111.3MPa。结合图 2 应力云图可得 310MPa≤1111.3MPa,所以创建的轴承结构的强度满足设计分析要求。因此在后续的谐响应分析及疲劳寿命的分析中可以获得轴承具有参考价值的数据参数,为后期轴承的改进提供有效的优化方案。
1.4、深沟球轴承模态分析
在绘制深沟球轴承结构的三维模型时,忽略掉一些对结构影响不明显特征,这样将能加快求解时间。由于轴承产生破坏的阶段主要是在负载工况下发生的,所以本文在继承静应力分析的基础上对轴承的模态振型进行研究分析。设定模态阶数为 6 阶,得到轴承的前 6 阶模态固有频率如表 1 所示。
表 1 深沟球轴承前 6 阶振型

结合 1.1 节的模态有限元分析可知,结构在运转过程中,主要是低阶模态的振型对结构的破坏较为关键,因此在有限元分析时不需要考虑到高阶模态的振型,因此选取了轴承的前 6 阶进行模态振型分析,模态分析结果如图 3 所示。
从图 3 中模态振型变化中可以得到,轴承的低阶模态振型变化量较大,主要对内圈的轴向振动变形较为明显,其中在模态 2 阶中振动变形达到最大,最大约为 20mm,可以判定在内圈与滚珠接触的部位较为薄弱,为提高轴承的可靠性及寿命可以在与轴承的内圈与滚珠接触部位提高加工精度或对滚道进行特殊处理,以提高滚道的光滑度及强度。对此在本文的后续谐响应分析中主要对轴承结构的内圈进行分析,为后续轴承结构的优化及加工提供参考。
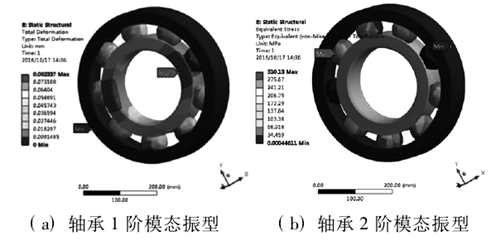
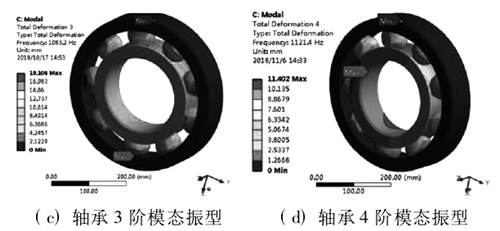

图3 . 深沟球轴承前6阶模态振型云图
1.5、深沟球轴承谐响应分析
结构的谐响应分析主要是对载荷在不同频率下的振动响应,直接与结构的载荷有关,而模态分析的结果只是单一的获得在某一频率下的振型变化,并不能获得在不同频率下的变形。因此结合模态分析结果搭建谐响应分析来提高谐响应分析结果的可用性,同时通过谐响应分析还可为轴承的疲劳破坏和共振破坏具有一定预测作用,对此本文通过模态叠加法开展轴承结构的谐响应分析,在求解中的设置条件为:
① . 设置轴承的边界条件参考 1. 2 节中的条件。
② . 从图 3 的模态云图和表 1 中的前 6 阶固有频率可知,轴承的第6阶频率为 1285.3Hz,对此设置谐响应的分析范围为0~1500Hz,同时为了提高计算结果的精确性设置求解步数为 100 步对应的有100个解。由模态分析可知变形主要发生在轴承的内圈,因此在谐响应分析中主要选取内圈进行了谐响应分析,通过求解计算获得了内圈沿 X、Y、Z 方向的位移变化情况,如图4所示。
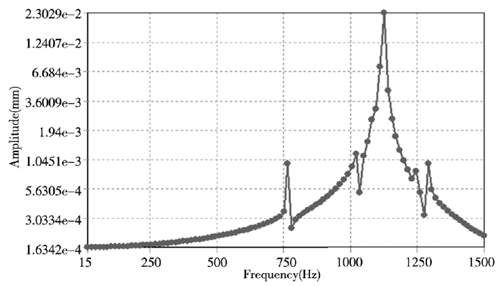
(a) X 方向
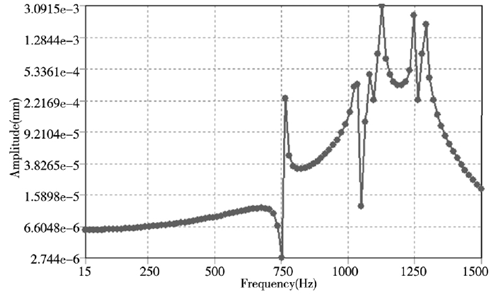
(b) Y 方向
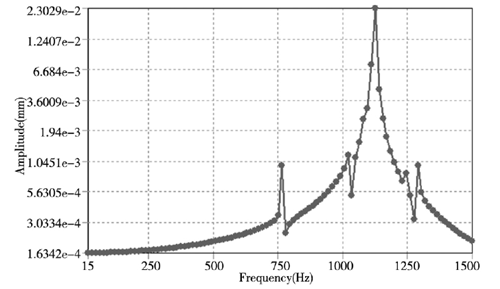
(c) Z 方向
图4 . 轴承内圈结构 X、Y、Z 方向位移响应曲线
从图 4 中的轴承内圈结构 X、Y、Z 方向位移响应曲线可知,轴承结构的位移响应随着频率的增加而增加,呈正相关。而在 X、Z 方向的位移在模态 5 阶( 约1125Hz) 时达到最大位移变化,最大变化量为0.023mm,而对于Y方向的位移变化量则较小为0.003mm,这要是轴承在 Y 方向上主要是受到径向的力,而 X 和 Z 方向还会受到沿 X 轴的轴向力,因此在 X和 Z 方向的位移较大,虽然 Y 方向的最大位移量没有X 和 Z 方向的大,但在频率从1阶到 6 阶范围内位移变形量较为均匀,因此造成的破坏不容忽视。通过对轴承的谐响应的分析可知 X、Y、Z 方向所造成的影响都不可忽视,在后期优化和加工工艺中通过设计特定的工装来优化轴承的结构,谐响应分析结果也为后期同类产品的优化提供参考。
2、深沟球轴承疲劳寿命分析
2.1、Hertz 接触应力计算
在分析轴承应力疲劳寿命时,应先分析轴承的应力,同时找到轴承的最大应力区域。对此依据 Hertz接触应力理论对轴承的应力进行分析,在接触应力中接触载荷 Q 与弹性趋近量 δ 满足下式:
式中,K 代表接触体之间的载荷变形系数,一般与接触体的材料及外形有关。
在轴承工作过程中,由于内外滚道的直径差异,滚道对滚珠的接触应力也有所不同,同时 2 滚道的法向趋近量等于滚珠分别与内外滚道趋近量之和,满足下式:
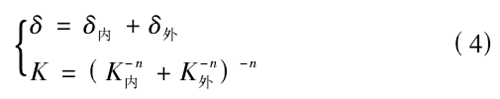
对于深沟球轴承,式( 3) 和式( 4) 中的 n 系数一般取 1.5。通过 Hertz 理论分析球轴承的接触问题,其最大的接触应力为:

式中,a 表示接触椭圆的长半轴; b 表示接触椭圆短半轴。
通过上式理论分析在结合图 2 所示的静应力仿真分析云图可知,接触处的正压力主要为滚珠与内外圈接触部位,其值沿曲面轴向与法向变化,与式( 5) 的接触理论分析一致。
2.2、疲劳分析
采用 ANSYS 联合仿真对深沟球轴承进行疲劳计算,在分析轴承静应力的基础上联合 Faigue 模块进行分析,在分析设置中为了提高分析的有效性,在搭建的Faigue 模块中设置疲劳强度因子为 0.8,通过反复模拟分析取最小基本载荷变化幅度和最大基本载荷幅度分别为 10% 、300% ,由此获得轴承结构的疲劳敏感性曲线如图 5 所示。
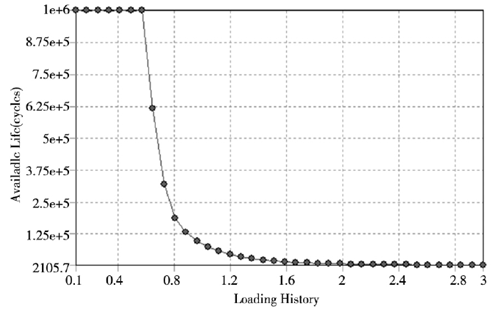
图5 . 深沟球轴承疲劳敏感性曲线
在设定轴承的疲劳安全因子分布云图命令,可获得如图 6 所示的安全因子分布云图。从图 6 中可以得到,本文选取的深沟球轴承最小安全影响因子为0.27795,最容易发生疲劳破坏的部位主要是轴承内圈,这与实际工况下的破坏一致,为提高寿命,在后续的优化设计可以改变内圈材料及内圈与滚珠接触处的尺寸参数来提高轴承内圈的使用寿命。由图 5 中的敏感性曲线可知,轴承在载荷变化幅度为 10% ~ 60% 范围内对轴承的寿命影响不大,但在载荷变化幅度超过200% 时则直接对轴承造成破坏不满足设计要求,通过上述分析可为轴承在设计中验证轴承疲劳寿命是否满足要求提供参考。
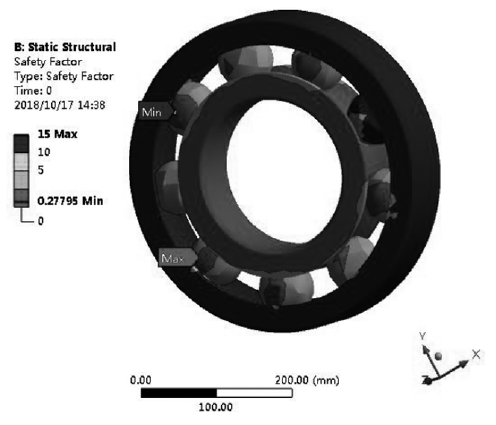
图6 . 深沟球轴承安全因子云图
2.3、振动疲劳寿命计算
一般情况下轴承的循环寿命较高,属于低应力高周疲劳,通过采用全寿命分析方法,即 S-N 曲线对轴承进行疲劳寿命分析计算,通过上述的对轴承的材料进行定义得到轴承的 S-N 曲线如图 7 所示。
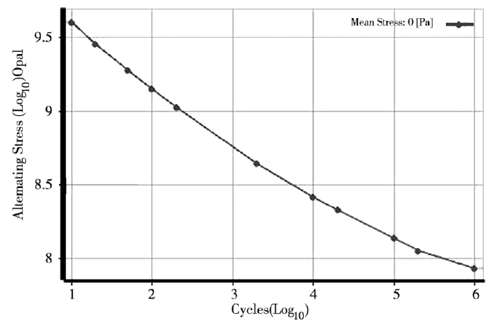
图7 . 轴承 S-N 曲线
在有限元分析中,设置雨流循环计数的方法对不规随机的载荷时间历程曲线进行转化成一系列恒定幅值的载荷,本文设定的载荷为恒定幅值载荷对轴承进行疲劳寿命预估,如图 8 所示。
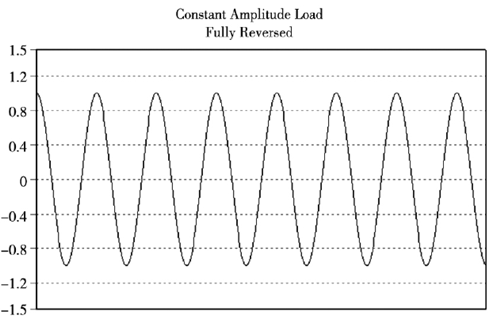
图8 . 恒定幅值载荷
其中疲劳寿命公式如下:
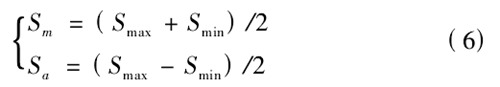
式中,Sm表示平均应力; Smax表示最大应力取310MPa; Smin为最小应力取 34MPa; Sa表示交变应力幅。
其中平均应力的修正应力公式为:

式中,Sn为平均应力 Sm的修正应力;
由图 7 所示的轴承 S-N 曲线来计算曲线间的斜率h,可以假设 S* N = C 为直线,利用最小二乘法来拟合出最优的直线方程,拟合得到如下方程:
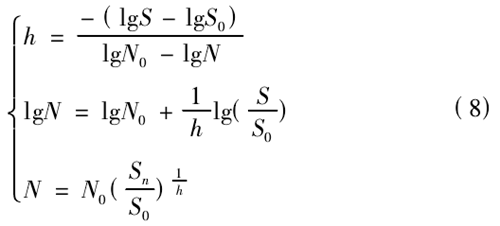
式中,N0表示循环次数,N0= 1 × 106; S0表示在 N0=1 × 106时的应力;
结合图7可知 lg N0= 6,lg S0= 7.88,lg N = 3,lg S = 8.75 ,通过计算可得到 h 值为 - 0.29。其中平均应力 Sm的修正应力为:Sn=153.8MPa 将其带入式(8) 中可得轴承疲劳寿命 N≈8.74 × 104次。结合图5的敏感性曲线图可知轴承的载荷变化幅度在 10% ~60% 范围内,因此对轴承的寿命影响不大,满足疲劳寿命设计要求。
同时借助有限元 Faigue 分析模块,对深沟球轴承循环次数的疲劳寿命进行求解计算,可获得图 9 所示的轴承疲劳寿命云图。
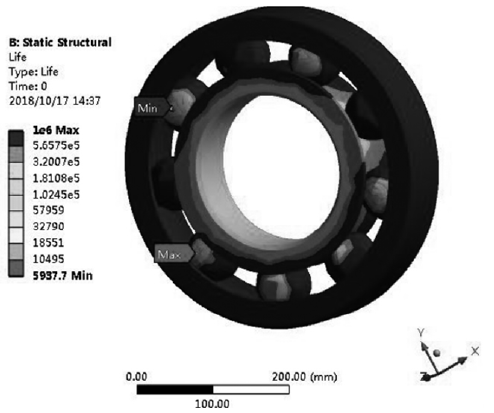
图9 . 深沟球轴承疲劳寿命( 循环次数)
由图 9 中的疲劳寿命分析云图可知,当工况条件为转速设置 10000rpm 时,轴承的寿命范围为 5937.7 ~1×106次,寿命较小处为轴承的滚珠外侧和轴承内圈部位,但是寿命薄弱处较少,其有限元疲劳寿命分析与理论计算结果大体一致,且有限元分析法能够将疲劳破坏点清晰直观的表示出来,由此可知通过利用有限元法对结构做疲劳寿命分析是可靠的,可为后续结构优化提供参考。
3、结 论
深沟球轴有限元静应力及模态分析,能获得结构的固有频率及振型变化,可为结构的谐响应及疲劳分析提供基础。
(1)、结合有限元静应力及模态分析结果,采用模态叠加法,搭建了轴承结构的谐响应分析模块,获得了轴承内圈沿 X、Y、Z 方向上的位移响应曲线,得到了轴承在 X、Z 方向的位移在模态 4 阶( 约1125Hz) 时达到最大位移变化,最大变化量为 0.023mm;
(2)、通过利用材料的 S-N 曲线理论以及 Hertz 接触理论开展了轴承结构的疲劳寿命分析,在静应力分析的基础上,通过 Faigue 模块建立轴承结构的疲劳分析模型,理论疲劳寿命为 8. 74 × 104次,与仿真分析结果大体一致,验证了仿真计算的可行性,也为轴承结构的后续优化提供参考,加快研发进度。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息





