基于 ANSYS-PDS 的数控导轨磨床主轴可靠性分析
2019-8-2 来源:泰州市产品质量监督检验院 作者:胡军
摘要:根据可靠性分析理论,运用有限元分析软件的概率设计功能(模块),对数控导轨磨床的主轴进行可靠性分析。分析时按照工程实际,将主轴的几何尺寸、载荷、强度极限等参数作为随机输入变量,采用蒙特卡罗法进行抽样计算,可以得到比传统设计方法精度更高的主轴失效概率。以 MK5220 数控导轨磨床主轴为例进行计算,结果表明利用 ANSYS/PDS 模块对磨床主轴进行可靠性分析是可行的。
关键词:数控导轨磨床;主轴;蒙特卡罗法;可靠性
数控导轨磨床的关键结构是传动结构,主轴是传动结构的关键零部件,它的工作状况直接影响数控导轨磨床的加工质量,制约着磨床的发展。主轴直接承受来自电机的扭矩,而且在实际工况下,磨床的加工环境是恶劣的,主轴很容易产生各种故障,甚至损坏。因此,为提高磨床主轴的性能,可以对其进行可靠性分析。可靠性分析方法可以将影响零件工作性能的变量(如尺寸、载荷)视为不确定量,从而分析这些变量对零件可靠性的影响,进而提高零部件设计的准确性和可靠性。本文就是根据文献运用 ANSYS-PDS 模块对实际工况下的磨床主轴进行可靠性分析。
1 、磨床主轴可靠性分析过程及理论
1.1 基本原理
可靠性工程是综合型的系统工程,产品的可靠性与其设计、制造、使用等环节密切相关。其可靠性设计是以应力—强度干涉模型为基础。一般情况下,用 Y 表示施加在产品上的物理量,如载荷,称为产品所受的应力;用 X 表示产品能够承受这种应力的能力,称为产品的强度。要使产品在规定的时间内可靠的工作,就必须满足 Z=X-Y≥0。其中,应力、强度都是某些变量的函数。产品的可靠度 R 就是 Z 值大于等于零时的概率。在磨床主轴可靠性分析中,将实际工况下的许用应力值与最大应力值的差值定义为 Z,那么,主轴的可靠度为 R=P(Z≥0)[5]。
1.2 主轴可靠性分析基本过程
本文运用 ANSYS-PDS 模块对磨床主轴进行可靠性分析,根据 GB/T 9061-2006 中的相关要求,对磨床主轴在最大扭矩工作状况下作可靠性分析。具体分析流程如下:
(1)创建主轴的可靠性分析文件,包括建立主轴模型,施加载荷、约束及求解等过程;
(2)对主轴进行可靠性分析,其中包括定义随机变量,选择仿真循环次数等过程;
(3)可靠度的求取。
1.3 主轴可靠性分析方法
在 ANSYS-PDS 分析过程中,常用的概率设计方法有蒙特卡罗法和响应面法。蒙特卡罗法对有限元有非常好的适应性,能模拟实际问题的真实特征。本文采用蒙特卡罗法进行可靠性分析。
2 、磨床主轴的可靠性分析
2.1 主轴受力分析
主传动系统工作情况如下:电机(额定功率为 30 k W,额定转速为 1470 r/min,经传动比为 150:290 的带轮带动主轴运动,主轴另一端连接砂轮,砂轮尺寸为Φ600×150×Φ305 mm。数控导轨磨床在运行过程中,其主轴转速范围为 600~1100 r/min,磨削深度为 0.02~0.1 mm。主轴模型简化图如图 1 所示。主轴材料为45#钢,许用扭转切应力为 30 MPa,安全系数取 n=2。
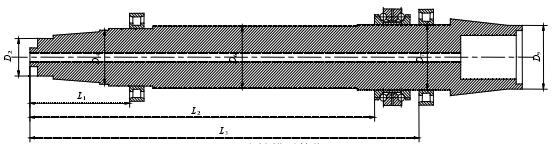
图 1 主轴模型简化图
根据文献中的有关规定,机床在检验时需做负荷试验,包括机床主传动系统扭矩试验,主传动系统最大功率试验等。由于磨床主轴工作时主要受扭矩作用,且主轴在最大功率下运行时所受扭矩小于最大扭矩试验中主轴承受的扭矩,因此本文主要研究最大扭矩条件下主轴的可靠性。
按照该标准中最大扭矩的近似计算法,最大扭矩的公式为:
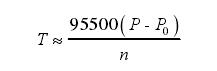
式中:T 为扭矩,N·m;P 为切削时电动机的输入功率,k W;P0为机床装有工件时的空运转功率,k W;n 为机床主轴转速,r/min。计算得 Tmax=540 N·m。按 125%计算得出进行可靠性分析时 T=680 N·m。磨床在一般情况下磨削时,磨削深度 ap=0.05 mm,主轴转速为 750 r/min,工件速度为20 m/s。由于磨削力受多方面因素影响,没有准确的公式计算,在本文中运用平面磨削力的经验公式计算得出切向磨削力:
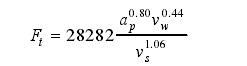
按照 Fn/Ft=3.8 求出磨削时所受的径向磨削力。经计算得:Ft=282 NFn=1071.6 N
2.2 主轴建模、网格划分及加载求解
采用 ANSYS 参数化设计语言 APDL 对主轴进行建模,建模过程中在不影响主轴受力的条件下对其进行了一定的简化,忽略了主轴的倒角等。选用 4 节点的平面单元模型 Quad 4node 182 先对主轴截面进行网格划分,再旋转得到主轴的网格划分图,如图 2 所示。然后对主轴分别施加边界条件和载荷,再进行求解。其中扭矩及径向力均施加在对应节点上。最大扭矩下,施加约束及载荷后求得的主轴应力云图如图 3、图 4 所示。

图 2 主轴有限元模型

图 3 主轴最大扭矩试验应力图
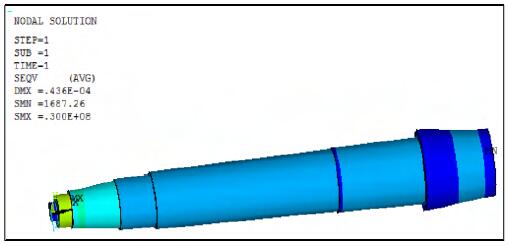
图 4 主轴正常切削应力图
2.3 可靠性计算与分析
分别整理保存分析求解过程的命令流。写入可靠性分析文件。将等效应力按降序排列并提取最大等效应力值“maxstress”,然后定义极限状态方程,即求出强度与最大应力值的差值,将之与之前ANSYS应力分析命令一起构成概率分析文件。进入 PDS 模块,读取保存的可靠性分析宏文件,选择、定义随机输入变量(见表 1)和输出变量服从的分布类型及其参数。
表 1 随机输入变量统计表
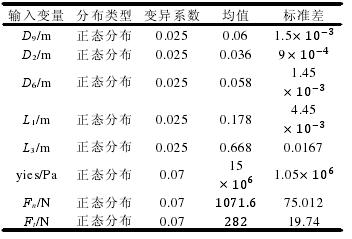
2.4 可靠性分析结果
选择蒙特卡罗法进行概率设计,选择拉丁抽样法,模拟样本次数为 60 次,通过计算可得到主轴在许用扭转切应力为 20 MPa,置信度为 95%时,主轴在最大扭矩试验时可靠度为 85.97%。
3 、结论
本文采用可靠性分析理论及 ANSYS/PDS模块,根据工程实际及国家标准的相关规定,采用蒙特卡罗法,以 MK5220数控导轨磨床主轴为例,进行可靠性分析,分析计算得到了其在最大扭矩下的可靠度。通过ANSYS/PDS 定量的计算出磨床主轴在恶劣工况下的可靠性。同时这种分析方法具有普遍适用性,可以对类似机械零件进行可靠性分析,在工程应用中,具有一定的实用价值。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息





