机床主轴温度测点的 K-means 优化及试验
2019-7-26 来源:南通大学 南通第五机床有限公司 作者:周成一 庄丽阳 袁江 高传耀
摘 要:针对机床热误差补偿技术中温度测点的优化选择,提出一种基于 K-means 算法和 Pearson 相关系数相结合的方法。通过 K-means 算法将不同位置测点的温度进行聚类,用 Pearson 相关系数计算温度与主轴热误差之间的相关性,从每一类别中选出一个最优测点组成最优测点组合,并对最优测点处的结果进行热误差建模。在立式加工中心 VMC850E上对该方法进行了试验验证,将温度测点的数量由 8 个减少至 2 个。经方差分析和 F 检验,验证了最优测点处的温度与热变形之间显著线性,模型可靠。
关键词:主轴;K-means 算法;Pearson 相关系数;测点优化
1 、引言
在实际生产过程中,机床零部件的发热最终会导致主轴在轴向产生偏移,对产品的加工精度造成影响,甚至产生报废品。大量研究表明,机床热误差已经取代几何误差,成为最主要的误差源,减小热误差已经成为企业亟待解决的问题之一。
热误差补偿技术相比机床结构改进,是减小热误差、提高加工精度的更加有效、经济的方法而温度测点的优化布置是实现热误差补偿的重点,其优化结果的有效性大大影响着热误差补偿的精度。近年来,国内外学者提出了热误差模态分析法、逐步线性回归法、模糊聚类法、神经网络法等多种温度测点的优化布置方法。
但上述测点优化布置方法有的过程简单,但十分不准确,影响热误差模型的准确性;有的过程十分复杂,而且需要大量的样本,耗费大量的时间和成本,从而限制了这些方法在热误差建模与补偿中的应用。K-means 聚类是一种经典算法,其拥有效率高,分类明显,能对大量数据进行分割聚类等特点。
该算法通过不断寻找新的聚类中心,使得聚类效果评价函数 J 不断收敛,直至聚类不再变化,达到较优的聚类效果。将其与 Pearson 相关系数相结合,对机床主轴温度测点进行优化。该法在对机床主轴进行热态特性分析的基础上,采用 K-means 算法对热敏区域测点的温度特征聚类,再通过 Pearson 相关系数选出与热变形相关性最大的测点,实现主轴温度测点优化。
最后,对最优温度测点进行热误差建模,并利用方差分析和 F 检验验证模型的可靠性。
2 、温度测点优化
2.1 热态特性分析
在将主轴导入 ANSYS Workbench 进行热态特性分析之前,为减小分析处理时庞大的计算量,需要对主轴结构进行合理简化,简化有如下几点:(1)去除一些对模型热特性影响较小的特征(如倒角、小孔等);(2)主轴及箱体结构中的一些腰型孔、小通孔、螺纹孔等均按实体处理;(3)打刀缸及其附属部件不在分析范围内;(4)主轴上的小配件不在模型中显示。
完成主轴模型的简化后,根据所选机床的实际情况,确定热态特性分析的主体为主轴以及主轴箱。主轴的热传递方式包括热传导、热对流以及热辐射。而此款立式加工中心主轴在冷却液等的作用下,温升较小,故忽略通过热辐射失去的热量,热传递方式只考虑热传导和热对流。其中,热传导系数由主轴及箱体的材料决定,而热对流主要考虑套筒内冷却液的强迫对流换热、主轴旋流带动周围空气的流动形成的强迫对流换热以及空气的自然对流。
由此可计算得主轴的热边界参数,如表 1 所示。
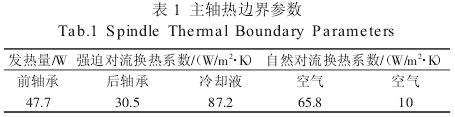
将上述已知参数在有限元分析软件中进行设定,并进行温度场仿真,通过稳态热分析结果划定出具体的热敏区域。主轴及箱体系统的稳态热分析结果,如图 1 所示。根据仿真结果,得知稳定后主轴最高温度位于前端轴承,约为 32.9℃,其次为后端轴承,约为 30.3℃,即热敏区域为前后轴承之间的区域。利用该软件中的 Probe 探针,结合实际尺寸,初步确定热敏区域范围为[88mm,265mm]。

2.2 K- me a ns 算法温度聚类分析K-means 聚类算法是一种基于划分法的聚类算法,它将聚类温度集内的所有温度样本的均值作为该聚类的中心点。其工作原理是首先从温度测点集合中随机选取 k 个温度测点作为初始聚类中心,分别计算各个温度测点到初始聚类中心的相似度(以欧式距离作为相似度测量准则),并根据计算所得的距离将每个温度测点赋给最近的聚类中心。
然后再计算该温度测点集合内的所有温度的平均值,得到新的聚类中心。反复循环计算,一旦连续两次循环得到的聚类中心均为同一个温度测点,说明温度聚类分析完成。通常采用平方误差函数 J 作为聚类效果的评价函数,公式如下:

式中:P—温度分类 Cj中任一个温度测点;Z—温度分类 Cj的温度聚类中心,算法流程如下:(1)参数设定。随机选择 k 个温度测点作为初始温度聚类的中心;(2)初始聚类。计算并比较温度测点到每一个温度聚类中心的距离,并根据最短距离聚类;(3)修正聚类。根据新的温度聚类,计算该温度聚类的平均值;(4)聚类结果。若温度聚类中心未发生变化,输出最终聚类结果,循环结束,否则,返回步骤(2)继续迭代。
2.3 相关性分析
相关性分析是用来研究变量间关联程度的一种统计方法,采用相关系数来表征。这里通过比较温度测点与热误差之间的Pearson 相关系数,来选出温度聚类结果中每一类别里的最优测点。相关系数 r 越大,则表明两者间相关性越强。公式如下: 文2 式中:X—任意一个温度测点的数据;Y—热变形数据。
3 、试验验证
3.1 实验方案
以 VMC850E 高速高精密立式加工中心的主轴作为实验对象,如图 2 所示。在前端轴承与后端轴承之间的热敏区域,均匀布置 8 个温度传感器,并在主轴轴向延长线上布置一个激光位移传感器。采集数据时,8 个温度传感器分别将采集的温度信息和标签信息打包无线发送给读写器,上位机通过自编的 Lab VIEW 串口调试程序接收温度信息和标签信息,实现信息的无线采集,最大程度上解决了一般测试方法布线繁杂等问题;而激光位移传感器将主轴轴向的热变形数据通过专用的控制器传输给上位机。
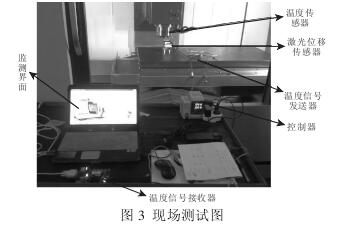
实验时,设定立式加工中心主轴转速为 3500r/min,运转120min,并通过自编 Lab VIEW 软件对温度传感器及激光位移传感器同步发送命令。采样间隔为 3min,并对采集的各测点温度数据和轴向热变形数据实时显示、存储。实验现场测试图,如图 3所示。
3.2 测点优化结果
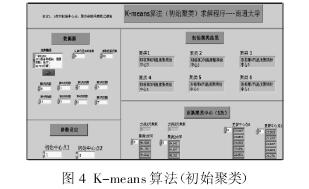
将采集得的 8 个测点的温度数据与主轴轴向的热变形数据,首先输入到 K-means 算法(初始聚类)Lab VIEW 求解程序当中,设定初始聚类中心个数为 2 个,分别为第 1 列和第 3 列温度数据,初始聚类结果,如图 4 所示。
由初始聚类程序计算结果得,第(1、5、6、7)列温度数据分为一类,第(0、2、3、4)列温度数据分为另一类,并根据初始聚类的结果,求出更新中心点 0 和更新中心点
1。
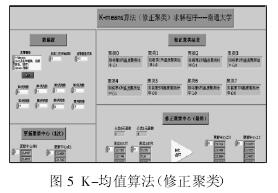
再将更新中心点 0、1 和 8 个测点的温度数据输入到 K-means 算法(修正聚类)Lab VIEW 求解程序当中,如图 5 所示,经过多次修正,求解出最终的更新聚类中心 0’、1’,最终聚类结果为第(1、3、5、6、7)列温度数据分为一类,第(0、2、4)列温度数据分为另一类。
最后,由于选择的初始聚类中心对于最终聚类结果有着很大的影响,且为了达到较好的聚类效果,需要选择不同的初始聚类中心,分别输入 K-means 算法求解程序中,比较其误差平方和,得出最优分类结果。
结果,如表 2 所示。
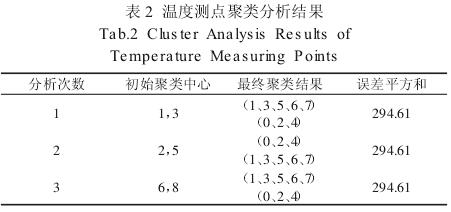
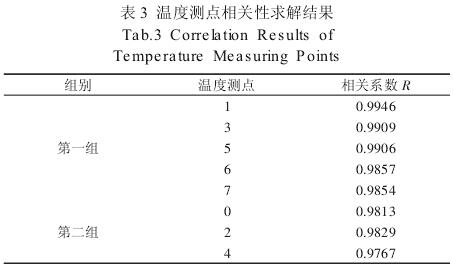
由上述结果可以看出,由三组初始聚类中心进行聚类分析的最终结果相同,则以此聚类结果作为最佳聚类结果。再利用 Pearson 相关系数计算各温度测点数据与热变形数据之间的相关性,从每一类中选出对热变形影响最大的一个点。求解结果,如表 3 所示。
第一类(1、3、5、6、7)中 1 号测点与热变形之间的相关性最大,第二类(0、2、4)中 2 号测点与热变形之间的相关性最大,由此可知,经优化后的最佳温度测点组合为(1,2)。
4 、回归建模及分析
将最佳温度测点组合(1,2)的温度数据和轴向热变形数据输入到热误差建模程序中求解,并通过方差分析和 F 检验法对模型预测能力进行评价。设温度值 x1、x2与热变形值 y 之间满足如下函数关系:
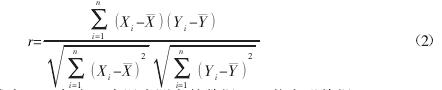
中:x1、x2—测点 1、2 的温度数据;y—轴向热变形数据;a、b、c—回归系数。若将温度数据 x1和 x2代入式(3)即可得到相对的热变形值y。利用最小二乘法,建立误差方程并转化为正规方程,最终矩阵化求解。为避免繁杂的计算过程,利用 Lab VIEW 图形化软件开发界面友好的热误差模型求解程序,结果,如图 6 所示。
由图 6 可以看出,所得的热误差模型为 y=0.00061x1+0.00136x2-0.01055,且在给定显著水平 0.01 下,回归方程 F> F0.01(2,40)=5.18,即在最佳温度测点处监测的温度与热变形有显著的线性关系,该回归方程可较好地反映出热变形的客观变化规律。
5 、结论
(1)合理简化主轴及箱体结构,导入 ANSYS Workbench 进行稳态热分析,得出热敏分析图,利用主轴实际尺寸确定热敏区域范围为[88mm,265mm]。(2)采用 K-means 算法对热敏区域测点的温度特征聚类,再通过 Pearson 相关系数选出与热变形相关性最大的测点,有效地热敏区域内监测主轴及箱体温度的 8 个温度测点减少到 2 个,极大地降低了热误差建模的时间和成本。(3)对优化后的温度测点和热变形进行热误差建模,并利用方差分析和 F 检验验证,该模型可较好地反映出热变形的客观变化规律。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com





