高速高精度电主轴温升预测模型
2018-10-17 来源:转载 作者: 张丽秀 李超群 李金鹏 张珂 吴玉厚
摘要:提出高速高精度电主轴温升预测模型,将有限元模型与试验数据相结合,精确预测不同工况下电主轴的温度场。建立电主轴流场、温度场有限元模型,分析冷却系统及润滑系统参数对电主轴温度场的影响;考虑电主轴运行速度、载荷,设计电主轴损耗测试方法,将测得的电主轴总损耗作为计算电动机、轴承生热依据;考虑冷却系统、润滑系统参数及环境条件对换热系数的影响,采用最小二乘算法,基于电主轴表面温度测试数据,优化电主轴换热系数,并将优化后的换热系数作为有限元模型的边界条件。建立 170SD30-SY 电主轴温升预测模型,将换热系数优化前后的温度场仿真数据分别与试验数据对比。结果表明,换热系数优化后的温升预测模型预测的精度提高了 4.78%,提出的电主轴温升预测模型有较高的预测精度。
关键词:电主轴;温度场;换热系数;最小二乘法;有限元
0、前言
电主轴单元是数控机床的心脏,是保证机床工作精度的关键部件,其技术的高低、性能的优劣以及单元的配套水平,都决定和影响着数控机床的发展速度。而目前难以解决的问题是,电主轴高速运转过程中会产生大量的热量,导致不均匀的主轴零件热膨胀或刀具变形,影响电主轴的精度甚至轴承的预紧力,进而影响机床的加工精度及使用寿命。因此电主轴的未来发展必然要求对温升、热变形等方面实现精准预测与控制,实现电主轴的自动化和智能化,提高机床主轴自主创新能力。同时,研发高精度、高转速的智能电主轴单元也是航空航天、汽车、精密模具等尖端产品制造领域实现智能制造的前提。
近年来,电主轴热特性在主轴工作中的重要影响引起了国内外专家的研究热潮,并取得大量的成果。重庆大学的陈小安等提出一种采用功率流模型计算电主轴电磁损耗、轴承损耗和风阻损耗间的关系,并在此基础上对主轴温度场进行分析,认为电动机定、转子和轴承部位的温升较大,应重点控制;西南科技大学曾宏强等采用热-结构耦合的方法分析出主轴热变形是影响加工精度的一个重要原因;上海交通大学的杨建国等采用自主研发的数控机床误差在线实时补偿系统,使机床主轴热漂移误差减小 90%以上;MANSINGH等运用三维流体数值分析的方法模拟不同冷却管道下水冷系统对高速电主轴温度场分布的影响,得出循环冷却水道可以更有效的降低电主轴温度;HOLKUP 等分析了因瞬间温度变化而引起轴承与链接部件的损坏;德国学者 UHLMANNA 等预测高速电动机主轴热特性时,考虑了复杂的边界条件如:热源接触传热和主轴部件之间的对流传热,并进行了验证性试验。上述国内外有关电主轴热特性研究主要具有以下三个特点:①根据电动机额定功率或功率流模型来计算额定损耗;② 通过经验公式计算电主轴各部件的换热系数;③ 集中在热态模型的建立及分析热源的产生机理。
本文首先通过损耗试验精确测得电动机损耗数据,采用最小二乘法对各换热系数进行优化,在此基础上运用有限元分析软件建立电主轴温升预测模型,仿真 170MD30-SY 型电主轴在 12 000 r/min下的空载瞬态温度场;并通过电主轴温升试验,验证所采用方法的有效性及所建模型的准确性,最终为智能化电主轴系统的设计和开发提供重要的理依据。
1、 高速电主轴的生热和传热分析
1.1 电主轴生热机理
电主轴在高速运转时会产生大量的热,主要有两个热源,一是主轴内装式电动机的损耗发热,二是主轴轴承的摩擦生热。电主轴运行的主要特点是变频器供电,运转速度及载荷变化频繁。变频器供电使电主轴电动机由于电磁谐波而产生谐波损耗,因此主轴电动机的发热不容忽视;高速变载运转使轴承摩擦发热影响因素更为复杂。
在电主轴温度场分析中,通常采用经验公式计算电动机损耗及轴承摩擦损耗,但实际工作中电主轴并不完全工作在额定功率下,且效率不是恒定不变的,因此用各种计算公式所得损耗会产生较大误差。
1.2 电主轴的换热机制
为了减小电主轴发热而导致的热变形,电主轴单元在使用过程中通常采用水冷系统冷却电动机定子;并采用油-气润滑方式润滑轴承,同时压缩空气可以降低转子表面及轴承的温度。电主轴内部换热机制非常复杂,其换热形式如图 1 所示,即轴承表面与压缩空气的强迫对流换热、转子转动引起的端部空气强迫对流换热、压缩空气通过定转子间隙的强迫对流换热、冷却水流过定子表面的对流换热及电主轴表面的自然冷却换热。考虑电主轴各部分温差小于 50℃,可以忽略热辐射的影响。
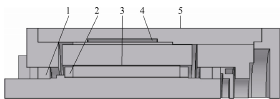
图 1 电主轴各部件换热类型
1. 轴承表面与压缩空气的强迫对流换热
2. 转子转动引起的端部空气强迫对流换热
3. 压缩空气通过定转子间隙的强迫对流换热
4. 冷却水流过定子表面的对流换热
5. 电主轴表面的自然冷却换热
通过对电主轴生热机理和换热机制的分析可得出如图 2 所示的电主轴系统温度场分析的原理图。电动机和轴承的生热量是通过热传导的方式传至电主轴其他部位,由于其传导速率主要与材料属性和电主轴各部位温度差等有关,故本文不考虑从热传导的角度提高温度场的预测精度。从图 2 中可以看出,在热源一定的情况下,可以对冷却系统参 数及其结构和油-气润滑系统参数及其结构两方面进行优化,从而可得出更为精确和使电主轴温升最小的换热系数值,进而建立精确的电主轴温度场模型。
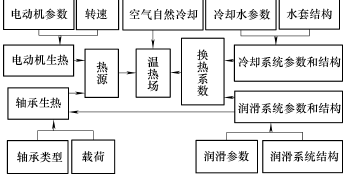
图 2 电主轴系统温度场分析原理图
2、高速高精度电主轴温升预测模型
2.1 基于损耗试验的电主轴生热量计算
为了较精确获得电主轴电动机生热量和其轴承生热量,本文采用如图 3 所示的电主轴加载及性能测试系统测试电主轴电动机损耗及轴承摩擦损耗,具体步骤如下。
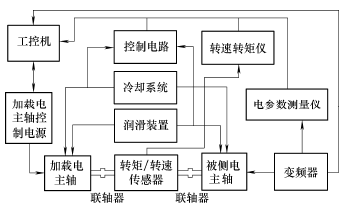
图 3 电主轴加载及性能测试系统
(1) 将加载电主轴与被测电主轴连接,切断被测电主轴电源,由加载电主轴带动被测电主轴旋转,即保持被测电主轴与加载电主轴同步旋转,此时认为被测电主轴只有摩擦损耗,测量加载电主轴的输入功率为 PJ1。
(2) 将被测电主轴与加载电主轴断开,加载电主轴独自空载至上一步相同的转速,测量加载电主轴的输入功率为 PJ2。
(3) 保持被测电主轴与加载电主轴断开,被测电主轴空载运行至上一步相同转速,电参数测量仪测出被测电主轴的输入电压和电流,则可求出被测电主轴的输入功率为 Pin。转矩转速传感器可测量出被测电主轴的输出转矩和转速,则可求出被测电主轴的输出功率为 Pout。则被测电主轴的摩擦损耗为f J1 J2p P P , 被 测 电 主 轴 的 电 动 机 损 耗 为e in out fp P P p 。
利用上述方法,测得 170SD30-SY 电主轴的摩擦损耗为 98 W,电动机损耗为 471 W,测试装置如图 4 所示。理想情况下,损耗全部转化为热量,当电动机高速运转条件下,有近 1/3 的电动机发热量是由电动机转子产生,其余 2/3 热量产生于电动机的定子。
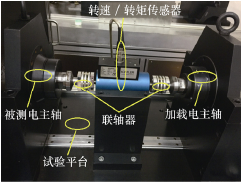
图 4 电主轴自动加载装置
一般情况下,损耗与负载有关,负载越大,损耗越大。由于本文旨在提供一种提高电主轴温度场预测精度的方法,将损耗作为引起主轴温升的主要因素,并通过损耗计算生热量后加载到有限元模型中,此处只将空载损耗数据作为计算实例。不同负载下的损耗均可通过本文试验装置测得。
2.2 基于最小二乘法的传热系数优化方法
最小二乘法是一种在多学科领域中获得广泛应用的数据处理方法,实际应用中,常采用最小二乘法利用试验数据来得到优化或相对理想的参数值,所以本文选用最小二乘法对电主轴各部位换热系数进行优化。图 5 为利用最小二乘法获取精确电主轴温度场预测模型流程图。首先通过试验获得电主轴某工况下的试验温度;然后采用传统算法对该工况下的各部分换热系数值进行计算,得出换热系数初始值;并将换热系数初始值加载至有限元模型,得出电主轴初始温度场分布;分别提取试验与仿真对应位置的温度数据;运用最小二乘法求出各部换热系数的最优值,将转换热系数最优值输入电主轴温度场有限元模型进而得出精确的电主轴温度场。
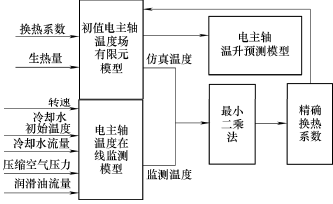
图 5 电主轴温度场预测模型
(1) 导热理论基础。电主轴稳定工作时,由于各部位的换热遵循能量守恒定律,所以热量从热源轴承、定子和转子通过热传导传至各个部件,以及电主轴零部件与空气和冷却水等介质之间通过对流换热散出是守恒的。对于热传导,根据傅里叶定律得,传导热通量与温度梯度间的关系为




图 6 电主轴温升测试装置
2.3 温度场模型及其优化仿真分析
本文针对 170SD30-SY 电主轴,考虑电动机和轴承发热利用三维模型进行仿真分析。在保证计算精度的前提下,将一对角接触球轴承、转子、定子等简化后装配在主轴上,忽略所有的螺钉、通气孔、通油孔及其一些细小结构,建立电主轴的温升预测模型。为了与传统建模方法对比分析,还采用传统经验公式计算获得电主轴内部换热系数。计算中假设电主轴运行条件:①环境温度23 ℃;② 油-气润滑系统润滑油采用 32 号汽轮机油,压缩空气进口温度 18 ℃,进口压力 0.365 MPa;③水冷系统进水口温度 20 ℃,冷却水流量 0.32 m3/h;④ 空载转速为 12 000 r/min。根据上述条件,获得表 1 所示的用于温度场仿真的换热系数。

表 1 温度场仿真边界条件
2.3.1 电主轴冷却润滑系统模型及仿真
为了分析电主轴的温升状态,首先需要建立电主轴定子水冷系统模型及轴承油气润滑模型。由于电主轴内部结构较复杂,为了简化求解过程,对油气润滑系统采用二维模型仿真;简化后的电主轴各部件大都为对称的回转体,因此,采用规则的四面体 和 菱 形 进 行 较 细 化 的 网 格 剖 分 , 图 7 为170SD30-SY 电主轴内部冷却润滑系统模型网格剖分图;将换热系数作为温度场预测的边界条件加载至模型可得出如图 8 所示的电主轴 x、y 和 z 三个方向的传导热通量云图以及如图 9 所示的水冷系统温 度场和电主轴温度场;将冷却水及压缩空气的参数加载至水冷系统模型和油气润滑系统模型可得出如图 9a 所示的冷却水流场,图 9b 所示的水冷系统温度场,图 9c 所示的压缩空气流场合和图 9d 所示的主轴温度场。
从图 9 流场和温度场可以看出,电主轴内部在冷却水及油气润滑的作用下,主轴外表面及定子的温度下降明显,但是转子的温度依然较高,因此精确的温度场预测对电主轴性能提高是必要的。
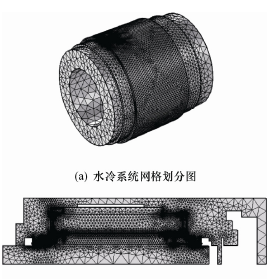
图 7 170SD30-SY 电主轴内部冷却润滑系统模型网格划分图
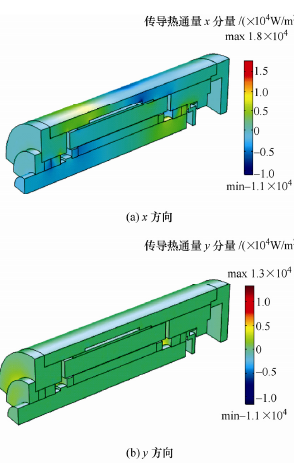
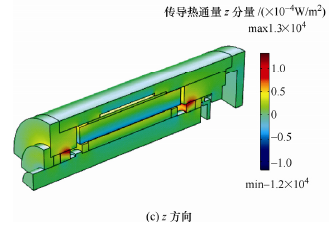
图 8 电主轴传导热通量云图

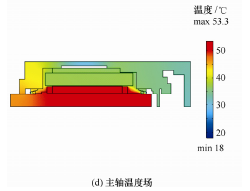
图 9 170SD30-SY 电主轴温度场
2.3.2 电主轴温度场优化仿真
在传统的电主轴热模型中,电主轴各部位的传热系数均采用经验公式计算得到,但实际上,不同电主轴间存在个体差异性,因此采用经验公式获得的换热系数也会给预测模型带来误差。本文利用实测温升试验数据,采用最小二乘法对换热系数进行优化,以此获得电主轴的温升预测优化模型。 温度测试试验过程如下:① 初始时,打开水冷控制系统和油-气润滑控制系统电源。将空气压缩机压力调至 0.72 MPa,压缩空气进入轴承压力调至0.365 MPa,进气温度 18 ℃,进水口温度 20 ℃,流量 0.32 m3/h;② 在空气压力达到 0.72 MPa 时,打开电主轴测试系统,设置主轴转速 12 000 r/min,空载运转。考虑到主轴尺寸小,空间的局限性问题,分别在电主轴热源位置,即前后轴承位置及两轴承跨距中间的定、转子位置布置共计 30 个温度传感器,传感器位置布置示意图如图 6 所示;采用图 6所示温升测试装置对电主轴各部位进行温度测量,并运用红外温度测量仪测量轴头温度变化。表 2 为用于换热系数优化的实测温度样本数据。
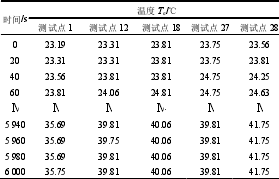
表 2 换热系数优化实测温度样本数据
为更直观地观察电主轴温度场及节省计算时间,优化后的模型取三维模型的 1/4。图 11 为换热系数优化前后电主轴温度场。比较图 11a、图 11b中电主轴温度场云图看出,优化前后电主轴各部分温度有明显变化。
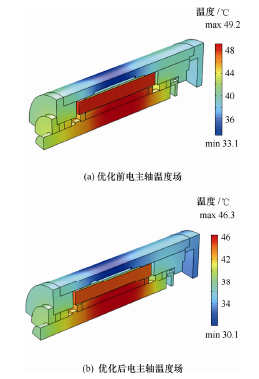
图 11 电主轴瞬态温度场云图
3、试验验证
为了验证优化后模型预测精度,选取该组试验数据中其他四组测试点温度做为预测模型检验数据,如表 3 所示,并将对应测试点的电主轴优化前后的仿真预测温度数据分别与这四组实测数据对比,获得图 12 所示的电主轴关键部位优化前后温度与试验温度对比图,以检测预测模型的准确性。
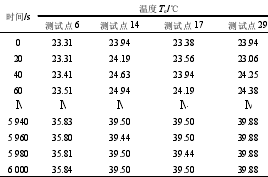
表 3 预测模型检验温度数据
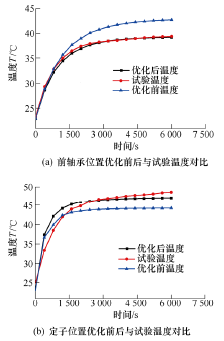
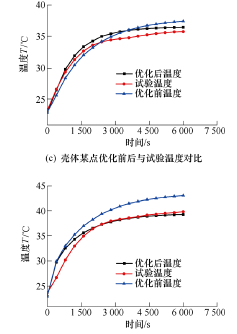
图 12 电主轴关键部位优化前后仿真温度与试验温度对比图
从图 12 可以得出,优化前预测的电主轴温度场平均误差为 2.71 ℃,相对误差为 7.12%;优化后预测的电主轴温度场平均误差为 0.89 ℃,相对误差为 2.34%。
4、结论
(1) 利用损耗试验所测数据对电主轴温度场进行预测,可显著提高电主轴温升预测精度。
(2) 在对各换热系数进行优化的基础上对电主轴温度场进行预测,优化后电主轴温度场预测的平均误差降低了 1.82 ℃,相对误差精度提高了 4.78%。
(3) 本文建立的电主轴温升预测模型,可为电主轴的温升智能控制提供依据。
来源:沈阳建筑大学机械工程学院 沈阳建筑大学高档石材数控加工装备与技术国家地方联合工程实验室
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息





