摘要：为了更好地实现螺旋锥齿轮精密数控加工，结合螺旋锥齿轮加工特点，在欧式线性空间中建立了数控加工模型及误差补偿模型。补偿模型为二级补偿机制，以齿面误差作为判断依据，通过对机床安装调整误差的补偿和加工过程中运动误差的补偿及时修正加工质量。由此，通过逐齿动态补偿，使得加工过程中机床误差得到修正，齿面加工精度得到提升。经仿真实验验证，该方法可实现连续轨迹运动中的多轴协调，有效提高螺旋锥齿轮数控加工机床的加工精度。
  
   
      ０　引言

     螺旋锥齿轮是空间自由曲面，需要五轴、六轴联动加工，加工误差具有实时变化的随机性且对齿面不同部位误差的影响也有大小和正负之分 。理论齿面上任意一点的齿面误差可以认为是机床各轴微小变化引起的齿面误差的叠加 。
 
 
      在车间中，通常采用离线误差测量而后依据经验手动调整的方法对初始齿坯安装和机床定位参数进行定性修正。随着数字化制造理论与技术的发展，齿面误差补偿研究多集中在初始安装参数对接触区形状位置的影响分析上 。
 

     但在实际加工过程中，不确定影响因素所引起的实时加工路径变化对齿面精度存在很大影响。可是，受机床结构的影响，在螺旋锥齿轮加工机床上建立实时补偿系统很困难。例如，五轴或六轴耦合运动增加了反馈补偿算法的复杂度；加工空间小妨碍了实时监测设备的安装调试。
 
  
     为此，本文采用机床精度设计和运动学标定两种途径对齿轮产品精度进行初步估算，在已有安装误差补偿基础上建立一种可实时监控反馈调整的机床控制策略，以提高系统动态特性，增强各轴间运动协调与参数匹配能力，实现螺旋锥齿轮精密数控加工。

  
  
     １　基于集合理论的精度分析方法

     定义１　集合Ａ 为映射ｆ 的定义域，记为Ｄ（ｆ）。

     
  
     使用基于集合理论的精度分析方法，可将螺旋锥齿轮精密数控加工误差补偿方法描述为：建立对加工过程误差的补偿策略，以缩小定义域Ａ的波动范围，经过函数ｆ映射，得到最小的产品质量波动空间Ｂ。定义域的波动空间由两部分误差造成：一部分为安装调试过程各轴的安装误差，另一部分为动态加工过程中各轴的重复定位误差。

     ２　螺旋锥齿轮数控加工模型

     本文选取国产ＹＫ２２７５数控铣齿机（图１）为对象，以格里森齿制螺旋锥齿轮滚切法数控加工大轮为例，进行具体研究。数控加工的基本原理就是保证切齿过程中刀轴（或砂轮轴）与工件轴在任一瞬时的相对位置与传统加工时相同，运动关系相同。

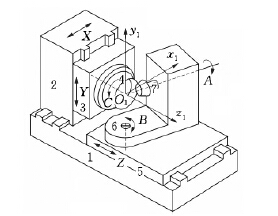
                          图１　ＹＫ２２７５数控铣齿机
      １．床身　２．Ｘ 轴工作台　３．　Ｙ 轴工作台　４．刀盘５．Ｚ 轴工作台　６．工件主轴　７．工件
   
 
      ２．１　含误差的齿面模型
 
 
     基于多体系统理论描述机床拓扑结构，为其各部分编号，如图１所示。令大地编号为０，将铣齿机系统分为两个分支：① 床身、Ｘ 轴工作台、Ｙ 轴工作台、刀盘，铣齿刀；② 床身、Ｚ 轴工作台、工件主轴、工件。

     依据ＹＫ２２７５型螺旋锥齿轮铣齿机各个部件之间的运动关系，建立包含机床几何误差的相邻体变换矩阵如下。

     （１）刀盘与Ｙ 轴工作台之间变换矩阵为

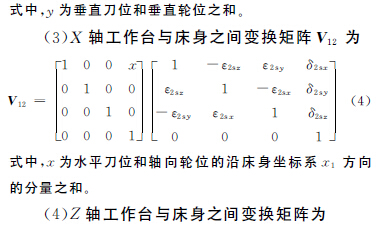
    （６）Ａ 轴工作台与Ｂ 轴工作台之间变换矩阵为

     ２．２　齿面离散
 

     在工程实际测量中，通常沿齿宽方向取９排齿面点，每排取５个数据点，在齿面上均匀地取４５个点，建立全齿面的离散曲面［８?９］，如图２所示。本文的齿面离散方法正是基于这种思想，以已建立的齿面模型为基础，在齿面上选取ｍ×ｎ个网格点作为数字化齿面。具体做法为：将理论齿面向过齿轮轴线的某一平面旋转投影，形成拓扑平面；在该

                
 
                           图２　离散齿面
 

     拓扑平面上取齿宽和齿高方向分别为Ｘ 轴和Ｙ轴，其上任一点对应齿面点的法向误差值为该点的Ｚ坐标值，形成新曲面。新曲面上点的位置按照下式进行计算：

  
     ２．３　映射函数推导
 
 
     各轴误差依据拉丁超立方抽样法［１０］ 进行模拟，抽样区间为［－０．０１，０．０１］，平移量单位为ｍｍ，旋转量单位为（°）。每项误差拟合样本数为１０，且在区间内均匀分布。抽样过程可分为单轴误差影响分析和综合误差分析两步进行。各轴位置误差与运动误差对齿面误差的映射关系记为影响系数ＭＧ：

     依据拟合样本计算齿面各点齿形偏差，选用一阶、二阶或更高阶次回归方程进行数据拟合 。经过拟合结果分析对比，一阶模型预测效果较差，三阶模型预测误差比二阶模型稍大。所以，本文选用二阶模型公式

     作为映射函数，描述几何误差综合作用对齿形造成的影响。
 
 
     ２．４　误差补偿算法
 
 
     在大轮加工过程中，Ｘ轴、Ｙ 轴、Ｚ轴的运动始终描述刀盘原点相对于工件原点的位置矢量。Ｂ轴保持固定角度，保证切削出根锥角。Ａ 轴按照摇台滚轮的滚比关系做轮坯回转运动，此外，在一个齿加工完成后，做分度运动。数控加工模型如下：
 
 
     

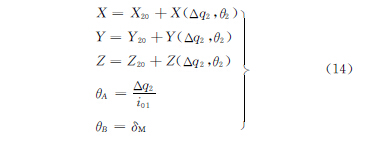
     其中，Ｘ轴、Ｙ 轴、Ｚ轴运动的第一项均为机床基本参数调整的常数项，与机床结构与被加工齿轮具
 
  
     

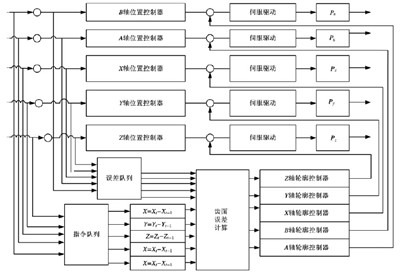
     误差，分析整理出齿面误差变化曲线图。随后，将误差变化曲线作为补偿模型输入，计算数控机构中Ｘ、Ｙ、Ｚ、Ａ、Ｂ 轴动态运动修正值，并将其作为补偿模型的输出，实现对整个加工过程中齿面误差的补偿。
 
 
     图３为控制系统结构框图。

     
  
  
      ３　仿真实验与结果分析

      轮的动态加工过程。参照表１中齿轮副几何参数、机床调整参数，建立的理论齿面如图４ａ所示，采用离散齿面的形式；随机选取第５齿作为研究对象，由不同机床几
何误差生成不同的误差齿面，如图４ｂ～图４ｄ所示，分别为Ｙ 轴直线运动误差引起的误差齿面、Ａ轴回转运动误差引起的误差齿面以及Ｂ 轴定位误差引起的误差齿面。

                         表１　齿轮几何参数与机床调整参数

       
 
                            图４　理论齿面与误差齿面

 
　    依据国家标准ＧＢ／Ｔ１１３６５－８９，选取单周节偏差描述齿面加工精度。如图５所示，其定义为分度圆上，实际齿廓上一点的位置与相邻齿同侧齿廓点的位置之间的距离与理论值间的距离的差。计算公式如下：

                           图５　齿形偏差定义
 

     式中，ｄＴ为公差直径，即中点锥距处与工作齿高中点相交处的直径；ｍ 为中点法向模数，即在中点锥距处法平面上节圆直径与齿数的比值；ｂ为精度等级。
 
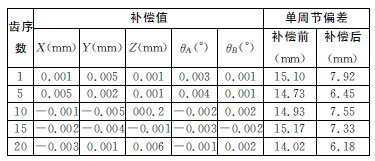
　 　表２显示了实时补偿值与补偿后的齿面单周节偏差。按照式（１７）计算可知，补偿前，齿面精度为６级，补偿后齿面精度达到４级。仿真结果证明，采用螺旋锥齿轮加工误差补偿策略，可以明显提高螺旋锥齿轮五轴联动数控系统的加工精度。
 
 
                             表２　机床参数动态调整示例

     ４　结论
 
 
   （１）依据机床精度与齿面加工质量间的映射关系数学模型，建立两级数控加工误差补偿模型，对加工过程不确定因素对齿面造成的加工质量误差进行了有益补偿，实现了齿面轮廓补偿控制，提高了齿面各点位置精度，能够使产品更好地满足齿轮设计精度要求。
 
 
     （２）利用非线性最小二乘优化方法求解齿面上各点误差最小以及该时刻机床各轴运动修正量最优解。该方法能够准确有效地将齿面误差补偿分解到各轴运动补偿中。
 
 
     （３）为提高模型的准确性，可重复加工过程，对加工出的齿轮齿面误差进行统计分析计算，建立误差范围与修正值的关系。另外，将建立运动轴变化与齿面接触区变化的关系模型，实现对接触区的动态修正。