某型精密数控机床床身的优化设计及性能分析
2021-6-29 来源: 沈机集团昆明机床股份有限公司 作者:张伟华,赛云祥,李佳,黄汉辉
摘要: 以某精密数控机床床身为研究对象,利用有限元技术分析其静动态特性,锁定结构薄弱环节,以此为基础,通过灵敏度法分析床身壁厚、筋板高度及厚度结构尺寸对床身动态特性的影响,并研究了床身内部筋板布局形式变化对床身动态特性的影响,最终给出该型机床整体床身的优选方案。
关键词: 精密数控机床; 床身; 优化设计; 有限元分析; 静动态性能分析; 灵敏度
近年来,随着航空、航天、汽车等行业的发展,对机床的回转速度、进给速度、加工效率、加工精度、性能稳定性、可靠性等方面都提出较高的要求。精密数控机床广泛应用于汽车、航空、航天、船舶、交通、能源、军工等行业中大型箱体类、盘类等精密零部件的机械加工。为了使产品能够适应市场需要,提高市场竞争力,公司开展某精密数控机床系列产品的关键技术研究及其工程应用,围绕某系列精密数控机床的静动态性能、精度、热特性、稳定性及可靠性等方面开展研究。
1、 概述
某精密数控机床作为高速切削机床,必须具有较高的进给速度和加速度,并在高速下仍有高的定位精度。在产品的设计中,其中的大件结构设计( 包括床身、主轴、立柱、工作台、横梁等尺寸和质量较大的零件或部件) ,虽然件数不多,但质量却占机床总质量的 80% ~ 85%。它们不仅是机床的运动支承件,而且是机床外观的主要体现。机床的其它零部件,或者固定在大件上,或者工作时在大件的导轨上运动,因此,大件结构的材料与制造工艺费用在设计中必须加以考虑。对机床进行优化设计的目的就是要使之在满足结构性能的基础上,具有合理的结构布局和最轻的质量,文中仅以床身进行说明。此外,机床结构的动态性能的优劣直接影响机床的工作性能和产品质量,决定着机床的加工精度。所以研究机床动力学特性对加工性能和加工精度的影响规律找到解决工程应用中出现的机床振动、精度不稳定等问题,提升机床的整体性能,为高性能机床的产业化铺平道路。某精密数控机床,如图 1 所示。其床身设计是其重难点之一,因为它承载机床绝大部分的部件和载荷,其刚度、固有频率等直接影响整机的加工性能和效率,因此对床身进行优化设计及性能分析具有重要意义。

图 1 精密数控机床整体布局
2、床身结构方案模型优化及性能分析的目的
确定床身载荷及约束条件后,建立床身的有限元模型,建立合理的结构单元、网格大小。通过载荷添加及边界条件约束后,进行求解计算,通过拓扑优化,获取结构载荷传递路径,确定结构的概念造型,通过拓扑结构圆整,获取床身的结构三维模型,对模型进行性能分析。通过对结构特征进行参数建模,并在有限元分析软件中进行分析和优化,确定结构特征的灵敏度,确定结构特征的较优结构尺寸,最终获得床身静动态性能较优的结构模型。其优化的数学模型为:

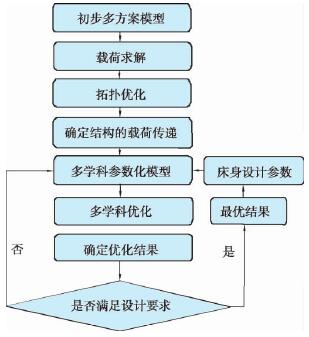
图 2 结构方案优化确定
床身性能分析及优化工作的主要内容和目的: ( 1) 确定载荷传递路线及主要结构特征。( 2) 考察床身在静态载荷条件下的变形特性,对其静刚度进行校核和验证。( 3) 考察主要结构件固有的动态特性,分析其动态薄弱环节,为整机动态分析设计提供依据。( 4) 对不同的设计方案进行分析、比较和优选,进行床身的轻量化设计。
3、床身结构方案的优化及性能分析
3. 1 床身结构拓扑优化
以减小的材料质量为状态变量,对床身的原始模型进行形状拓扑优化计算,为后期的详细设计提供依据,目的是确保其承载能力的基础上减轻床身质量,降低制造成本首先,根据工艺需求分析,确定床身结构尺寸参数和初步结构方案,并对结构方案进行拓扑优化,确定床身结构的载荷传递路径。如图 3 所示,根据设计任务书要求,床身结构确定为 T 字形整体式床身。建立床身三维结构骨架模型,对床身进行有限元划分,并对床身地脚螺栓支撑进行约束,如图 4所示,导轨上承受 20 000 N 工作台的载荷,30 000 N最大加工工件载荷,再加上立柱滑板主轴箱载荷,其前处理如图 5所示,床身材料弹性模量为 1. 5× 10(11次方)Pa,泊松比为 0. 25,密度为 7400 kg /m(3次方) 。
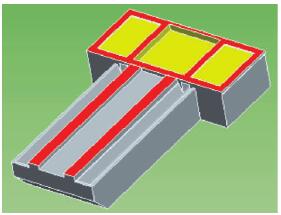
图 3 床身结构初步方案图

图 4 床身地脚螺栓
以机床质量和体积因素为设计变量,以床身变形最小、1 阶固频最大为约束条件,以质量降低为设计目标,对床身进行拓扑优化,其优化结果如图 6 所示。通过对结构进行拓扑优化,确定载荷的传递路径及床身结构的主要支撑着力点。
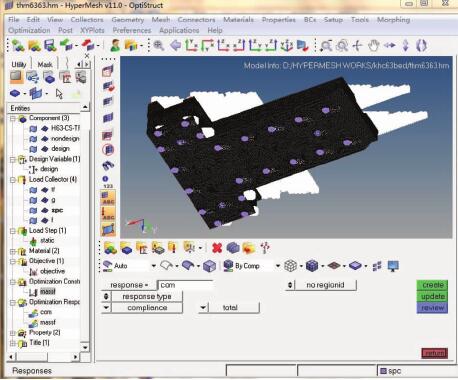
图 5 拓扑优化前处理
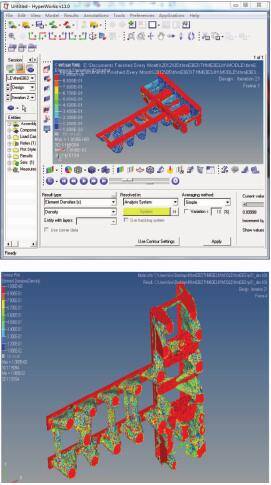
图 6 整体式床身的拓扑优化结果
3. 2 床身的建模分析及优化
对拓扑优化后的结构进行结构圆整,确定床身结构筋板主要布置形式,并通过参数化建模软件,建立床身结构三维参数化模型。如图 7 所示。

图 7 整体床身结构的参数化模型
建立床身结构的有限元模型,对床身结构进行静、动态分析,主要是: ( 1) 考察结构在静态载荷条件下的变形特性,对其静刚度进行校核和验证。( 2) 考察结构固有的动态特性,分析其动态薄弱环节,为整机动态分析设计提供依据。
3. 2. 1 不加工件,只考虑工作台重力和床身自重
通过对床身的静力学分析,床身的整体变形如图 8 所示。分析结果显示: 床身最大变形约为 8. 2 μm,导轨上的变形为2~5. 6 μm,其中最大变形为 5. 6 μm 出现在 Z 轴方向2. 15 m处( 床身后面为零点) 。
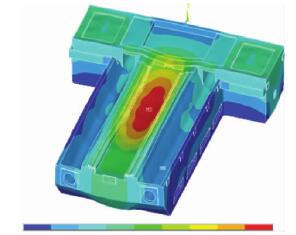
图 8 不加工件,床身静载变形图
3. 2. 2 考虑实际工况载荷
以一种典型工况为例: 工件和滑块总质量为 5 t,作用在上导轨上; X 向的切削力为 6 600 N; 立柱自重为 10 t,并考虑床身自重。变形情况如图 9 所示。结果显示,此时最大变形约为16 μm;主要考虑导轨上的变形,其变形为 5 ~ 12. 4 μm; 其中最大变形12. 4 μm 仍出现在 Z 轴方向 2. 15 m 处( 床身后面为零点) 。
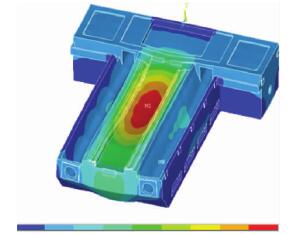
图 9 考虑实际工况下床身静载变形图
3. 3 模态分析
在床身底面施加位移约束,计算所得前 5 阶模态频率与振型如表 1 所示。
表 1 床身前 5 阶模态频率与振型
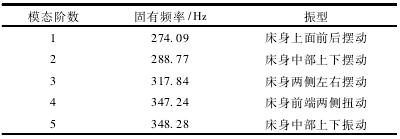
图 10 给出了床身的前 3 阶模态振型图。其中第 1 阶振型为床身上表面的前后摆动; 第 2 阶振型为床身中部的上下摆动;第 3 阶振型为床身两侧的扭动。
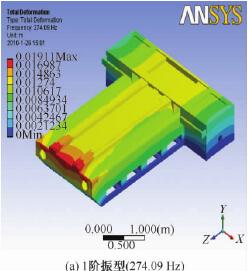
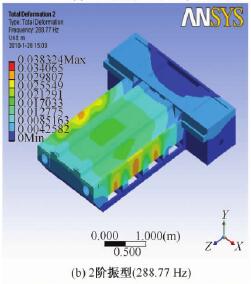
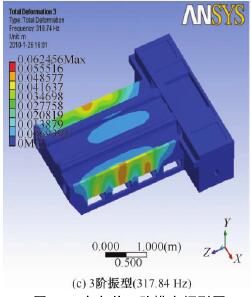
图 10 床身前 3 阶模态振型图
由以上分析可以看出床身固有频率比较高,考虑到主激励源频率大约在 50 Hz 左右( 工作转速在 3 000 r/min) ,故床身满足整机总体动态特性要求。4 床身导轨及内部筋板的优化。
4. 1 前部床身导轨优化
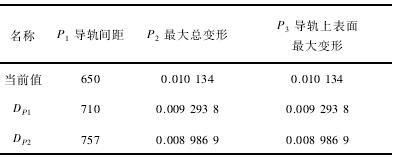
其中: P1为前部床身两根导轨的间距,P2为最大总变形,P3为导轨上表面最大变形。DP1点为宽度增加 60 mm 后,Dp2为宽度增加 107 mm 后结果。原模型为 650 mm,增加 107 mm 后,其最大变形为 8. 9 μm,变形减少 1. 1 μm。如表 2 所示。
表 2 导轨优化后变形 mm
4. 2 前部床身筋板厚度、高度参数优化
对筋板布置进行参数优化,通过改变筋板参数数值,进行计算分析,获取筋板参数对床身变形的灵敏度图,从而取得较优的筋板结构参数,其优化形状及参数如图 11 ~ 图 14所示。

图 11 床身竖筋
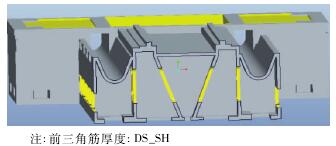
图 12 床身三角筋
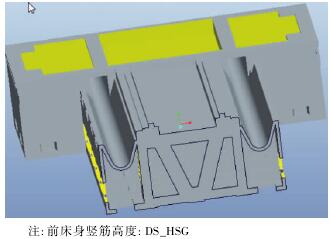
图 13 床身竖筋高度
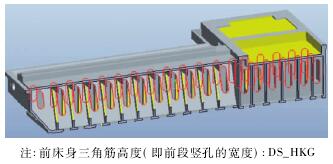
图 14 床身三角筋高度
( 1) 采用表 2 中第 3 组结果 C 时,导轨最大总变形减小0. 6 μm,总质量减小 200 kg。此时 4 个参数分别为: 筋板厚度:DS_LH 为 12.51 mm ( 减小 8 mm) 、DS _SH 为 34.85 mm ( 增加4 mm) 、高度 DS_HSG 为 107. 7 mm( 增加 17 mm) ; DS_HKG 为80 mm( 减小 20 mm) 。如表 3 所示。
表 3 筋板参数优化结果
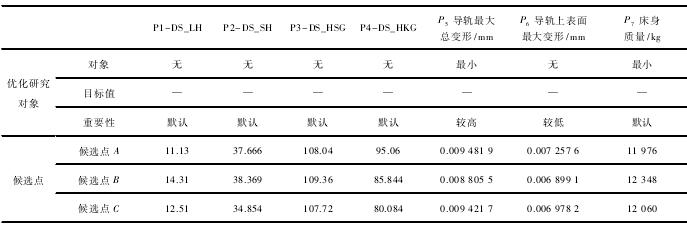
( 2) 各参数的灵敏度。
文中以床身的壁厚、筋板高度及筋板厚度作为一组设计变量,利用灵敏度法分析各结构参数变化对床身动态性能的影响。结果如图 15 所示。
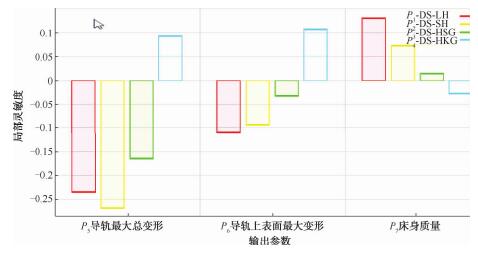
图 15 床身各参数灵敏度
( 3) 最终床身优化结构。
①床身导轨变形较大,达到 10 μm。为减小变形,对床身筋板厚度、筋板高度进行优化,优化后变形为 8 μm,变形减少 20%。
②前部床身整体结构较差,仅对筋板厚度、高度进行优化变形减小有限。由于前部床身中间没有支撑( 仅靠前部两点) ,且导轨靠近前部床身中间,故变形较大。通过不断优化,导轨间距离增加 125 mm 后,变形减小 1. 2 μm,变形减少 12%。其最终结果如图 16 所示。
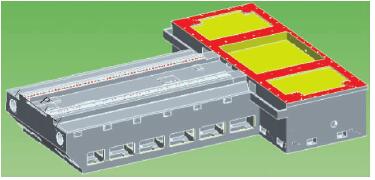
图 16 整体式床身的最终三维结构
经过多次分析计算和相应的结构优化,床身结构的各项性能指标均达到了设计目标值,取得了较好效果。
5、结论
通过有限元模型确定结构方案,再对结构方案进 行拓优化,静、动态模态分析; 找出床身结构的薄弱点,并不断优化导轨及内部筋板的结构,达到最终的最优结构。采用该方法,可获得床身在不同载荷工况下承受的载荷大小,从而为精确计算不同工况下导轨变形提供准确载荷模型。可以快速获取结构件在不同工作位置及受力工况下静动态性能,并通过结构参数化设计可以获取不同方案下结构的综合性能,从而能够快速确定较佳的结构方案。推广并运用在机床其他大件的优化设上,取得了良好的效果。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息





