基于刀具失效率的换刀策略研究
2016-12-27 来源:东北大学机械工程与自动化学院 作者:王新刚 吕春梅1 赵玉倩 陈晓明
摘要:将影响机加工艺可靠性的主要因素刀具的失效率作为研究对象,将刀具的切削参数作为随机变量,以最大似然估计为基础,结合可靠性分析方法,建立机加工艺系统的动态可靠性数学模型,推导各工序刀具的失效率计算公式。在此基础上,以刀具失效率为判据,建立了如何确定被更换刀具的工序及换刀时间的方法。研究结果表明,当整体工艺流程系统可靠度低于某一阈值时,即可确定更换刀具的时间,再应用刀具失效率模型,就能够迅速找出失效率最大的工序所使用的刀具,并及时更换,从而确保刀具在失效之前满足工艺可靠性要求,最大限度地利用刀具,减少换刀次数,降低成本,从而保障整体工艺系统的高可靠性。
关键词:机械制造工艺与设备;动态可靠性;失效率;刀具
0. 引言
在高精自动化技术得到广泛应用的今天,机械行业对产品整个工艺流程的可靠性提出了更高的要求,它与机床、刀具、操作者的可靠性息息相关。其中刀具的可靠性是最重要的影响因素,所以研究刀具的可靠性及失效率显得至关重要。如果刀具可靠性差、失效率高,就会造成换刀频繁,产品不合格率上升,消耗更多的工时和经济成本。
Ramalingam等?对刀具的可靠性进行了研究,建立了确定刀具耐用度的概率模型。文献[2—3]提出了一种基于简单的调度规则和通用搜索的启发式模型。Oral等H o定义了可用于回转零件工艺设计系统的计算机辅助优化方案,它规定一个最佳方案必须具有最少的换刀次数和最短的刀具空行程时间。Rodriguez等¨1提出了最佳换刀时间的数学模型,降低了对工艺可靠性的影响。李兆前等¨o对刀具可靠寿命进行了深入的理论研究和实验研究,建立了相应的可靠性数学模型。陈雪峰等¨1、王新刚等¨1通过实验数据分析和理论分析建立了几种刀具可靠度数学模型,同时进行了大量的可靠寿命切削试验来保证刀具的高可靠性。上述国内外学者大都研究如何进行合理地机械调度与规划以达到减少工时的目的,或者单一对刀具进行可靠性及寿命分析,并没有分析每道工艺所使用刀具的可靠性对整体机加工艺可靠性的影响。除此之外,在传统的刀具可靠性模型中,一般认为刀具的切削参数一旦选取在整道工序中将保持不变。而实际生产情况表明,在连续切削加工过程中,即使同一台机床,由于机械振动、加工材料的质地分布情况等因素的影响,它的切削参数也是随机变化的一一0|。在这种情况下应如何保证总体工艺流程的可靠度、在何时换刀、该更换哪道工序的刀具,对这类问题的研究还未见报道。
本文结合工艺流程设计、可靠性和动力学的知识,在刀具的切削参数作为随机变量的前提下,推导刀具可靠度和失效率的计算公式,并建立基于刀具失效率的整体机加工艺流程可靠性的数学模型。该模型能够准确地确定需要被更换刀具及换刀时间,进而为减少工时与成本,同时保证产品质量及提高产品合格率提供理论依据。
1. 工艺流程动态可靠性模型的建立
一个完整工艺流程的可靠性与每一道工序的可靠性密切相关,而每一道工序的可靠性又受到机床、操作者以及刀具可靠性的影响。机床的可靠度由其本身的结构以及设计决定,包括自动化程度、所处工作环境、也与工厂管理者所制定的维护方案有关,常采用经验值,某一台机床的可靠度可由建立在实验基础上的“无故障时间数据库”取得。操作者的可靠度也可通过实验获得。本文中主要研究刀具的可靠度,而机床和操作者本身的可靠度认为是不变的。在加工零件时,机床、操作者、刀具组成一个串联系统且相互独立,则整个工艺流程的可靠度可表示为

刀具的可靠度依赖于机床的实际工作情况,且与各切削参数有关。通常刀具的可靠寿命服从指数分布,本文研究的换刀策略并不只限于刀具寿命服从指数分布,也可以服从任意分布。文中以服从指数分布为例来说明实施该策略的具体步骤,则有一道工序时的可靠度。


2.刀具失效率模型的建立
实际生产加工过程中,一个完整的工艺流程包括多道工序。假设不同的工序使用不同的刀具,当整个工艺流程的可靠度R。(Ⅳ)低于许用的可靠度值时,必须换刀,在达到目标产量之前可能需要进行多次换刀。如果不换刀,会导致整体工艺流程可靠度的降低、产生废品和增加经济成本。由于涉及不同的工序及刀具,如何选择需要被更换的刀具成为关键性的问题。本文采用计算各工序刀具失效率的方法来确定需要被更换的刀具,刀具失效率最大的最先更换。每次换刀前后整个工艺流程的可靠度变化趋势如图1所示。
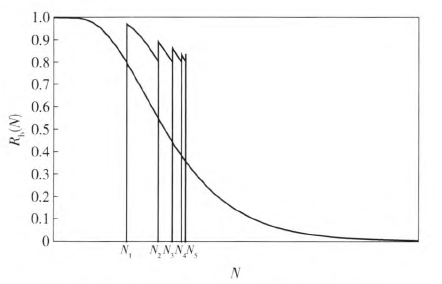
图l 每次换刀前后整体工艺流程司靠度的变化趋势
图1中的Ⅳ。、Ⅳ:、Ⅳ3、Ⅳ4是换刀时加工零件的个数。假设工艺流程整体可靠度不能低于0.8这个阈值,那么在Ⅳ.点换刀时,整体工艺流程的可靠度由原来0.8的位置提升到大致0.97的位置;在Ⅳ:点换刀时,整体工艺流程的可靠度由原来0.82的位置提升到大致0.95的位置。第2次换刀之所以在整体工艺流程的可靠度高于0.8阈值,是因为再继续加工出一个零部件后整体工艺流程可靠度将要低于0.8,这样就会出现废品或者停车事故,所以需要提前一个零部件进行更换。从图1中可以看出,通过及时确定被更换的刀具和更换时间就能够始终保持整体工艺流程的可靠度高于阈值。
由(5)式给出整个工艺流程的可靠度公式可知,当整个工艺流程可靠度低于许用值时,更换刀具的时间就确定了。这时就需要计算各工序刀具的失效率,为确定更换刀具提供理论依据。已知刀具的失效率函数为
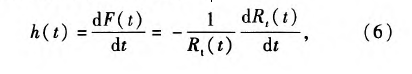

当更换刀具的时间确定后,由(7)式计算各工序刀具的失效率,失效率最大刀具的最先替换掉。若替换之后整体工艺流程可靠度仍小于阈值,就需要替换此时失效率最大的刀具,直至整体工艺流程可靠度仍大于阈值为止。一次换刀有可能更换一把,也有可能更换多把。
3.工艺流程换刀时间
从厚度为34 mm的Q235钢板中切下90 mm×90 mm的钢板,通过铣削、钻削、铰等加工工艺使其满足尺寸、形状、公差等要求。图2和表1分别给出了零件具体形状和具体要求。
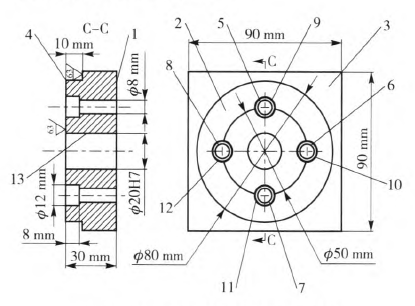
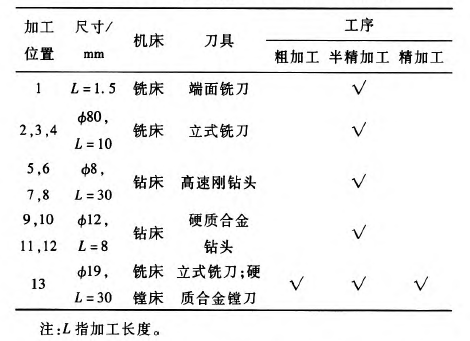
表1 盘类零件各部分加S-要求
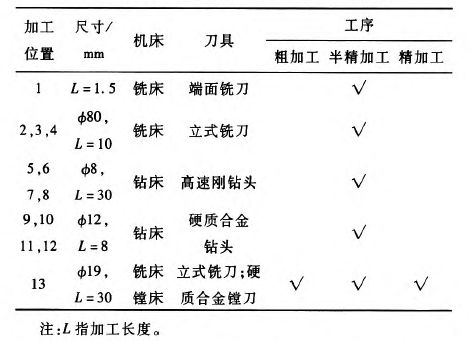
图2中,将零件分为13个部分,每部分根据可图2中,加工表面的不同特征使用不同的工序,进而确定各工序的先后顺序。这里,假设操作人员不会出现失误,刀具的各切削参数都是随机变量,且服从任意分布‘12 3(本文以变量均服从正态分布为例)。各道工序及相应的加工时间,均可通过Mastercam仿真得到。在Mastercam中选择正确的加工工艺,输入相应的预先选取好的参数,进行仿真,查看工序时间并记录,具体结果见表2.
表2 盘类零件各工序
利用表2中的参数构造最大似然函数,求得各工序参数 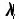 、a、 β1、 β2 、β3 ,结果如表3所示。
、a、 β1、 β2 、β3 ,结果如表3所示。
表3 各工序的参数值
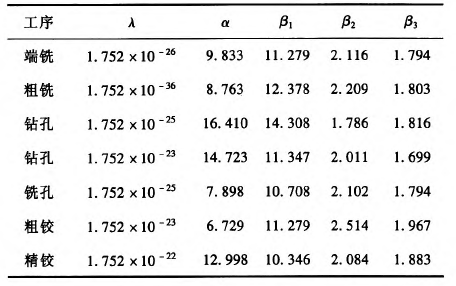
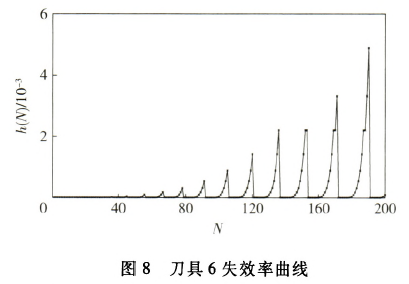
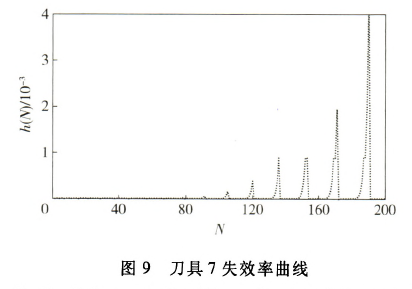
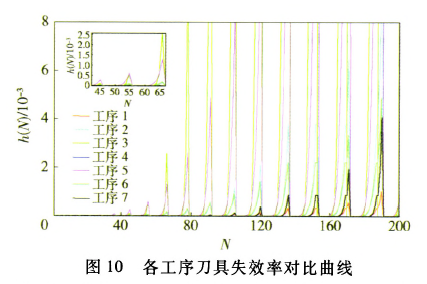
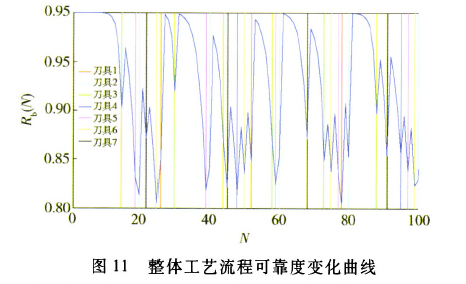
各工序可靠度可由(4)式计算获得,其中各工序工时及切削参数由表3获得,最终可根据(5)式计算出整个工艺流程的可靠度。这里,假设整体工艺流程许用可靠度为0.8.若可靠度小于0.8,则必须进行换刀。此时通过(7)式计算出各刀具的失效率并进行比较,确定更换刀具的工序与时间。图3~图9为各工序刀具的失效率随加工零件个数的变化曲线。从图10中各工序刀具失效率对比曲线可以看出,在加工一定数量工件时第几道工序的刀具失效率最大,为更换刀具提供判据。图11为换刀前后整个工艺流程的可靠度随加工零件个数的变化曲线。从图11中可以看出,当加工第18个零件时,计算得到整个工艺流程的可靠度
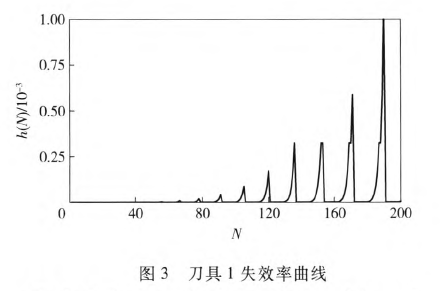
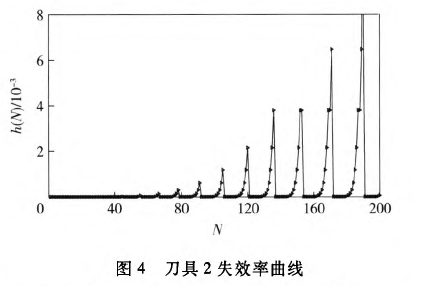
为0.768 4,小于许用值0.8.这表明加工第17个零件就需要进行换刀,这是整个工艺流程的第一次换刀。但具体更换哪个工序的刀具还需要结合图10确定。当加工第18个零件时,工序5中对应的铣刀失效率最大,必须将它换掉。换刀之后,重新计算整
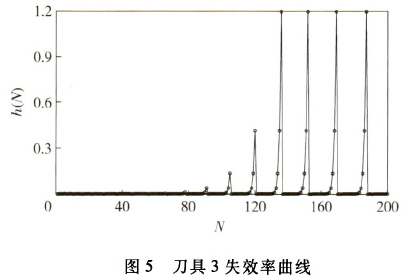
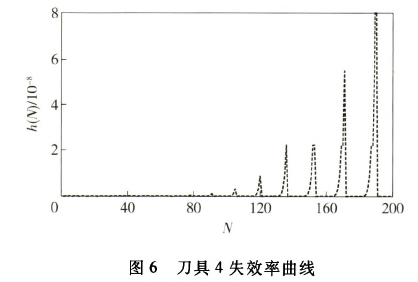
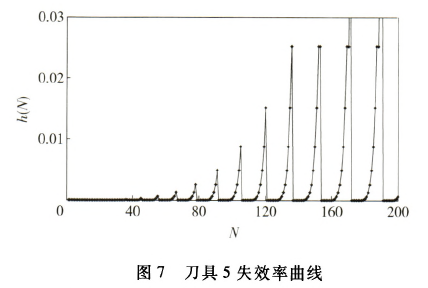
体工艺流程的可靠度值为0.998 4,这时提高了整个工艺流程的可靠度,各工序及刀具可继续切削加工,直到整体工艺流程可靠度再次小于许用值0.8时,再次进行换刀,直至完成所有需要加工的零件。
4. 结论
I)建立了整体工艺流程系统的可靠性数学模型,通过该模型可以判断出需要换刀具的时间点。2)建立了刀具失效率数学模型。通过该模型能够迅速判断需要换刀工序及刀具,确保刀具在
破损或磨损失效之前还能满足工艺可靠性要求。3)提出了基于灵敏度的换刀时间和工艺动态可靠性研究方法。通过改变即将失效刀具所对应的敏感参数的数值来提高刀具和整体工艺流程的可靠度,从而达到了延迟换刀、降低成本的目的。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com





