摘要: 基于有限元法参数化建立主轴系统三维有限元模型,将轴承简化为弹性支撑. 考虑皮带轮和卡盘的影响,对整个主轴系统进行模态分析,得到主轴系统的前八阶固有频率及固有振型. 进行临界转速分析,将工作转速与非零最低阶频率对应的转速进行比较,验证主轴设计的合理性. 利用ISIGHT 集成ANSYS 进行正交试验设计并计算非零最低阶固有频率,将有公差范围要求的轴段的直径和长度以及基本物理参数作为随机变量,采用BP 神经网络拟合主轴系统非零最低阶固有频率与随机变量之间的关系. 利用一次二阶矩法计算主轴系统在特定转速下的可靠度并求解各随机参数的可靠性灵敏度.
关键词: 主轴系统; 有限元法; 神经网络; 可靠度; 可靠性灵敏度
主轴系统是数控车床的关键部件[1 - 4]. 主轴系统的动态特性很大程度上决定了整个机床的加工质量和切削稳定性. 主轴系统工作频率接近其固有频率时会发生共振,从而严重影响车床的加工精度. 因此,主轴的正常转速必须远离其临界转速.
在设计加工过程中,主轴系统不同轴段的尺寸会有一定偏差,将其视为影响主轴系统可靠度的随机变量; 尺寸的微小变化会引起整个主轴系统固有频率的变化. 由于各随机变量的影响程度不同,因此研究频率可靠性及主轴系统失效概率对各随机变量的灵敏度具有重要的意义.
本文基于有限元软件[5]对数控车床主轴系统进行参数化建模,利用ISIGHT[6]集成ANSYS进行正交试验设计,对随机参数进行抽样,计算非零最低阶固有频率. 根据抽样计算结果,结合BP神经网络技术得到了主轴系统非零最低阶固有频率与所有随机变量的拟合关系,进而利用一次二阶矩法计算主轴系统在最高转速时的可靠度并求解可靠性灵敏度.
根据主轴系统有限元分析结果以及可靠性灵敏度计算结果,指导实际设计加工.
1 、主轴系统有限元模型
1. 1 主轴系统基本结构及参数
主轴是一种典型的中空阶梯轴,将锥度较小的轴面简化为等直径轴面,将轴内孔径视为常数,忽略轴段倒角及圆角. 主轴前端安装标准三爪卡盘,末端固联皮带轮. 在主轴高速旋转过程中,可将皮带轮和卡盘与主轴视为一体,经合理简化后的主轴系统结构如图1 所示.
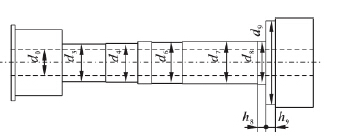
图1 主轴系统结构简图
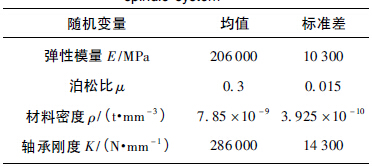
主轴系统的基本物理参数如表1 所示. 图1中标注出的各轴段直径、主轴内孔直径以及后两轴段长度均有尺寸范围要求,因此作为尺寸随机参数. 将弹性模量、泊松比、轴承刚度、材料密度这4 个物理参数同样看作随机变量. 所有随机参数均服从正态分布,标准差取为均值的5%.
表1 主轴系统基本物理参数
1. 2 轴承的简化及约束
本文将前后轴承均简化为弹性支撑,支点位置位于轴的表面,如图2 所示. 在主轴的前、后端分别有轴承支撑,因此需要建立8 个弹簧单元. 假设轴承只具有径向刚度,且刚度值为常数,见表1.
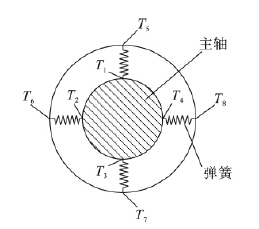
图2 轴承弹性支撑示意图
根据轴承特点及主轴系统结构,对弹簧施加约束时,约束其自由端的全部自由度,即对图2 中的T5,T6,T7和T8点进行完全约束. 对于弹簧与轴表面的接触端,在前轴承处施加轴向约束,后轴承处不约束,对应图2 中的T1,T2,T3和T4点.
1. 3 主轴系统有限元模型
使用8 节点SOLID185 单元和COMBIN14 单元分别建立主轴和弹簧单元. 对主轴系统进行适当简化,按照有限元分析的要求,使弹簧约束处节点号固定不变,将主轴系统划分为6 976 个单元,8 928 个节点,有限元模型如图3 所示.

图3 主轴系统有限元模型
2 、主轴系统模态分析
主轴系统的静力分析[7]体现刚度对主轴加工精度的影响. 模态分析通过研究无阻尼系统的自由振动,得到其自然属性. 进行模态分析可以直观地了解主轴系统的固有频率及变形程度[8].
首先根据达朗贝尔原理,建立动力学基本方程:
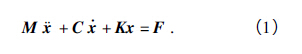
式中: M,C,K 分别为质量、阻尼和刚度矩阵; x,x·和x··分别为位移、速度和加速度矩阵; F 为激振力矩阵.对于本文来说,进行模态分析是研究主轴系统无阻尼自由振动特性,从而得到其固有频率和振型; 因此忽略阻尼矩阵影响,且自由振动时无外界激振力,即阻尼矩阵C 和激振力矩阵F 均为零矩阵. 设解为
![]()
将式( 2) 代入式( 1) ,并使特征矩阵行列式为零,得到关于ω 的n 次方程,开方后得到n 阶固有频率.
根据第1 节中对数控车床主轴系统的参数化建模,进行模态扩展和结果后处理,利用有限元软件进行模态分析,使用Block Lanczos 法提取固有频率,选取前8 阶振型,各阶固有频率数值及对应的振型分别如表2 和图4 所示.
表2 主轴系统前8 阶固有频率及振型
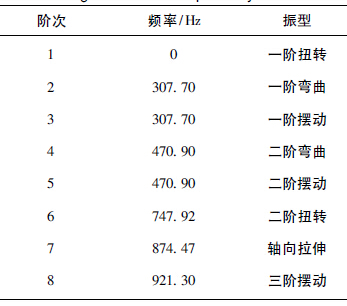
由以上结果可以看出,第1 阶频率为0. 第2,3 阶频率相同,第4,5 阶频率相同,表现为正交;可以将其视为重根,其振型也只是方向不同. 第6阶和第7 阶频率为单根,其振动形式分别为扭转和拉伸,而没有弯曲和摆动. 进一步求解主轴系统的临界转速:n = 60f . ( 3)式中: n 为临界转速,r /min; f 为频率,Hz.根据式( 3) 和表2,计算出各阶次频率对应的转速为: 第1 阶0; 第2,3阶同为18 462 r /min; 第4,5 阶同为28 254 r /min; 第6 阶为44 875. 2 r /min; 第7 阶为52 468. 2 r /min; 第8 阶为55 278 r /min.只考虑转速非零的最低阶即第2,3阶固有频率所对应的转速[9]. 本文中主轴系统的工作转速最高值为6 000 r /min,小于2,3阶固有频率所对应的转速,即18 462 r /min.
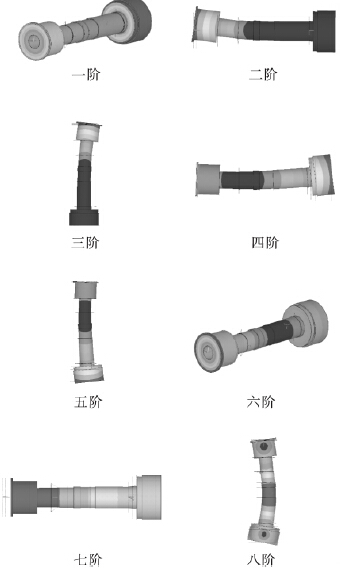
图4 主轴系统前8 阶振型图
3 、ISIGHT 试验设计及神经网络拟合
利用ISIGHT 集成ANSYS 设计正交试验,通过修改模拟计算模块的输入文件来完成对模型的修改,从而能够高效地得到所需数据.
将图1 中标注的9 个尺寸参数及表1 中所列出的4 个基本物理参数共13 个参数作为随机变量,采用拉丁超立方( LHS) 设计方法,得到需要的样本,最后通过ISIGHT 与ANSYS 接口调用ANSYS 进行相应的有限元分析和计算,得到主轴系统非零最低阶固有频率的值.
利用BP 神经网络[10]拟合主轴系统非零最低阶固有频率与设计变量之间的函数关系. 隐含层的激励函数选用Sigmoid 函数,输出层的激励函数选用线性Purelin 函数,则上述函数关系可表示为
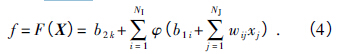


图5 网络训练输出值与有限元分析值的比较
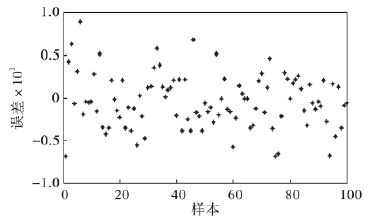
图6 网络训练误差
4 、频率可靠度及可靠性灵敏度计算
研究主轴系统在最高工作转速即6 000 r /min( 对应频率100 Hz) 时的可靠度及可靠性灵敏度.可靠性指标β 是一个无量纲数[11 - 12]:
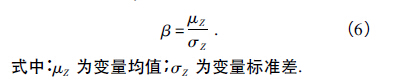
一次二阶矩法将功能函数展开成泰勒级数并取至一次项,按照可靠性指标的定义形成求解方程,只需要变量的均值和方差即可求解.
设功能函数为gX( X) ,将功能函数在均值处展开,得到可靠性指标β 的近似表达式为

式中Φ 为标准正态分布函数.
基于神经网络拟合得到的数学模型,建立功能函数gX( X) = F( X) - 100,这里F( X) 为神经网络的输出值,100 为本文所研究的主轴系统最高转速6 000 r /min 对应的频率即100 Hz. 利用一次二阶矩法得到主轴系统结构的可靠度分析结果. 其中,可靠性指标β = 4. 841 3,频率可靠度R =0. 999 999 355 .
进而求解主轴系统失效概率对各尺寸随机参数的灵敏度. 可靠性灵敏度[13 - 14]就是结构系统基本随机变量的变化引起结构失效概率变化的敏感性. 失效概率对随机变量均值和方差的灵敏度计算表达式分别为
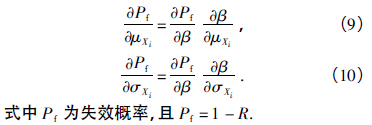
材料参数及轴承刚度在机械加工中通常难以控制,因此本文主要研究前文所述的9 个尺寸参数即X =[d0,d3,d4,d6,d7,d8,d9,h8,h9]对主轴系统可靠性的影响. 可靠性灵敏度计算结果如下:
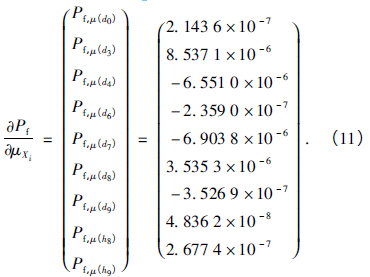

从失效概率对随机参数均值的灵敏度矩阵式( 11) 可以看出,d0,d3,d8,h8,h9数值的增加会导致主轴系统频率稳定性变差; d4,d6,d9数值的增加则导致主轴系统频率的稳定性更好.
从失效概率对随机参数标准差的灵敏度矩阵式( 12) 可以看出,所有随机参数数值的增加可以导致主轴系统频率稳定性变差.
5 、结语
本文基于有限元方法,利用有限元软件对数控车床主轴系统单元进行参数化建模. 利用ANSYS 的模态分析得到主轴系统的前8 阶固有频率及相应振型. 比较主轴系统的工作转速与临界转速,分析进行可靠度计算及灵敏度设计的必要性. 基于ISIGHT 软件进行正交试验设计,利用BP 神经网络拟合出功能函数表达式. 利用一次二阶矩法求解主轴系统的频率可靠度并求解各随机参数对失效概率的可靠性灵敏度,说明了各尺寸参数变化对于该主轴系统频率可靠度的影响程度. 所得数据结果对于指导零部件参数设计、实际生产加工和主轴使用寿命提高具有指导意义.
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com





