螺纹数控修复车床主轴部件动态特性分析(中)
2017-4-7 来源:沈阳工业大学 作者:肖磊
第 3 章 螺纹数控修复车床主轴部件有限元分析
3.1 螺纹数控修复车床主轴部件简介
对主轴部件进行动态特性分析,首先要对主轴建立合理的有限元模型。在对主轴进行有限元建模时要考虑到诸多因素对其动态特性的影响,比如在划分单元、处理结合面问题以及考虑轴承支撑刚度等问题时都要仔细分析,以便最后计算出最接近主轴工作状态下动态特性。因此在对主轴进行动态特性分析时,一定要正确处理好模态分析各种因素对其动态特性的影响,合理设置其影响参数,为下一步进行有限元分析计算打好基础。本章在借鉴以前学者在类似动力学问题分析的基础上,对现有的一款螺纹数控修复车床的主轴系统进行合理的有限元建模。
3.1.1 主轴结构介绍
该数控螺纹修复车床为石油行业的专用机床,主要用来车削修复钻铤、钻杆等钻具。工作时,钻具由送料架从左端输送至主轴内部至右侧卡盘处,再由卡盘卡紧,通过主轴旋转带动工件旋转,由刀具完成切削修复工作。主轴旋转带动工件旋转为机床的主运动,其动态特性直接影响机床的切削精度,所以对该车床主轴部件进行动态特性分析具有重要的现实意义。
该车床主轴部件如图 3.1 所示,主轴后端由背靠背的两个圆锥滚子轴承支撑,前端由一个双列圆柱滚子轴承支撑,轴承靠端盖、箱体和锁紧螺母实现轴向定位,同时箱体内壁设置有轴承润滑系统,轴上齿轮也由两个锁紧螺母实现轴向定位。
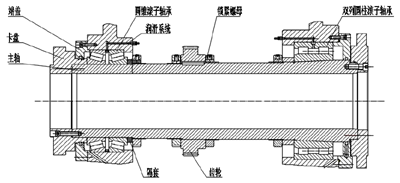
图 3.1 主轴部件结构示意图
3.1.2 主轴模型简化
通过查阅大量相关资料,发现在进行主轴动态特性分析时,一些结构上的细节问题对动态分析结果影响很小,所以为了降低工作量,缩短有限元分析计算的时间,设计人员通常会在主轴进行有限元建模前会对其进行必要的简化,以提高工作效率[33,34],主要体现在以下几个方面:
(1)对于安装在主轴上及内部且不属于主轴本体的传动零件,在进行动态特性分析时只考虑他们的分布质量,将其质量等效附在主轴或主轴架的壁厚上。
(2)忽略对主轴质量影响较小的结构,如主轴上的螺纹孔,键槽及尺寸较小的凸台等,这些结构对主轴的振动特性影响较小,可以忽略不计,在建模时进行必要简化,可以简化网格划分,减少前期准备时间。
(3)去除功能件和非承载件,合理修改和补充截面形状;对非关键部位的孔、退刀槽及台阶等尽量简化,对截面特性影响较小的结构适当忽略。
(4)简化主轴上的节点,对距离很近的两个节点可视为一个节点处理,对于靠的很近并且结构和功能相同的构件等效成一个构件。
(5)对支撑主轴的轴承进行简化处理,忽略轴承的角刚度,只考虑其径向刚度,即将轴承简化为只提供径向支撑力并可压缩的弹簧。
(6)材料本身特性具有线性和非线性,各向同性和各向异性等差别,在对机械结构进行模态分析时,通常只考虑结构材料属性中的线性特征,必须对结构材料的弹性模量 EX 和密度 DENS 等进行设定,忽略其属性中的非线性特征对机械结构动态特性的影响。
本文在充分考虑上述条件后,对该车床主轴部件进行了适当的简化。忽略了主轴两端的螺纹孔;对尺寸变化较小的部分轴段进行了统一尺寸;忽略了主轴连接齿轮部分的键槽;忽略了主轴两端及各轴肩处的倒角等。图 3.2 即为简化处理后的主轴结构简图。
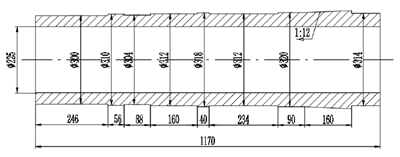
图 3.2 简化后的主轴结构
3.2 主轴的有限元模型
3.2.1 主轴有限元建模方法
对主轴进行有限元建模属于有限元分析的前处理部分,也是机械结构有限元模态分析最重要的一环,能否合理建立模型对后续分析计算的准确性和计算成本产生直接影响[35]。目前对主轴进行有限元建模主要有两种方式,一种是通过有限元软件直接建模,另一种是利用其它三维实体建模软件对主轴进行建模,再通过数据转换将建好的实体模型转换到有限元分析软件中,建立有限元模型。两种方法各有优缺点,设计人员可根据实际情况进行选择。
在有限元软件中有两种建模方法:自顶向下与自底向上。自顶向下进行有限元建模时,首先需要设定一个最高级图元,如棱柱、四方体、球体等,用户可通过布尔运算进行图元的相互数学运算,得到所要建立的有限元模型。自底向上进行有限元建模时,首先在最低级的图元上构造模型,如关键点,线,面等,通过相应的拉伸、旋转等过程,最终建立结构的有限元模型。而通过其他三维实体建模软件建模再利用数据转换导入到有限元分析软件进行结构的有限元建模相对简单些,可以节省设计时间。本文数控螺纹修复车床的主轴为简单的阶梯轴,截面形状较为简单,采用第二种建模方法进行有限元建模。
首先利用二维制图软件绘制主轴的截面图,并将其导入三维建模软件中旋转即得到了主轴的三维实体模型,保存成.prt 格式文件,即可将其导入有限元分析软件中,进行网格划分,建立的主轴模型如图 3.3 所示。

图 3.3 主轴模型
3.2.2 单元选择和材料设置
通过前面的介绍分析,主轴结构较为复杂,对于本课题所研究的阶梯中空主轴应采用三维实体单元对其进行模拟分析。有限元软件提供常用的三维实体单元有SOLID45、SOLID46、SOLID64、SOLID87、SOLID90、SOLID95 等,本文主要研究主轴系统自身在装配条件下模态参数的变化情况,选取 SOLID45 单元进行模拟分析,用于三维实体结构模型,如图 3.4 所示。
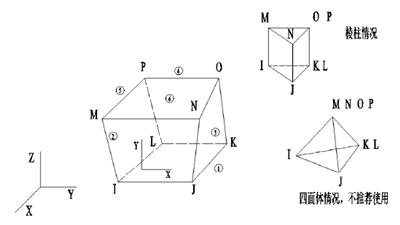
图 3.4 SOLID45 单元的几何形状
SOLID45 单元是由 8 个节点在空间结合而成,每个节点有 X、Y、Z 三个方向的自由度。该单元具有塑性、蠕变、膨胀、应力强化、大变形和大应变的等特征,通过其可以获得简化的综合微控选项。表 3.1 为 SOLID45 单元的输入参数。 表 3.1 SOLID45 单元的输入参数
表 3.2 结构材料的属性参数
3.2.3 网格划分
有限元软件提供了多种网格划分方式,如 Sweep 网格划分、Tetrahedrons 网格划分、Automatic 网格划分和 Multi Zone 网格划分等方法,根据主轴形状和计算精确性,选取Multi Zone 网格划分方法对主轴进行网格划分,可以自动将主轴不同尺寸轴段划分成多个独立规则区域,并对每一区域进行扫略网格划分,能够得到规则的六面体网格,相对于其他网格划分更简单便捷,图 3.5 为使用此方法获得的主轴有限元模型,共获节点84570 个,单元 74657 个。

图 3.5 主轴有限元模型
3.3 主轴的自由模态分析
机械结构的自由模态是其本身的固有属性,与外加约束和外加载荷均没有关系,由于结构本身可以看成是由无数个单元个体组成的实体,所以理论上结构拥有无数阶固有频率,在进行模态分析后,能够得到其所有频率和振型。当机械结构受到外加载荷作用时,可以根据其各阶频率来判断结构是否稳定,从而提高机械结构整体的抗振性,为设计人员在前期设备设计过程中提供参照标准和进行优化设计提供可靠依据。用户在利用有限元分析软件分析时可采用多种分析计算方法,如 Block Lanczos(分块兰索斯法)、Subspace(子空间法)、Reduced(缩减法)、Unsymmetric(非对称法)和 Damped(阻尼法)等方法,本文采用在求解大型矩阵特征值问题中最有效的一种方法 Block Lanczos(分块兰索斯法)对该主轴进行模态分析。
在 Block Lanczos(分块兰索斯法)计算自由模态时,由于主轴没有受到任何外加约束条件,所以计算结果中主轴的前六阶频率都接近于 0,振型均为刚体模态,主轴本身没有发生弹性形变,而是主轴在平面内发生平动,所以忽略主轴的前六阶低阶固有频率,提取主轴的前十二阶模态结果,频率设置范围是 0 至 10000Hz。在第七阶频率开始,才是主轴真正意义上的一阶模态频率,将第七阶频率视为主轴自由状态下的第一阶固有频率,前六阶频率值见表 3.3,各阶振型见图 3.6。
表 3.3 不加约束的主轴前六阶固有频率和振型

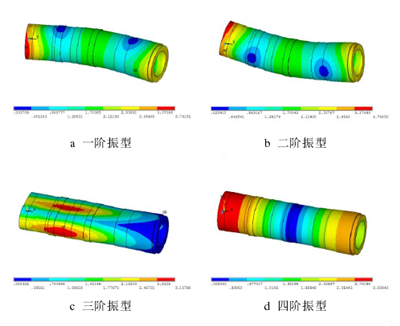
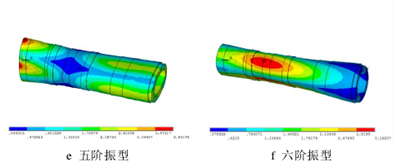
图 3.6 不加约束的主轴前六阶振型
从主轴模态分析结果可以看出,主轴的一阶和二阶固有频率相近,并且其振型表现为正交,因此可将其视为复根,主轴的第一阶模态表现为主轴的垂直方向(Y 向)上的一阶弯曲振动,第二阶模态表现为主轴横向水平方向(Z 向)的一阶弯曲振动,且最大弯曲变形均发生在主轴的两端。第三阶模态表现为扭转,没有发生弯曲变化。主轴的第四阶、第五阶和第六阶均发生了径向扩张或收缩。
3.4 考虑轴承刚度的主轴模态分析
由于主轴在工作过程中并不是单独运动,而是受到主轴系统中其他部件提供的外加载荷影响,如支撑系统的刚度,在本课题研究的数控螺纹修复车床中,主轴回转运动是机床的主运动,主轴回转运动同时带动轴承内圈一起做回转运动,因此,轴承的支撑刚度对主轴系统的动态性能影响极大。一般设计人员在做这类主轴的动态特性分析时往往会把轴承的支撑刚度考虑进来,从而更加真实准确的模拟在实际工作状态下主轴的动态性能,下面就分析该主轴在考虑轴承支撑刚度约束条件下的动态性能。
3.4.1 结合面的处理
机械系统往往由多个零部件组成,在对机械结构进行有限元建模时也要考虑到部件或零件之间的相互影响,因系统部件或零件之间存在相互作用力,对彼此的动态性能产生影响,所以在对机械结构进行动力学特性分析时要考虑到这个影响因素。我们称机械结构系统部件或零件之间相互接触的面为结合面,对结合面如何进行适当处理一直以来都是有限元动态分析的难点。在有限元模型中,结构系统的部件可以根据需要划分成若干个子结构,处理结合面问题就是处理子结构之间的相互影响,实际部件之间的结合面结构是非常复杂的,但在有限元分析中,通常将结合面简化为若干个连接点来处理,通过不同数目的结合点,结合点的自由度情况以及具体的结合条件来描述不同的结合状态。根据子结构结合面是否有相对运动,可将结合状态分为刚性结合和柔性结合[36,37]。
两个子结构接触面没有相对移动,即结合面上的对应接触点位移始终保持相对静止,这样的结合成为的刚性结合。这时接触面上的数学模型为:
位移对应关系:
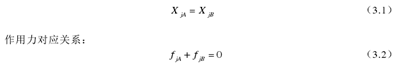
在刚性结合中,事实上,结合点就是子结构结合面之间对应的无数结合点被人为假设分开后形成的,对于这样的连接处理较为简单,在结合处对所要分析对象施加外载荷即可模拟相互之间的影响。柔性连接则较为复杂,在机械结构实际工作过程中,零部件连接部分通常会发生振动而产生微小的相对运动,如旋转轴与轴承之间的连接,部件之间的螺钉连接等情况。对于本课题研究的主轴系统,当机床工作运转时,主轴及主轴的支撑系统都会发生振动,即主轴与轴承之间的结合面会发生相对运动,在这过程中,储存能量与消耗能量交替进行,兼具弹性与阻尼特征。在处理结构的柔性连接问题时,通常采用弹性元件和阻尼元件来模拟这类连接问题,即在每一个结合点的每一个运动方向,同时用一个弹性元件和一个阻尼元件来模拟运动情况。
如图 3.7 所示为本文简化的主轴结合部模型,系统由外加载荷 F 作用在 A 结构上的 G 点,A,B 结构之间的相对运动情况利用一定数目的等效弹簧和自阻尼器来模拟,这种连接情况即为柔性连接。
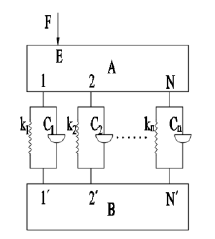
图 3.7 结合部简化模型
3.4.2 单元选择和约束限制
在主轴的实际工作时,轴承支撑对其有柔性约束作用。有限元分析软件中提供了模拟类似柔性约束的单元来进行模拟分析其动态特性。通常选用 GOMBIN14 单元来模拟主轴与轴承的结合面相对运动情况,其几何形转、节点方向及坐标轴方向如图 3.8所示,GOMBIN14 单元在二维空间上具有两个自由度,可以在任意两个节点连接方向上传递载荷,同时其具有两个节点以及一个定向节点。GOMBIN14 单元不具备弯曲和扭转,只考虑其轴向的伸缩变化,本身不具备质量。
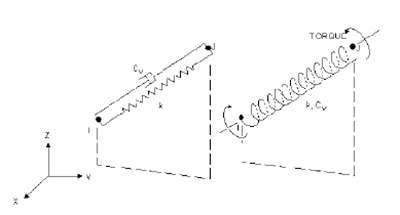
图 3.8 GOMBIN14 的几何形状
由于 GOMBIN14 单元不具有质量,为了模拟轴承及其附加件对主轴动态特性的影响,有限元分析软件还提供了 MASS21 质量单元来模拟轴承及其紧固件来添加质量,其空间形状如图 3.9 所示。MASS21 质量单元在三个方向上的坐标轴上共有六个自由度,并且每个方向都有质量和转动惯量,通过赋值实常数即可实现模拟。
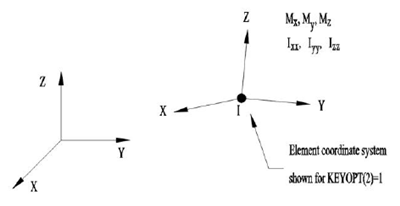
图 3.9 MASS21 的几何形状
上文已经对该主轴划分网格完毕,得到了自由状态下主轴的精确六面体网格划分结构,并对材料属性参数进行赋值。在考虑轴承支撑刚度条件下,需要对主轴设置外加约束限制,以模拟轴承与主轴结合面的实际工作情况。为了更加真实的模拟轴承对主轴的约束情况,将自由状态下划分网格完毕的主轴模型保存成.inp 格式的文件,利用有限元分析软件强大的数据对接功能,将文件再次导入,以精确添加轴承的约束条件。通常将轴承及其紧固件视为在圆周方向等效分布的四个弹簧 ,用弹簧阻尼单元GOMBIN14 模拟轴承的支撑[38],轴承分布图如图 3.10 所示,图中 T1、T2、T3、T4 四个节点为轴承与主轴截面相结合的节点,T5、T6、T7、T8 四个节点为轴承的另一端,为了限制主轴的轴向方向的移动,在节点 T1、T2、T3、T4 施加轴向约束,限制其轴向自由度,弹簧的另(T5,T6,T7,T8)为固定约束,约束其全部自由度。
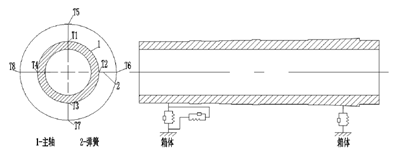
图 3.10 弹簧的分布示意图
本文主轴后端由两个圆锥滚子轴承支撑,前端由一个双列圆柱滚子轴承支撑,所以轴承约束共由 20 个 GOMBIN14 单元和 20 个 MASS21 质量单元模拟实现。图 3.11即为添加轴承约束条件后的主轴有限元模型。
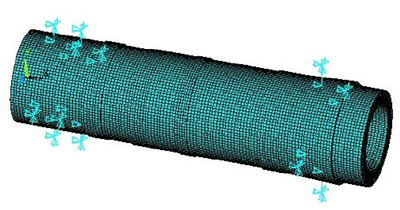
图 3.11 添加约束的主轴有限元模型
3.4.3 轴承的刚度计算
主轴工作过程中受到轴承的支撑作用,二者之间结合面为柔性结合,因此在对主轴进行有限元模态分析时,一定要考虑轴承支撑刚度对主轴动态特性的影响,下面就对本课题研究的数控螺纹修复车床所选用的轴承进行刚度计算,为下面的主轴模态分析提供参数具体数据。
(1)轴承具体参数
本主轴所选用的轴承为一对圆锥滚子轴承和一个双列圆柱滚子轴承,其型号分别为 HR2-32960-P5 型圆锥滚子轴承和 NNU4064KM/W33-P5 型双列圆柱滚子轴承。滚子轴承有很多参数,所以在表 3.4 中列出滚子轴承所需的各项参数及其代表内容。
表 3.4 轴承参数
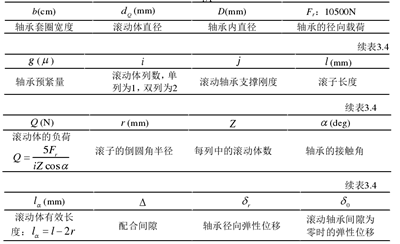
表 3.5 列出了轴承游隙为零时的各类滚子轴承其弹性位移的计算公式:
表 3.5 滚动轴承游隙为零时的弹性位移计算公式
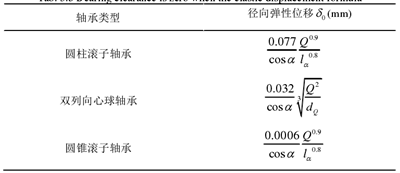
(2)计算圆锥滚子轴承刚度:
下面分别计算圆锥滚子轴承和圆柱滚子轴承的支撑刚度,表 3.6 列出了本文支撑主轴所选用的单列圆锥滚子轴承 HR2-32960-P5 各项参数。
表3.6 圆锥滚子轴承具体参数



(3)计算圆柱滚子轴承支撑刚度:
表 3.7 列出了 NNU4064KM/W33-P5 型双列圆柱滚子轴承的各项参数。
表3.7 圆柱滚子轴承具体参数





3.4.4 考虑轴承支撑刚度的模态分析
主轴的振动可以看成是每阶振型的线性组合,其结构为连续体,因此理论上主轴存在无数阶固有频率,但在实际加工过程中低阶固有频率对轴的振动影响要比高阶固有频率大,因此低阶频率对轴的动态特性起决定作用[40,41]。表 3.8 是应用有限元分析软件计算出的主轴在轴承约束条件下的前六阶固有频率及振型,图 3.9 为前六阶的阵型图。
表 3.8 弹性约束的主轴前六阶固有频率和振型

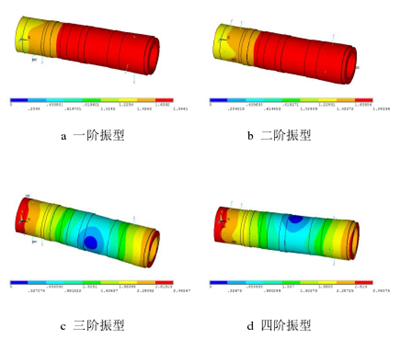
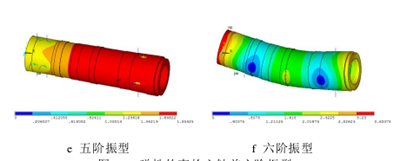
图3.12 弹性约束的主轴前六阶振型
从主轴的固有频率表和振型图可以得出,主轴的一阶、二阶固有频率相同,三阶、四阶固有频率相近,并且其振型表现为正交,因此可将其视为复根。主轴的第一阶模态表现为主轴的垂直方向(Y 向)上的一阶弯曲振动,且最大形变量为 1.84mm;第二阶模态表现为主轴横向水平方向(Z 向)的一阶弯曲振动,且一、二阶最大弯曲变形发生在主轴的中部,最大形变量为 1.84mm;第三阶模态表现为主轴垂直方向(Y 向)的二阶摆动弯曲振动;第四阶模态表现为主轴的横向水平方向(Z 向)的二阶摆动弯曲振动,且三、四阶最大弯曲变形均发生在主轴两端;第五阶模态表现为扭转;第六阶模态表现为主轴的垂直方向(Y 向)上的三阶弯曲振动,最大变形发生在主轴左端。
3.5 主轴临界转速分析
主轴回转工作时,有时主轴的挠度会迅速增加,并且主轴转动发生波动,此时主轴的转速即为临界转速[42]。主轴工作时的转速应尽量避免接近临界转速,从而避免发生共振情况。通过比较临界转速与主轴工作转速,可以判断主轴系统是否发生共振,转速和频率的关系如式(3.3)所示:

表3.9 主轴前六阶固有频率的临界转速
3.6 主轴的谐响应分析
3.6.1 主轴切削力计算
在主轴回转运动过程中,受到来自外部载荷的激振作用,同时由于自身做回转运动,所以会受到外部激振力的周期性激振作用。主轴受到的外部载荷主要来自机床刀具切削工件时的切削力作用,研究切削力对主轴的动态响应问题至关重要,下面就对本课题主轴受到的切削力进行计算,为研究主轴的动态响应问题做铺垫。

3.6.2 主轴谐响应分析
在机床加工过程中,主轴会受到外部力周期激振作用,当主轴的固有频率与激振频率相等时就会发生共振现象,不但会降低机床的加工精度,同时还会损害加工刀具和机床本身[43]。因此,研究结构的动态响应是动力学分析问题中至关重要的内容。谐响应分析是以模态分析为基础,主要研究当外载荷为随时间变化而呈现简谐变化作用在线性结构上时,结构有何稳态响应[44]。本文采用模态叠加法,将模态分析结果中得到的各阶振型分别乘以对应系数,之后求和求解动力学响应问题。本文将切削力作为激振力,对主轴施加 530N 的激振力,加载在主轴前端轴承支撑中点处,频率范围为频率范围为 0-2000Hz,研究主轴径向方向的动态响应情况,图 3.13 为得到的幅频曲线图。 3.13图3.13 主轴前端幅频曲线图
从图 3.13 中可以看出,当激振频率在 465Hz 附近和 689Hz 附近时,主轴的径向位移出现峰值,且在 689Hz 附近时峰值最大,此时主轴的动刚度最小,当激振频率在 0至 400Hz、620Hz 附近及大于 800Hz 时,主轴的径向位移均很小,说明在这些频率范围内主轴由较好的动刚度。
3.7 本章小结
本章介绍了该主轴系统的具体结构,对其进行了简化处理。利用三维建模软件进行实体建模,并导入有限元分析软件进行网格划分,之后进行分析。先对主轴进行了自由状态下的模态分析,得到了主轴的固有频率及振型。再考虑主轴在约束条件下的动态特性,介绍了结合面的处理方法,并具体模拟了轴承对主轴支撑结合面的限制情况,利用数学方法计算得到了支撑轴承的具体刚度,对主轴进行模态分析,得到了在考虑轴承支撑刚度约束条件下的主轴振动频率,并将振动频率与主轴的极限转速作对比分析,了解到主轴振动频率远远低于其共振区域。最后分析了主轴的动态响应特性,为后面对主轴进一步优化设计打下理论基础。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
专题点击前十
| 更多










