车削用电主轴永磁同步电机电磁与热特性的研究(中)
2017-2-10 来源:沈阳工业大学 作者:闫佳宁
3.1 车削用电主轴永磁同步电机的弱磁问题
3.1.1 永磁电机弱磁原理
电励磁同步电动机可以通过调节励磁电流增大其恒功率运行范围,而永磁同步电机是由永磁材料提供励磁,磁场恒定,励磁强度不可调节,转子磁场在定子电枢绕组内感应的反电动势与电机转速成正比,当电机端电压随转速升高到变频器能够输出的最高电压之后,电机的转速会受到限制,若要继续升高电机转速则需要对气隙磁通进行削弱,即需要对电机进行弱磁控制以维持反电动势的平衡,扩大电机的速度范围,此时电机将不再做恒转矩运行。


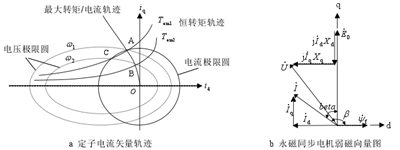
图 3.1 弱磁控制原理图


3.2 车削用电主轴永磁同步电机的弱磁计算分析
3.2.1 弱磁磁路特性分析
对电机模型进行静态场仿真分析,考察当不注入弱磁电流,额定电流 50A 加载在交直轴不同位置时,电机的空载磁场、直轴电枢反应磁场、交轴电枢反应磁场、某负载磁场四种情况下的磁场分布,旨在比较不同情况下的磁场特点并得出结论,为弱磁下的转速分析做铺垫。

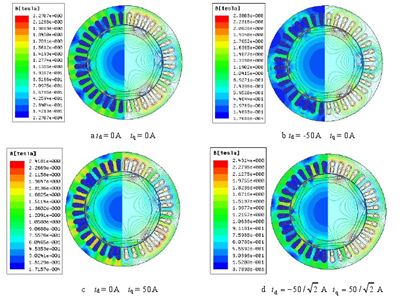
图 3.2 不同情况下磁场分布
比较图 3.2 a 和 b 发现,当电流分量全部加载在直轴上,id 为负时,电机齿部和轭部磁密减小明显,处于去磁状态;比较 a 和 c 发现,当电流分量全部加载在交轴上时,c 中磁力线较 a 发生了畸变,这说明 iq 的作用为使磁力线产生畸变;a、b、c 的比较表明,电机运行过程中定子电流的交直轴分量不断变化,使 d、q 轴之间存在交叉饱和影响,这会给 Ld 的计算带来困难。此外永磁体不同的放置方式和磁极形状的灵活多变,也使电机的交、直轴电感参数与电流的关系呈现出非线性[46,47]。所以,要准确分析永磁同步电动机弱磁扩速的性能,在计算电机参数时就要充分考虑交叉饱和和非线性的影响,采用场的方法研究电机的电感参数便非常必要。
3.2.2 基于有限元的交直轴电感参数计算
传统的等效磁路法计算电感需要改变转子位置,求得定子各相绕组的自感和互感随转子磁路变化的关系,对于不同的永磁体放置方式,还需进行修正,计算过程相对复杂,如果修正系数选择不当还将影响计算的准确性[48]。Maxwell 静态场法对电机的电感矩阵的仿真计算是基于特定激励且针对完整闭合绕组,因此需要在设置前确定 6 极 36 槽电主轴电机的每个绕组的回路关系及匝数Turns,完成电感矩阵 Matrix 的设置。各绕组回路连接后再将属于同一相的绕组归为一组,并设置并联支路数 Branches。然后设置不同的 id 和 iq 求得不同情况下的三相电感值 LABC,通过变换即可求得 d、q 轴电感值,具体做法如下。

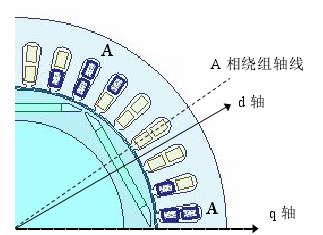
图 3.3 初始时刻位置示意图




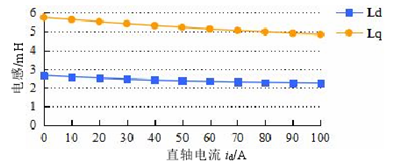
图 3.4 id 对电感影响
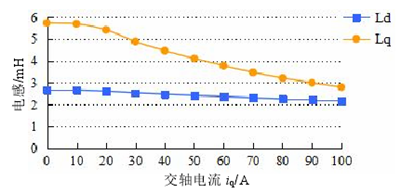
图 3.5 iq 对电感影响

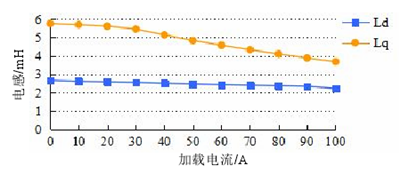
图 3.6 id 与 iq 对电感影响
从上面的分析看,无论是单独施加 id 分量还是 iq 分量,Ld 均变化不大,但 Lq 的反应很敏感。在电机的实际控制中,根据最大转矩与电流比的矢量控制方式,交直轴电流是同时存在的,所以在分析时要考虑到交直轴电感之间的耦合问题。
3.2.3 弱磁控制下的速度校核
根据上面分析阐述,本课题所用电主轴电机在达到转速拐点之后采用弱磁控制,弱磁时能达到的最大电流为 100A,由上文分析可知,当电流全部位于直轴时,电机能达到此种控制下的最高转速,现对其理想状态下的弱磁最大速度进行分析。当 id= -100A,iq= 0A 即电流分量全部为直轴分量时,在静态场中计算得到三相电感矩阵为
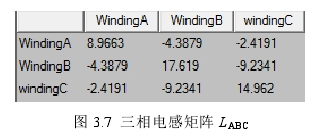

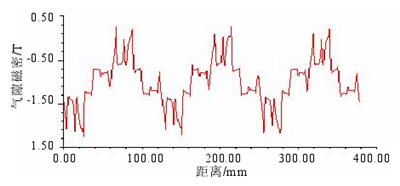
图 3.8 弱磁时径向气隙磁密

300Hz,并带有待确定控制角 beta 的电流源,对 beta 进行参数化,以找到合适的角度使得电机输出能够达到二倍弱磁速度时所对应的转矩。当 beta 在 0°~90°之间、以 10°为步长时,输出的转矩如图 3.9 所示。若能达到二倍弱磁速度则电机输出的转矩应该为 44.6N?m 左右,从图中可以看出当 beta 在 80°~90°之间时平均转矩为-0.0514N?m~54.5645N?m,涵盖了目标转矩,则将 beta 定位于 80°~85°度继续细分进行参数化,发现当 beta=81.8°时对应的输出转矩为 44.85N?m,即寻找到了合适的控制角 beta 使电机输出二倍弱磁速度对应的转矩,说明电机能够达到二倍弱磁速度,此时的控制角为 81.8°。图 3.10 为控制角 beta 与转速的关系。
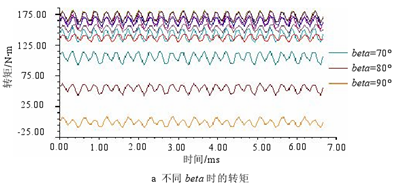
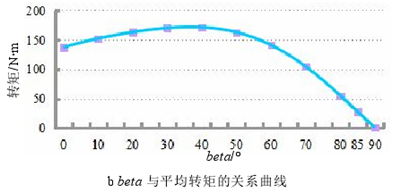
图 3.9 不同 beta 对应的转矩
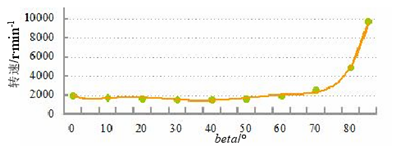
图 3.10 不同 beta 与转速的关系
从图 3.10 中可看出当控制角超过 70°后转速有所上升,在输出结果中得到当控制角为 81.8°时转速可达到 6000r/min,可以满足满足车削加工中二倍调速的需求。
3.3 车削用电主轴永磁同步电机的损耗计算
3.3.1 损耗计算方法
(1)铁耗计算
1)传统铁耗计算模型
电机铁耗包括基本铁耗和空载铁心附加损耗,基本铁耗又包括磁滞损耗和涡流损耗。传统计算方法是将铁心的磁滞损耗和涡流损耗以总和的形式计算,计算公式为

电机运行时旋转磁化主要发生在轭部,交变磁化主要发生在齿部,二者性质不同,需要将轭部损耗和齿部损耗分别计算,所取 B 为轭部磁路磁通密度最大值,齿部磁路磁通密度平均值。齿部与轭部
ak 的取值也有所不同,但都是将磁通密度分布不均匀、磁通密度随时间不按正弦变化(即谐波磁场产生的附加铁耗)、机械加工等多种因素考虑在内的经验系数。对于空载铁心附加损耗通常不做详细计算,而是根据不同类别不同容量规定其为输入功率一定的百分比。在工厂计算中则是通过取更高的 ka 来计及空载铁心附加损耗的影响。由此可见,电机传统铁耗计算模型虽然使用起来简便实用,但往往依赖于经验系数的取值,在车削电主轴电机设计研发初期不适宜采用。
2)基于有限元法的 Bertotti 铁耗分离计算模型
目前利用有限元法计算电机铁耗所采用最多的模型为 Bertotti 铁耗分离模型,上述提到传统方法中计及磁密不均、磁密非正弦变化、机械加工影响硅钢片导磁性能等多种因素对损耗结果的影响是通过引入经验系数实现的,而有限元法可通过对得到的铁心内部任意区域的磁密或计算模型的处理计及上述因素。Bertotti 铁耗分离计算模型由 Bertotti 于 1988 年提出,是根据损耗的不同产生机理将其分别加以计算,因而得名铁耗分离计算模型。在正弦磁通下,由磁滞、涡流及附加损耗组成的三项式铁损模型可表示为[49-51]





3.3.2 额定与弱磁时的损耗比较分析
(1)定子铁耗的有限元计算
目前大多数文献采用有限元法计算铁耗时都采用 2D 计算,其精度已经能够满足要求,且 3D 计算占用资源过大,没有必要采用。在计算定子铁心损耗前,首先要确定铁心损耗系数,本课题所设计样机定、转子均选用 DW310_35 型号硅钢片材料,其 50Hz、60Hz、100Hz、200Hz、400Hz、1000Hz频 率 下 的 B-P 曲 线 及 拟 合 曲 线 如 图 3.11 所 示 。 拟 合 后 得 到 损 耗 系 数 值 为 :
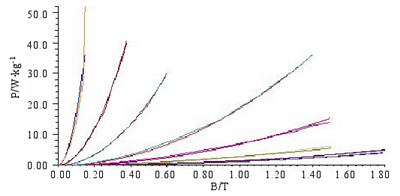
图 3.11 硅钢片材料 B-P 曲线
对第 2 章所设计的 6 极 36 槽车削电主轴电机模型的轭部和齿部进行分割(分割线与槽底有适当距离),在额定转速 3000r/min、额定电压运行情况下进行时步有限元仿真,分别得到定子轭部和齿部的铁心损耗,计算结果如图 3.12 所示。图 3.13 为弱磁条件下损耗的计算结果。
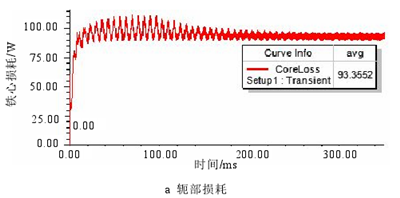
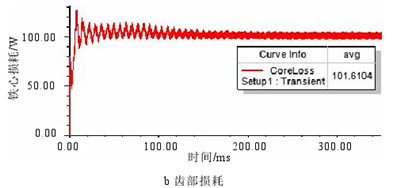
图 3.12 额定时定子铁心损耗
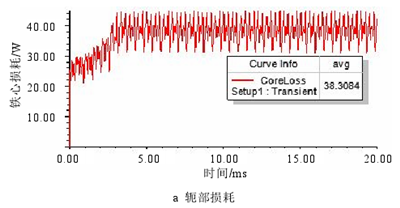
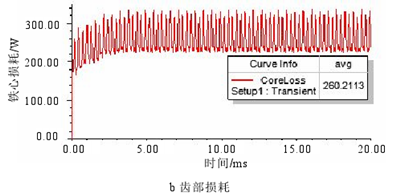
图 3.13 弱磁时定子铁心损耗
当转速 6000r/min,电流有效值 100A 弱磁时,从图 3.13 中可以看出在铁耗平均值稳定后幅值变化较大,这是因为弱磁控制时谐波增大造成的。且对比额定时的铁耗可以发现,轭部铁耗减小,齿部铁耗增大,与磁密分析的结果一致。此外,弱磁时的总损耗也较额定时有所增大。
(2)杂散损耗的计算
电机损耗包括四类:铁耗、铜耗、机械损耗和杂散损耗。前三种损耗的计算方法在上文已经有所阐述,对于本课题所研究的车削电主轴电机,杂散损耗以转子铁心损耗和永磁体涡流损耗计。额定和弱磁时经有限计算得到的转子铁心损耗和永磁体涡流损耗如图 3.14 和图 3.15 所示。可以看出,额定甚至在弱磁运行时转子铁心损耗和永磁体涡流损耗都不大,额定时转子铁心损耗和永磁体涡流损耗分别占额定功率的 0.03%、0.01%,弱磁时两者分别占额定功率的 0.14%、0.01%。综合以上分析计算,将损耗结果在柱状图 3.16 中进行表示。
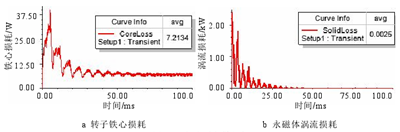
图 3.14 额定时杂散损耗
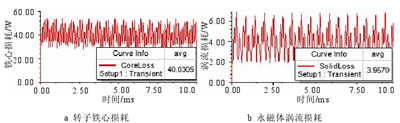
图 3.15 弱磁时杂散损耗

图 3.16 额定与弱磁时的损耗对比图
从图 3.16 中可以直观看出二倍弱磁速度时定子轭部铁耗减小了 59.0%,定子齿部铁耗增大了 156.1%,绕组铜耗增大了 300.0%,转子铁耗增大了 456.7%,永磁体涡流损耗增大了 58.4%,但转子铁耗和永磁体涡流损耗其值本身很小,对于功率不大、非高频的永磁电机若不做特殊研究需求,对于总损耗的影响可以忽略不计。
3.4 本章小结
本章比较系统的对车削用电主轴的弱磁问题和损耗计算进行了阐述分析,总结如下。
(1)从弱磁原理出发,分析了提高电机弱磁速度的方法,并对交轴电枢反应和直轴电枢反应时的磁路特性进行分析,发现 d、q 轴之间的磁路存在交叉饱和影响,直轴电流 id 的作用是使磁路去磁,交轴电流 iq 的作用为使磁力线产生畸变;随后基于场计算得到随 id 与 iq 增大,直轴电感 Ld 和交轴电感 Lq 都有所下降,但 Ld 随电流变化不大,L
q 对电流变化表现得很敏感;通过场计算得到此未经特殊设计的电机 Ld 的值为3.32m H,进而通过解析公式计算出所设计电机在电流全部在直轴上时,能达到的最高转速为 6936.4r/min 后,采用有限元计算进行验证,找到当 ilim=100A,控制角 beta=81.8°时,能够达到所需二倍弱磁速度 6000r/min。
(2)介绍了电机铁耗,铜耗,机械损耗以及杂散损耗的计算方法,并基于有限元求得了电机的额定时的定子铁耗约为 195.0W,弱磁时约为 298.5W,增加了 53.1%;额定时铜耗约 687.9W,弱磁时因电流为额定的二倍,铜耗变为原来四倍;额定时转子铁耗约 7.2W,弱磁时约 40.0W,增加了 455.5%;额定时永磁体涡流损耗约为 2.5W,弱磁时约为 3.96W,增加了 58.4%。此外,杂散损耗为转子铁耗和永磁体涡流损耗,其值与其它损耗相比很小。
第 4 章 20k W 水冷样机的温升计算与实验对比
电机稳定运行一段时间后温度也趋于稳定,其稳态温升和温度最高点直接影响电机的运行可靠性和使用寿命,温升过高会引起绝缘老化、永磁体退磁,准确计算电机的温度场分布规律对电机冷却系统的设计、降低电机温升、合理选取绝缘材料都具有重要意义。
本章对一台 20k W 水冷样机进行温度场仿真计算,然后将计算结果与其实验数据做对比,从而验证本章计算方法对于此类电机温度场计算的准确性,其中包括建模简化时绕组的等效方法、导热系数的选取、热源加载、装配间隙等关键步骤的处理。
4.1 温度场计算的数学模型
电机内定子铁心、绕组、轴承等部件的发热情况不尽相同,便引起了热量的传递,尽管热量传播的过程十分复杂,但一般总先由发热体内部借传导作用传到发热体表面,然后在通过对流和辐射作用散到周围介质中,传递时不仅需要满足能量守恒、动量守恒和质量守恒定律,还要满足热传导方程。根据传热学的基本理论,在直角坐标系下,电机内的稳态温度场求解可归结为如下边界问题[52]。

4.2 20k W 水冷样机热计算的前处理
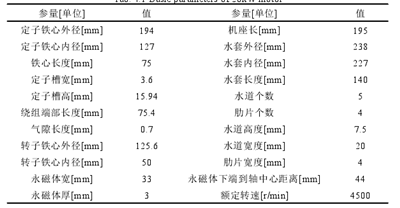
20k W 水冷永磁同步牵引电机的基本参数见表 4.1。本课题温度场的计算是基于有限体积法,用 Solidworks 建立电机的三维模型时为方便求解域的建立,应对模型做适当简化(确保不改变物理过程),否则剖分质量难以达到计算要求,会给温度场分析带来不便。
表 4.1 20k W 样机基本参数表
4.2.1 三维求解域的建模与简化
(1)转子铁心的简化建模
如第 3 章所阐述,样机中的实心块状永磁体存在涡流损耗,硅钢片叠压的转子铁心存在铁心损耗,两者即是热源又是导热媒介,建模时应尽可能接近实际模型。内置“V 一”型永磁体结构较为复杂,端部存在不规则形状的窄尖隔磁桥,建模时进行如图 4.1 所示的简化,这样处理既能提高部分质量,又能尽可能的接近实际情况。
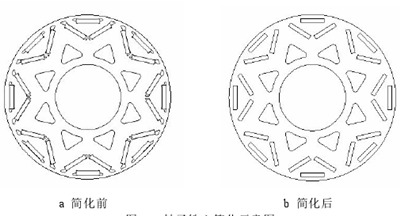
图 4.1 转子铁心简化示意图
(2)槽内所有绝缘和绕组端部建模的简化方法电机定子槽内绝缘组成复杂,有绕组股线绝缘(绝缘漆膜)、槽绝缘和层间绝缘、浸渍漆,建模和剖分时无法完全考虑,因而通过如下假设将其化为等效槽绝缘。
1)铜线的绝缘漆分布均匀;
2)槽绝缘和层间绝缘填充均匀;
3)电机浸漆状态良好,浸渍漆填充均匀;
4)槽内绝缘与定子铁心及绕组紧密接触。其厚度计算方法如流程图 4.2 所示。
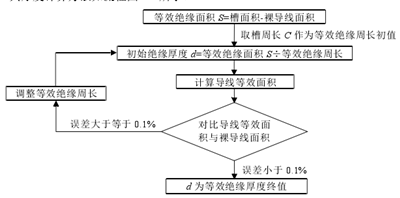
图 4.2 等效槽绝缘厚度计算方法
对于双层绕组,在计算导线等效面积时注意保证上下层导线面积相等且等效槽绝缘厚度均为 d。经计算,样机的等效绝缘厚度为 1.21mm,其示意图如图 4.3 所示。

图 4.3 槽内绕组及绝缘的等效模型
此外,绕组端部采用直线来等效其实际排布,因为物体的温升与其散热面积、散热系数、热流密度以及周围环境有关,而与物体形状无关。
(3)端盖、转轴等其余部件的简化建模
端盖和转轴自身不产生热量,仅作为导热媒介,且电机大部分热量由机壳与水套中所流通的冷却水带走,所以为提高剖分质量,将端盖圆倒角简化为直角,仅保留转轴与端盖、转子、轴承接触部位的台阶。
此外,将电机固定所用的紧固螺钉、扣片与其相接触部件融合为一体。在定子铁心端部有定子绝缘端板,转子铁心端部有转子压板,它们所用材料的导热系数与端部静止的空气非常接近,故将定子绝缘端板和转子压板省略按空气处理。鉴于本台电机是圆周对称结构,又考虑到计算机配置和计算时间等问题,按上述处理后建立电机的 1/8 模型如图 4.4 所示。
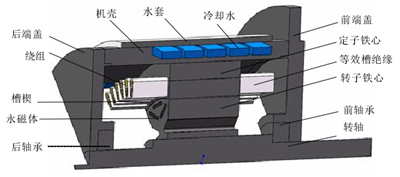
图 4.4 20k W 水冷样机三维温度场的求解模型
4.2.2 求解模型的剖分与边界条件
(1)模型的剖分
流体与温度场计算中,网格剖分关系着计算的收敛性和结果的准确性,可以说占据了流体与温度计算百分之七十的工作量。剖分时六面体网格与四面体网格相比具有显著优势:六面体网格更能迎合流场方向(如边界层处),离散误差小;剖分同样网格尺寸时数量少,计算时间短。此外,结构化网格网格点之间的邻近关系有序且规则,计算效率比非结构化网格高,故在进行对网格质量要求比较高的流体与温度场计算时,尽量剖分为结构化六面体网格。
电机内部气体分布极其不规则,为提高剖分质量,有时需要切分为规则整块进行剖分。对于出现圆弧的部件,可以先对面进行四面体剖分,再用扫掠剖分为六面体。此外,流体场变化大的地方需要细剖比如气隙等,流体场变化小的地方可以适当粗剖,比如端盖等,在不影响计算精度的情况下,合理布置网格,是提高网格划分质量的关键。但剖分尺寸不宜相差过大,网格越均匀,计算越容易收敛。在前处理软件 Gambit中剖分后,电机各部位的剖分尺寸如表 4.2 所示。
表 4.2 20k W 样机各部位剖分尺寸表
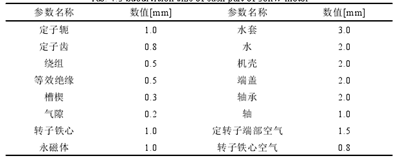
图 4.5 为网格质量 Equisize Skew 的检查结果,对各部件单独检查发现只有槽楔和轴的失真度较大为 0.68,其余部分失真度比其更小,剖分效果理想,整机剖分结果和气隙剖分结果如图 4.6 所示。
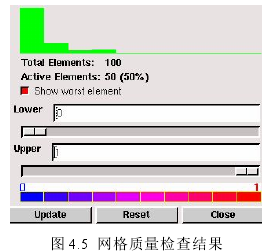
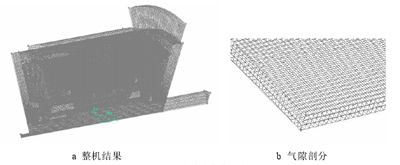
图 4.6 20k W 水冷电机剖分结果
(2)模型的边界条件
根据电机系统结构特点以及整域传热特性,求解域内具体边界条件设置为:
1)将 1/8 模型的切面设置为绝热 WALL 边界;
2)电机外表面设置为绝热 WALL 边界;
3)其余互相接触且外圈轮廓形状一致的一对面设置为 INTERFACE 耦合边界。要注意设置耦合面的正确性,否则将得到错误的温度分布。
4.2.3 各部位传热系数的确定
电机内部的热传递主要靠热传导方式实现,不同材料的部件传递热量的能力也不同,传热系数的准确确定是温度场计算的前提条件。样机中部分导热系数依据材料的固有属性确定,部分传热系数需要根据等效方法进行相应计算。
(1)气隙等效传热系数的计算
转子旋转使气隙内空气对定转子交换热量的能力强于静止状态。引入有效传热系数λeff 来描述气隙中流动空气的热交换能力,即单位时间内静止流体在定转子之间所传递的热量和流动空气所传递的热量相等,这样可把旋转的转子视为静止不动处理[54,55]。根据文献[55],假设定子内表面和转子外表面为光滑圆柱面,则气隙中的雷诺数为

(2)定转子铁心叠片等效传热系数的计算
样机的定转子铁心由硅钢片沿轴向叠压而成,由于工艺限制,片与片之间不能紧密贴合,导致叠片之间存有空气,且铁心叠片在加工过程中会对铁心进行浸漆,使其传热系数远小于纯硅钢片的导热系数,这也导致了铁心叠片在 x 方向、y 方向、z 方向传热的各向异性。为此,本课题采用轴向等效传热系数计及硅钢片漆和空气对铁心叠片的影响。由相关文献知,定子铁心轴向等效传热系数的计算式为

(3)等效槽绝缘传热系数的计算
定子槽内绝缘组成比较复杂,含有导线漆、浸渍漆、槽绝缘材料,为了便于计算等效槽绝缘的传热系数,做如下假设:
1)忽略股线间由于绝缘漆膜存在造成的温差;
2)认为定子槽内绕组的发热均匀,忽略绕组的集肤效应。
按照 4.2.1 中的方法将定子槽内的绝缘等效成一个实体后,其等效传热系数可以由公式(4.7)确定。

(4)各实体材料的导热系数
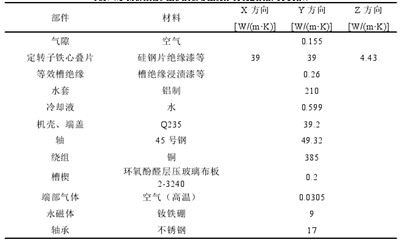
以上计算得到的气隙等效传热系数、定转子铁心叠片等效传热系数、等效槽绝缘的传热系数,同样机内其余各部件所采用的材料及其导热系数罗列在表 4.3 中,数据来源于《Y2 系列三相异步电机技术手册》和魏永田的《电机内热交换》。表中数据为考虑定转子铁心叠片的各向异性,气隙、等效槽绝缘、绕组、空气、轴承等介质的各向同性的数据。此外,对于封闭式电机,绕组端部可以当做自然散热处理,取高温空气的导热系数进行计算。
表 4.3 20k W 电机各部分材料及传热系数
(5)机壳表面散热系数的处理
依据《电机内热交换》,考虑样机内有气体循环,用式(4.8)计算机壳表面散热系数。

4.2.4 装配间隙的处理
电机部件间存在装配间隙,如机壳与定子间、转子与永磁体间、转子与轴间、端盖与轴承间、端盖与机座间、端盖与轴间。装配间隙相当于静止的薄空气,其导热系数远不及实体材料,故对电机的最高温升影响很大,在电机温度场计算中需予以考虑。建模时无需把装配间隙建成实体,只需在 Fluent 中找到相应部位的装配间隙,并设置厚度和导热系数。机壳与定子间的装配间隙用公式(4.9)计算。
计算得到定子铁心与机座的装配间隙为 0.0000113m。此间隙的空气温度仅略大于环境温度,取低温下空气导热系数,为 0.0242W/(m.K)。而转子铁心与永磁体的装配间隙为 0.0001m(工艺引起,根据公差带相减平均而得)。转子铁心与永磁体间隙温度较高,取高温空气的导热系数 0.0305W/(m.K)。其余部分类似,得到表 4.4[56]。
表 4.4 装配间隙明细表

4.3 20k W 水冷样机的稳态温度场计算
4.3.1 求解初始条件
(1)给定环境温度为 27℃(300K)。
(2)给定速度入口 VELCITY_INLET,水速为 1.975m/s(即实验水速)。
(3)给定压力出口 PRESSURE_OUTLET,零相对压力,即一个标准大气压,101325Pa。
(4)水力直径若为圆形管道,则水力直径 D 为圆形管道直径,若流体流动的界面为其它形状,那么可由下式求得等效水力直径 DH
其中,A 为管道截面积,U 为流体湿周。计算得到 20k W 样机的水力直径为 10.91mm。
(5)湍流强度
管道内流体与机壳和水套之间的换热属于强迫对流换热,流体的雷诺数可由下式得到

其中,lu 为流体的特征速度 1.975m/s,fv 为流体的运动黏度。
则求得冷却水的雷诺数为 26987.6。当流体的雷诺数在 2300~10000 之间时,流体处于层流向湍流过渡状态,大于 10000 时流体处于湍流状态,则样机通入的冷却水为湍流流动,其湍流强度 I 可由下式确定

计算得到湍流强度为 4.5%。
4.3.2 样机热源分布
温度场求解时有单向耦合和双向耦合两种方法。将电磁场计算中各部件的损耗结果作为温度场的热源,而两场分别进行计算,即为单向耦合方法。双向耦合是通过电磁场分析和温度场相互传递数据进行迭代,这种方法运用起来比较困难,也耗费时间。两种方法如图 4.7 所示。目前几乎所有的电机热分析都采用单向耦合,本课题也是。
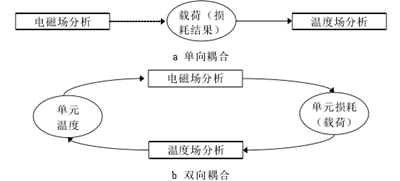
图 4.7 温度场计算方法

表 4.5 实测损耗值(环境温度 27℃)

按表 4.5 的比例进行分配,由式计算可得样机各部位的生热率如表 4.6 所示,其它部位的生热率为零。
表 4.6 各部位生热率
4.3.3 温度场计算结果与实验对比分析
经过前述简化建模、网格剖分等过程后,利用 Workbench 中的 Fluent 模块对样机进行稳态热分析,经过样机材料参数定义、边界条件设置、加载热源等步骤,在收敛达到要求精度后,迭代求解自动停止,得到电机的温度场分布如图 4.8 所示。
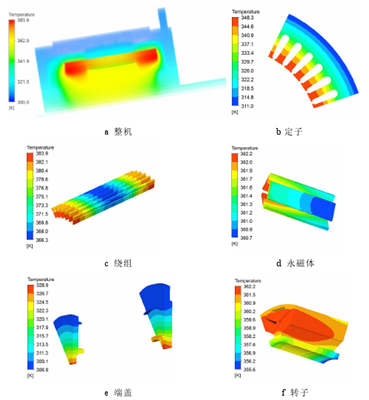
图 4.8 20k W 电机温度分布图
从图 4.8 a 中,可以看出样机的最高温升为 83.9K,且高温部分主要集中在绕组、转子铁心和永磁体处,机壳表面温升最低。图 b 中定子铁心最高温升为 48.3K,最低温升为 11K,出现了较大的温度梯度,定子齿部的温升相对轭部要高,和槽口接触的部分散热相对最差,靠近机壳和冷却水处的温度迅速降低,说明水的流动起到了良好的散热效果。图 c 中所示绕组中部散热较好而端部散热较差,最高温升 83.9K,也是样机的最高温升,并且集中在下层绕组,这是由于绕组端部由空气散热,空气的导热能力较差远不如硅钢片,热量传递较少。图 d 中所示永磁体最高温升为 62.2K,最低温升60.7K,该“V 一”结构的永磁体“一”型部分温度较低,结合图 f 可知,其热量主要热量由转子上部和气隙传递出去。图 e 中所示端盖的最高温升为 28.9K,最低温升为6.9K,端盖的最热点出现在与轴承及转轴接触的位置。从上述结果可以看出,由有限体积法计算得到的样机各部分温度都在温升限度范围内,通过埋热电偶实验测得的温升及计算结果对比如表 4.7 所示。
表 4.7 仿真与实验对比结果
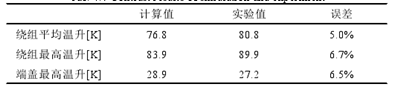
通过实验值与计算值的对比可知,该方法的误差均在允许范围内;端盖的温度分布规律与实验相符,最热点位置相同,验证了本章基于有限体积的温度场分析方法能够满足工程计算需要。
4.4 本章小结
本章以一台 20k W 水冷永磁同步样机为例,确定了电机的建模等效方法,包括转子铁心的简化建模、槽内所有绝缘和绕组端部建模的简化方法、端盖转轴等其余部件的简化建模,介绍了剖分的注意事项和技巧,边界条件的确立,气隙、定转子铁心叠片、等效槽绝缘传热系数、机壳表面散热系数的计算方法,以及装配间隙的处理等,最后用 Fluent 软件计算了电机温度场分布,与实验值进行对比,得到结论如下:
(1)由有限体积法得到的样机最高温升为 83.9K,与实验值 89.9K 的误差为 6.7%;绕组平均温升为 76.8K,与实验值 80.8K 的误差为 5%;端盖最高温升 28.9K 与实验值27.2K 误差 6.5%,验证了温度场计算方法的准确性。
(2)该样机的温升最高点位于绕组端部下层绕组处;绕组、转子、永磁体温度较高,冷却水有效通过机壳带走热量,温度梯度降落趋势合理。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多本专题新闻
专题点击前十
| 更多










