超精密车床主轴回转误差测试系统的研究
2016-12-14 来源:哈尔滨工业大学 作者:王世良
第 4 章
倾角运动误差分离及实验研究
本章将主要分析主轴倾角运动误差,在径向运动误差的基础上推导倾角运动误差求解算法;进行超精密车床主轴倾角运动误差实际测量实验,并对不同转速下主轴倾角误差运动进行研究。
4.1 倾角运动误差分析
4.1.1 轴线平均线的确定
为理解轴线平均线,我们先看一下国际机械生产研究学会(CIRP)对回转轴线的定义。1976 年 CIRP 发表了“关于回转轴性能的描述和测定”的统一文件,定义了回转轴线,即“回转轴线是一条某指定物体绕其自身旋转的线段,此线段与该指定物体一起运动,并相对于轴线平均线呈现出轴向、径向和角向的运动。”文件对回转轴的回转轴线给出了以上明确定义,但是并没有对回转中心给出明确定义[48]。
回转轴线是回转轴在任意一个瞬时具备的属性线,轴线平均线是一段时间内对回转轴线位置进行平均化得到的。在超精密车床主轴回转误差测量中,信号的同步运动误差,即是将主轴的回转误差运动作为周期性误差运动处理。在同步误差运动中,轴线平均线即为主轴周期性回转一周时,回转轴线的平均位置。

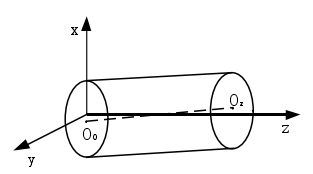
图 4-1 回转体轴线平均线模型

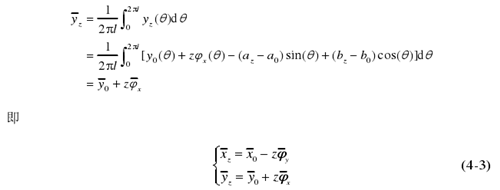
在上述方程处理过程中,我们假设回转轴的回转运动具有周期性。实际超精密车床主轴回转误差测量中,我们提取主轴的同步运动误差,实际上就是将主轴的回转误差运动作为周期性运动处理的。方程(4-3)为一空间直线方程,从方程中看出,任意截面中的任意点在回转轴回转一个周期内平均位置不变,这个平均位置点即为平均回转中心。虽然在推导过程中,应用的是最小二乘圆心,但是没有用到最小二乘圆心的任何性质,对截面内任意一点,公式依然成立。上式中的空间方程即为轴线平均线,由平均回转中心组成。
从以上分析和概念可知:已知截面内任意一点的运动轨迹,可求出此截面的平均回转中心;轴线平均线是一条空间直线,即各个截面求出的平均回转中心在一条空间直线上。所以说,已知任何两截面中任一点的运动,都可以唯一的求出回转轴的轴线平均线。而轴线平均线是求回转轴倾角运动误差的绝对参考线,每个时刻回转轴的瞬时回转轴线与平均回转轴线有一个相对位置。
4.1.2 双截面测量坐标系的相对位置
回转轴每个瞬时的回转轴线与轴线平均线有一个倾角关系。回转轴线是在双截面中的两个测量坐标系中确定的,而平均回转轴线在空间中是固定的,处于固连在大地上的绝对坐标系中。所以在计算倾角误差之前首先要明确的是测量坐标系与绝对坐标系的位置关系。
测量坐标系不能简单地理解成由传感器的布置决定,也不要简单地把三个传感器轴线的交点当成测量坐标系的原点。以下将对这两个误区进行分析。
传感器布置如图 4-2 所示,两传感器相互垂直对截面进行测量。建绝对立坐标系 2,其原点是该截面最小二乘圆心回转一周的平均位置。坐标系 1为测量坐标系。水平和垂直方向上的传感器测量值记为S1(θ) 、S2(θ)。
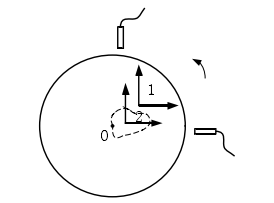
图 4-2 测量坐标系与绝对坐标系的位置关系


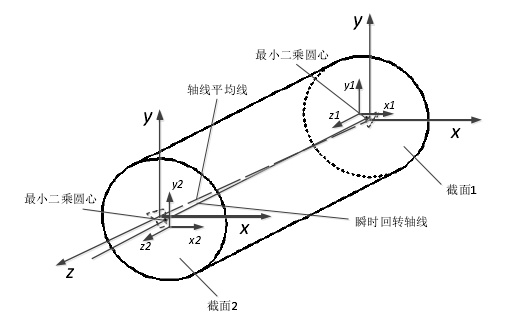
图 4-3 双截面测量坐标系与绝对坐标系的位置关系
4.1.3 倾角运动误差计算
定义回转轴的轴线平均线的意义在于给出决定倾角误差运动的参考基准,以轴线平均线建立绝对坐标系,在此坐标系中计算回转轴回转周期内的倾角运动误差。倾角运动误差即是回转轴每个瞬时的回转轴线在绝对坐标系中对x 轴和 y 的转角关系。
计算回转轴的倾角运动误差要对回转轴的两个截面的回转运动误差进行测量,对两个截面的数据进行综合处理得出倾角运动误差。当回转轴以一定转速稳定转动后,其轴线平均线在空间中是一条固定的直线,基于此线建立绝对坐标系。每个截面由传感器的安装位置各自决定此截面的测量坐标系,两个测量坐标系在绝对坐标系中处于不同的位置。
两个截面数据要进行综合处理的一个非常关键的因素是确定两个截面的测量数据要转化到一个坐标系中进行处理,否则结果就是失真的。测量数据是依赖于测量坐标系的,根据上节的结论,去掉直流分量的传感器测量值将依赖于绝对坐标系(测量坐标系与绝对坐标系重合),测量坐标系在绝对坐标系中的位置,所以可以将测量坐标系的数据转化到绝对坐标系中进行求解。
第一个测量截面为定义为基准面,在此截面上测量的径向运动误差将作为基准,通过第二个截面的径向运动误差来求得主轴的倾角运动误差。




主轴的两个截面上的径向运动误差相差很小,对于一般主轴差值是微米级,对超精密车床来说此差值的数量级都是在亚微米级。而两个测量截面的间距 l 是毫米级或是更大,所以公式(4-4)和公(4-5)可做如下简化为
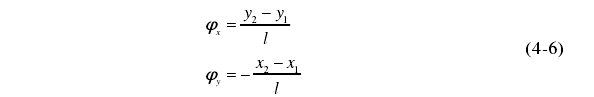
4.2 倾角运动误差测量实验及分析
4.2.1 倾角运动误差测量实验方案
倾角误差是指主轴轴线绕 x,y 轴的转动倾角,测量时要对被测试件垂直于轴线的两个截面进行同时测量。基于每个截面需要 3 个位移传感器进行径向运动误差的分离,如果进行在线时时测量,则共需 6 个传感器。鉴于实验设备的缺乏,倾角误差试验将分两步进行。
第一步,对两个截面分别进行三点法频域误差分离试验,如图 4-4。此步的目的是得到被测试件在各个截面的圆度误差,同时也能得到主轴在此截面平面内的径向运动误差。
第二步,在两个截面内的 x,y 方向上同时架设 4 个位移传感器,对主轴的误差运动进行测量,如图 4-5,数据处理将在下面的小节中详细介绍。

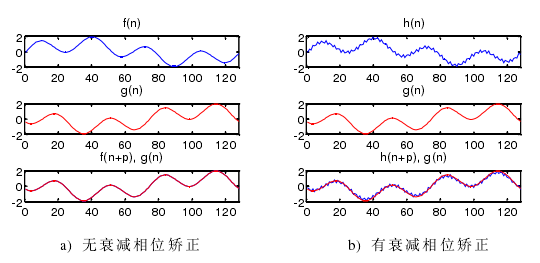
图 4-6 相位矫正
4.2.2 相同点位非同时测量值的相位矫正
因为倾角运动误差需要分两次测量,而且本实验所用超精密车床的编码器是增量式而非绝对式的,给实际测量实验带来了一定困难。本节将研究传感器在同一位置的两次测量值如何保证具有相同的测量起点。
给定一离散周期信号 s(n),从信号 s(n)中两个不同点位开始分别取一个周期的数据,个数为 N。两次采样点序列记为 f(n),g(n),其中 g(n)=f(n+p),其中 p 为两信号的相移点数。则问题归化为已知 f(n),g(n),求两个离散信号序列的相移点数 p。
对 f(n),g(n)做傅里叶变换得


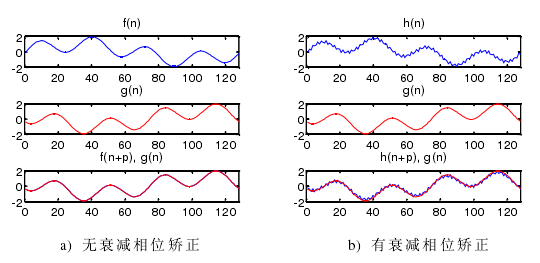
图 4-6 相位矫正
4.2.3 倾角运动误差分离实验数据处理
倾角误差分离试验将按两步进行,首先要到的是被测试件在两个截面内的圆度误差。通过对每个截面内三个传感器采集的数据进行处理,得到被测试件在此截面内的圆度误差信号。此时需要关注的是被测试件每个点位上实际值,后续双截面同时处理时要用到这些具体值。
第一步操作如下:
这里不再赘述单截面主轴径向运动误差和被测试件的圆度误差,下面直接给出被测试件两个截面分别进行三点法误差分离试验的数据结果。表 5-1和图 4-7 给出两个截面测量数据的最小二乘评价表和实际数据的极坐标图。
表 5-1 两截面分别测量得出的圆度误差和径向运动误差

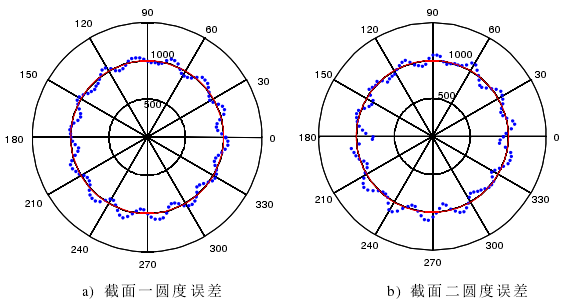
图 4-7 双截面分离出的圆度误差(矫正前)
虽然通过这一步已经分离出主轴在两个截面内主轴的径向运动误差,但是我们不能用这两个截面在这一步测得的数据来求解主轴倾角运动误差。原因有二:第一,这两个截面的三点法频域误差分离试验是分开进行的,也就是说两截面的径向运动误差不是同时得到的;第二,本试验所采用的超精密车床主轴电机编码器不是绝对式编码器,即便不考虑原因一,径向运动误差图也存在相位移动。这些问题将通过第二步来解决。
第二步操作如下:
四个位移传感器分别安装在被测试件的两个截面内 x,y 方向上,对主轴运动进行同时测量。我们已知从每个传感器采集数据中提取的同步运动误差信号中只包含被测试件的圆度误差信号和主轴在此方向上的径向运动误差。而经过第一步试验的处理我们已知被测试件两截面的圆度误差值,此时从任何一个传感器的同步运动误差信号中减掉被测试件对应点位的圆度误差值就会得到主轴在此传感器方向上的径向运动误差值。
四个传感器同时测量可以解决第一步两截面径向运动误差非同时测量的问题,鉴于试验用超精密车床主轴电机编码器不是绝对编码器,另一个需要解决的问题是同一位置处的传感器的两次测量数据中相位匹配,此处的相位匹配是指测量点位的匹配对应,用软件匹配的方法解决硬件编码器在此次测量试验中带来的困难。
主轴电机转速为 1000 r/min,传感器采样频率设为 25600 Hz。主轴每旋转一周采样 1536 点,主轴转动角度分辨率为 0.2344°,相当于每转分度 1536线的编码器。在同一位置处(传感器的位置,而不是测试件的测点的位置)的传感器两次分别测量 20 转数据,从两次测量数据中提取的同步运动误差信号分别记为S1和S2 。因为没有绝对编码器,所以每次测量不能保证相同的起始测点。S1 和S2会在相位上出现偏差,如图 4-8 a),利用算法矫正过的图形如图 b)。
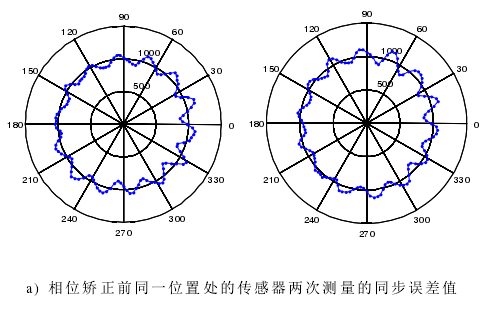
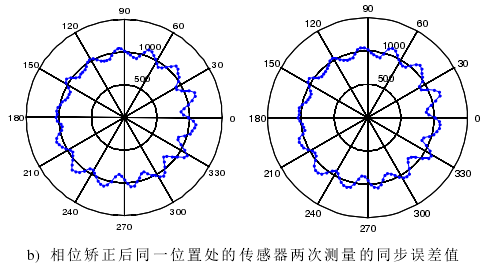
至此,我们已经解决无绝对编码器带来的相位捕捉问题。主轴旋转时对被测试件相同位置处的两次测量数据经过相位矫正后可以保证测量点位从同一点开始采集。从图 4-8 b)可以看出相位矫正效果是很好的。
将第一步和第二步传感器信号进行相位矫正后,从两个截面 x,y 方向上的传感器的同步运动误差中减掉第一步的分离出的圆度误差即可得到两个截面的径向运动误差,如图 4-9 所示。
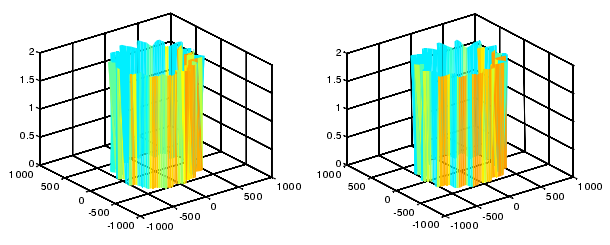
图 4-9 左侧图为两截面 x 轴方向运动误差,右侧图为两截面 y 轴方向运动误差
根据公式(4-8),可计算出主轴在 x 轴和 y 轴方向上的倾角运动误差,如图 4-10 所示。
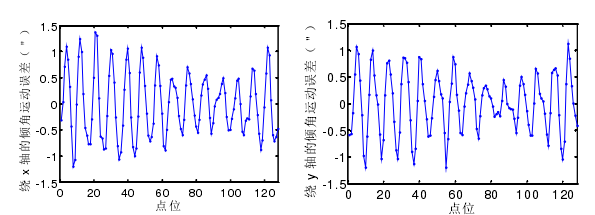
图 4-10 绕 x 轴和 y 轴的倾角运动误差
4.2.4 主轴转速对倾角运动误差的影响
上节分析的是转速在 1000 r/min 时,主轴绕 x 轴和 y 轴的倾角运动误差的分离过程。为研究主轴转速对倾角运动误差的影响,试验还对主轴转速在600 r/min 和 200 r/min 时进行倾角运动误差的分离运动,试验结果如图 4-11。
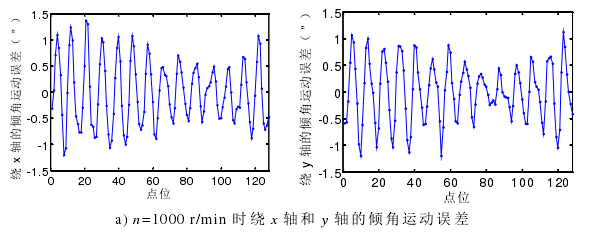
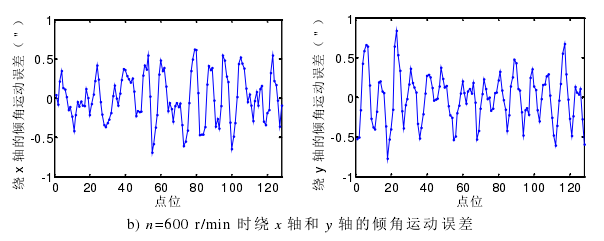
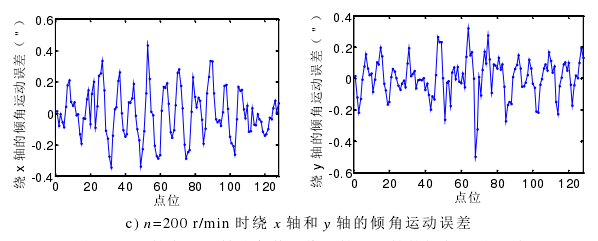
图 4-11 主轴在不同转速条件下绕 x 轴和 y 轴的倾角运动误差
从图 4-11 可知,随着主轴转速的降低,倾角运动误差随之减小。综合之前分析的主轴的径向回转运动误差随主轴转速的降低而减小,可知主轴的在 1000 r/min 以内转动,转速越低,其转动稳定性越好。
4.3 本章小结
本章主要分析双截面测量实验数据在去掉直流分量后,是处在同一个坐标系——绝对坐标系中的,为倾角运动误差的计算提供有效数据;在径向运动误差的基础上推导倾角运动误差求解算法;进行超精密车床主轴倾角运动误差实际测量实验,并对不同转速下主轴倾角误差运动进行研究。
结论
超精密主轴回转误差是影响加工工件表面质量的最主要因素,研究超精密主轴回转误差对于评价主轴回转精度,监测诊断主轴运行故障,预测机床加工工件表面形状误差,加工误差补偿及提高机床加工精度等有重要意义。本文以三点法频域误差分离技术为基础,以超精密车床主轴为研究对象,研究主轴的径向运动误差和倾角运动误差的分离。结论如下:
(1)从传感器测量值实际数学模型的解析构成角度证明最小二乘偏心运动对主轴径向误差运动的不可分离性。给出实际测量环境下传感器安装角位置偏差和安装线偏差对误差分离精度的定量分析,为超精密车床主轴回转误差纳米级测量采集数据的可靠性提高理论保证。
(2)在频域中对除噪、滤波、同步运动误差的提取以及三点法算法的前半部分进行连续性处理,减少测量信号在时域频域中的变换计算。从超精密车床加工工件表面成形角度分析去除一阶谐波分量的依据。
(3)实际测出超精密车床主轴径向运动误差,并根据推导出的主轴倾角运动误差分离算法,测得超精密车床主轴倾角误差。
本文搭建的超精密车床主轴回转误差测试系统还存在一定的问题。虽然摒弃了安装标准件到主轴上进行测量的方案,采用超精密车床自身加工高精度测试件在无拆卸状态下直接进行测量,依然不能很好地解决最小二乘偏心运动对主轴回转误差的影响。在今后的工作中,将重点解决一下几个问题:
(1)主轴径向运动误差的一阶谐波分量与被测截面最小二乘偏心运动量的分离。一阶谐波分量的分离同样影响到倾角运动误差的分离,所以此问题需待解决。
(2)主轴回转误差是影响超精密车床加工对称回转体和快刀加工非对称回转体的表面质量最主要的因素,所以回转误差的加工补偿也是后续工作的重点。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多本专题新闻
专题点击前十
| 更多










