航空整体叶轮五轴数控加工仿真及参数优化研究 (下)
2016-11-21 来源:天津职业技术师范大学 作者: 卢辉
第 5 章 基于动力学仿真的切削参数优化
5.1 概述
航空整体式叶轮约70%的余料需要切除,因此如何合理选择切削参数高效地去除余料是整体叶轮数控加工中提高生产效率的一个瓶颈问题。切削参数直接关系到零件的加工质量,刀具的寿命,生产成本。而在实际生产加工中,切削参数往往是数控工艺人员根据刀具厂商推荐或凭经验来选取的。由此产生的直接后果是:一方面,由于缺乏理论依据,所选择的切削参数过于保守,导致切削效率低下难以充分发挥数控机床,特别是高速数控机床的效能,造成浪费;另一方面,即使以较低的材料去除率进行切削,如果选择的切削参数不合理,也会因颤振的发生而导致零件尺寸超差甚至对机床和刀具本身造成损害。因此,合理地选择切削参数是实际加工生产的迫切需求。本文将在上一章得到的颤振稳定域的基础上,进行切削参数的优化。首先基于最短切削时间对切削参数进行正交试验设计,分析正交试验结果,得出最短切削时间的切削参数。然后基于动力学仿真进行切削参数的优化,最终得到最佳切削参数。
5.2 基于颤振稳定域的切削参数优化
5.2.1 正交试验方法
正交试验是日本田口玄一在上个世纪40年代设计出来的[60]。正交试验是在全面实验中挑选有代表性的样点进行来做实验,这大大减少了实验次数,因而在世界范围内得到广泛应用[61]。正交试验设计是运用数理统计的知识,选取典型的有代表性的样点进行实验,对实验结果进行极差分析和方差分析,找出最佳实验方案。这种方法主要用于优化多因素多水平的科学实验,能够减少实验次数,缩短实验周期,降低实验成本。

5.2.2 正交试验设计
切削加工过程中,在保证加工质量的前提下,提高加工效率,即在稳定的切削的前提下,保证材料的最大去除率[63]。对铣削而言,材料去除率 MRR可表示为轴向切削深度 ap径向切削宽度ae、主轴转速n、每齿进给量f N及铣刀齿数N的函数。
为了在较少的实验次数下充分考虑切削宽度、切削深度、主轴转速、每次进给量对切削时间的影响,本实验将采用正交试验法。在本实验中,切削时间为实验的指标,切削宽度、切削深度、主轴转速、每次进给量为影响因素。根据上一章得出的稳定叶瓣图,每个因素选取4个水平。根据加工经验,将切削宽度选取为3mm,4mm,5mm。由切削宽度为3mm,切削宽度为4mm,切削宽度为5mm仿真得出颤振稳定域分析解如图5-1所示。
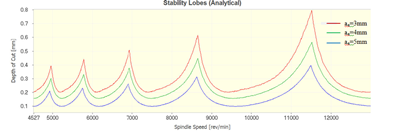
图 5-1 颤振稳定域
从图中可以看出,随着切削宽度的增加,颤振稳定域的切削深度降低。这就会影响正交实验的设计,如果把正交实验设计为四因素四水平的话,有很多组实验因为超出颤振稳定域的切削深度而没有办进行。所以为了更好地选取出最佳的切削参数,把切削宽度不同的情况,单独做正交实验。就是将正交实验设计成切削宽度为3mm,切削宽度为4mm,切削宽度为5mm三组三因素四水平的正交试验。首先,先设计切削宽度为3mm的正交试验,正交试验的因素水平表如下表5-1所示。
表5-1 因素与水平表

5.2.3 参数优化结果及分析
根据因素水平表中的因素和水平,选用正交表L 4 ,如表5-2所示。通过VERICUT软件几何仿真,可以得到每组参数的切削时间。
表5-2 用正交表安排实验
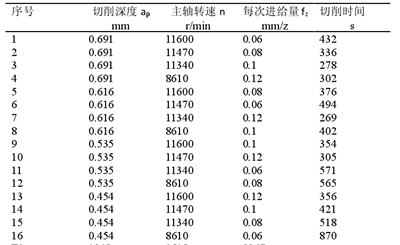
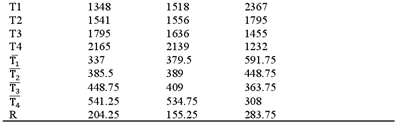
从表5-2中的16次试验结果看出,第7号试验ap=0.616, n=11340, fz=0.12的切削时间最短,为269s。从正交试验结果来看,第7号试验是最佳切削参数方案,当由于正交试验只是在全面实验中做了16组试验,最佳切削参数不一定在这16组试验中,因此为了找出最佳方案,还需要对正交试验结果进一步分析。表5-2中T1、T2、T3、T4这四行分别是各因素同一水平结果之和。例如,ap因素T1行列的数据1348是ap因素4个1水平实验值的和,而ap因素4个1水平分别在第1,2,3,4号试验,所以ap的T1=432+336+278+302=1348。ap因素的T2、T3、T4如下:
T2=376+494+269+402=1541
T3=354+305+571+565=1795
T4=356+421+518+870=2165
同理n因素的T1、T2、T3、T4为
T1=432+376+354+356=1518
T2=336+494+305+421=1556
T3=278+269+571+518=1636
T4=302+402+565+870=2139
同理fz因素的T1、T2、T3、T4为
T1=432+494+571+870=2367
T2=336+376+565+518=1795
T3=278+402+354+421=1455
T4=302+269+305+356=1232




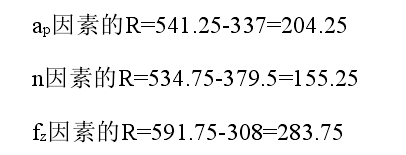
最后分析结果,分析表明极差越大的因素重要程度越高。因此,因素主次顺序应为:n→ap→fz。为了直观起见,用因素的水平变化为横坐标,切削时间的平均值为纵坐标,画出水平与切削时间关系图,如图5-2所示
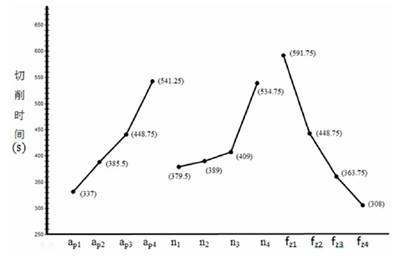
图 5-2 水平与切削时间关系图
从上图可以明显看出,最佳方案是ap1,n1,fz4而正交实验选出的最佳方案是ap2,n3,fz4。显然,正交实验中的16组试验没有ap1,n1,fz4这一方案。其是否是最佳实验还需要验证。通过对颤振稳定域图分析发现,当ap=0.691, n=11600, fz=0.12时,已经超出颤振稳定域的范围,如图所示,说明使用这组参数进行加工时刀具会发生颤振,不是最佳方案。故当ae=3mm时,最佳的切削参数为ap=0.616, n=11340, fz=0.12。
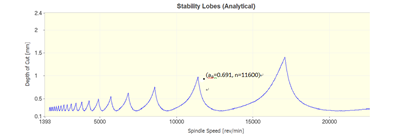
图 5-3 水平与切削时间关系图
在前面进行的极差分析可以得到各因素对切削时间影响的程度,根据各因素影响切削时间最大的水平数得到最佳切削参数。极差分析计算方便,简单易懂,因此得到广泛应用。但是极差分析不考虑实验误差,任何实验中都不可避免出现误差,无法判断有误差引起的数据波动。为了解决这个问题,在正交试验中引入方差分析。 方差分析是通过离方差平方和分解,构造F统计量,生成方差分析表,对因素效应和交互效应的显著性作检查[65]。方差分析可以估计试验误差并对其分析,给出所得结论的置信度区间,对各因素进行显著性分析。进行方差分析的基本步骤:1)试验数据总的偏差平方和SST;2)因素的偏差平方和;3)误差平均方和SSE;4)自由度DF;5)均方MS;6)F值;7)显著性概率P值;
(1)试验数据总的偏差平方和SST
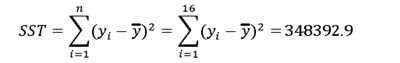
其中n是正交试验的总实验次数,正交表的每一行代表每一次试验得到的实验数据,共有n个实验数据,记为y ,y ,……,y ,本例n=16。y是n个实验数据的平均值。
(2)因素的偏差平方和。设切削深度、主轴转速、每齿进给量的偏差平方和分别为SS1、SS2、SS3。各因素的偏差平方和为:
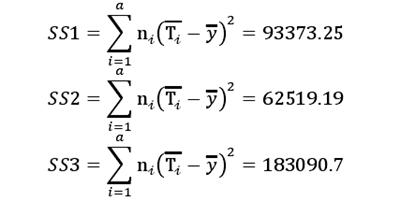
(3)误差平均方和SSE。计算误差平方和,不考虑交互作用的一般公式:
(4)自由度DF。在正交设计中,各列的自由度是水平数减1,总自由度是实验次数减1,即
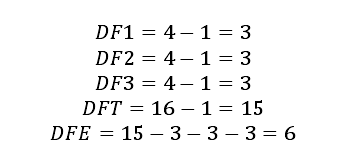
(5)均方MS。均方就是偏差平方和除以自由度,即

(6)F值。因素的均方和误差均方差的比值F是一个统计量,即
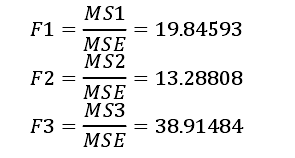
(7)显著性概率P值。P值可以确定两个数据集是否存在变化程度上的不同。借助Excel表软件来计算p值。即

从P值的结果来分析,可以看出每齿进给量的显著性最高,其次是切削深度,最后是主轴转速,说明每齿进给量对切削时间影响最大,其次是切削深度,最后是主轴转速。这与前面用极差分析是一致的。 前面讨论的是当ae=3mm时候的情况,下面来讨论ae=4mm,ae=5mm的最优切削参数,根据稳定叶瓣图选取表5-3、表5-4的切削参数。
表5-3 ae=4mm的因素与水平表

表 5-4 ae=5mm 的因素与水平表

同理对表5-3、表5-4做正交试验得出,当ae=4mm时,最佳的切削参数为ap=0.475, n=11340, fz=0.12,切削时间为326s;当ae=5mm时,最佳的切削参数为ap=0.375, n=11340, fz=0.12,切削时间为450s。而当ae=3mm,ap=0.616, n=11340, fz=0.12时,切削时间为269s。从正交试验得出的最少切削时间的加工参数是ae=3mm,ap=0.616, n=11340, fz=0.12,但实际加工中还需考虑机床的主轴功率、切削力、主轴扭矩等情况。因此,使用Cutpro9.0软件对这三组参数进行切削过程的仿真,预测切削时的主轴功率、切削力、主轴扭矩、表面粗糙度等。
5.3 基于动力学仿真的切削参数优化
5.3.1 Cutpro9.0的动力学仿真功能
在切削过程仿真模块中,通过设定刀具几何形状、加工参数、工件和刀具的动态模态参数可以模拟出X、Y、Z方向的切削力和切向切削力、在XY平面上的切削合力、切削厚度变化情况、刀具振动、工件振动、由于强迫振动和颤振引起的表面光洁度、主轴的功率和扭矩、作用于刀具上的弯矩、切削动画等。 切削过程仿真对非线性效应比如刀具走空刀、刀具跳动、复杂的刀具几何形状等进行详细检查非常有用。切削过程仿真可以预测在考虑刀具和工件结构动态下的切削力,看看切削力是否超过机床所能承受的范围;可以检查颤振的情况,如果颤振非常激烈的,很容易导致刀具的折断;可以预测切削过程中的主轴功率和扭矩,看是否超出机床最大主轴功率和扭矩的范围;通过近似的切屑模型或形成切屑的精确运动,可以预测切削厚度变化情况;可以显示刀具和工件在X、Y方向振动情况;通过观察表面光洁度图,可以预测表面光洁度的粗糙度值,看看它是否在可接受的公差内。 5.3.2 动力学仿真结果及分析 在进行切削过程仿真之前,使用Modal(模态分析模块)通过对锤击实验获得的频响函数(FRF)进行辨识处理,得到包括固有频率、阻尼比和刚度在内的模态参数曲线。首先点击“NEW Analysis”,在弹出的对话框中选择锤击实验获得的频响函数文件,选择想要的模态参数,点击刷新按钮,选中的模态参数将拟合成模态参数曲线,点击保存为.cmp格式文件。如图5-4、图5-5分别是D6平底铣刀X方向、Y方向的模态参数曲线。
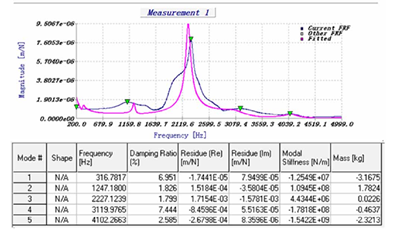
图 5-4 X 方向的模态参数曲线
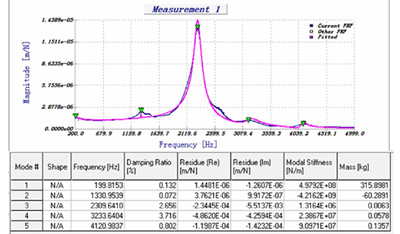
图 5-5 Y 方向的模态参数曲线
图5-4和图5-5中,蓝色的曲线是锤击试验获得的频响函数,粉色的曲线是模态参数曲线,五个绿色的三角符号是选中的模态参数,从左到右分别对应表格中的一阶模态参数,二阶模态参数,三阶模态参数,四阶模态参数,五阶模态参数。这些参数包括了固有频率、阻尼比和模态刚度在内等参数。得到模态参数曲线后,下面进行切削过程的仿真。为了叙述方便,本文将ae=3,ap=0.616, n=11340, fz=0.12设为A参数,ae=4,ap=0.475, n=11340, fz=0.12设为B参数,ae=5,ap=0.375, n=11340, fz=0.12设为B参数。仿真具体操作步骤就不再这叙述了,通过切削仿真后得到切削参数的主轴功率、切削力、主轴扭矩、刀具振动。为了减少篇幅,本文列出A组仿真结果图进行分析。图5-6至5-10为A组切削参数仿真结果。
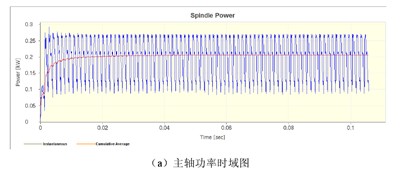
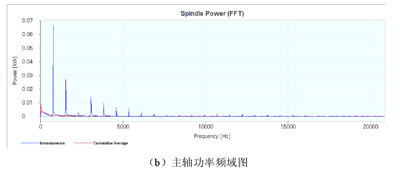
图5-6 主轴功率仿真结果
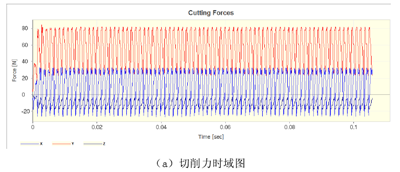
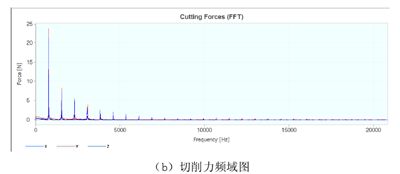
图5-7 切削力
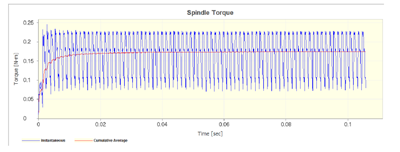
图5-8 主轴弯矩时域图
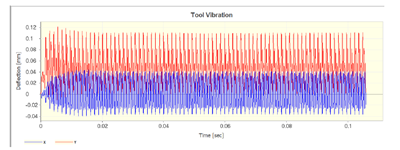
图5-9 刀具振动时域图
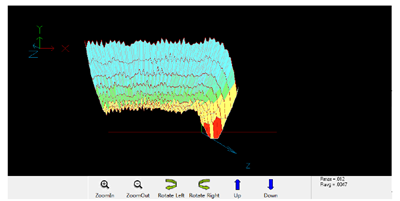
图5-10 表面粗糙度
将立铣的进给方向和进给方向的法向分别定为笛卡尔坐标系的X和Y轴,Y轴方向的任何偏差将产生静态形状误差。螺旋立铣刀产生的形状误差相当复杂[66]。如图5-7(a)切削力时域图所示,切削力并非常数,因为立铣刀是螺旋刃的,切削力是随立铣刀的旋转变化的,另外,由于螺旋槽的螺旋角的存在,也将产生沿着刀具Z轴变化的切削力[67]。因为切削力不是常数,所以主轴功率和主轴弯矩也是瞬时变化的,如图5-6和5-8所示。顺铣加工中,切削厚度是由大变小的,切削力在刚切入工件时达到最大,随着切削刃切出离开工件,切削力逐渐减小。从图5-7(b)切削力频域图可以看出切削力是符合顺铣加工周期性变化规律的,这也说明切削是稳定的没有发生颤振。如图5-9所示,刀具振动呈现出周期性变化,并没有发现异常,说明切削过程没有发生颤振。图5-10是加工表面的光洁度,看到最大值为0.012,平均值为0.0047,满足工件加工要求。其他两组的仿真结果如表5-4所示。
表5-4 仿真结果

从表中的仿真结果可以看出,三组切削参数的主轴功率、切削力、主轴弯矩、刀具振动差别不大,A组的表面粗糙度值与B组和C组的表面粗糙度值相差很大。由前面的正交试验可知,A组的切削参数是切削时间最短的。所以综合考虑本文选取A组参数进行加工。
5.4 本章小结
为了在较少的实验次数下充分考虑切削宽度、切削深度、主轴转速、每次进给量对切削时间的影响,本节将采用正交试验法。首先在工艺系统颤振稳定域仿真的基础上,以切削时间为优化目标,切削深度、主轴转速、每齿进给量为实验因素,设计三因素四水平的正交试验,通过几何仿真获得切削时间。然后对实验结果进行直观分析和方差分析,得出各组的最佳切削参数。为了更好地选择切削参数,实际加工中还需考虑机床的主轴功率、切削力、主轴扭矩等情况。因此,使用Cutpro9.0软件对这三组参数进行切削过程的仿真,预测切削时的主轴功率、切削力、主轴扭矩、表面粗糙度,最终得出ae=3mm,ap=0.616, n=11340, fz=0.12为最佳切削参数。
第 6 章 叶轮五轴数控加工实验验证
本章将进行叶轮的实际加工验证前面优化的粗加工参数,为了充分地验证优化结果将选取两组前面优化后的切削参数进行叶轮试切加工。第一组粗加工参数为ae=3,ap=0.691, n=11600, fz=0.12。第二组粗加工参数ae=3,ap=0.616, n=11340, fz=0.12。为了叙述方便,本文将第一组参数加工的叶片称为第一组叶片,将第二组参数加工的叶片为第二组叶片。
6.1 实验准备
6.1.1 叶轮毛坯的准备
本文研究的航空整体叶轮总高度为57.1mm,直径为Φ123.2mm,如图6-1所示。结合实验室的实际情况,将采用三爪卡盘进行装夹。为了避免加工中主轴与工作台的碰撞,将叶轮的毛坯定为直径为Φ130mm,高度为160mm的棒料。首先使用数控车进行加工棒料得到叶轮的毛坯,使用三爪卡盘装夹在机床上如图6-2所示。
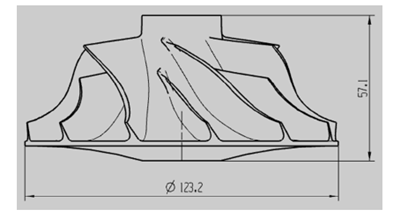
图6-1 叶轮的整体尺寸

图6-2 叶轮的装夹方案
6.1.2 叶轮数控程序的编制
为了提高叶轮的加工效率,本文选择3+2定轴加工方法进行叶轮的粗加工。创建叶轮粗加工的操作过程:首先定义加工坐标系、加工毛坯,创建加工刀具,打开型腔铣加工策略,按照前面优化出来的加工参数进行设置,切削宽度为3mm,切削深度为0.616mm,主轴转速为11340r/min,每齿进给量为0.12 mm/z,生成如图6-3的叶轮粗加工刀具轨迹。同理设置另一组参数的粗加工和精加工刀具轨迹。
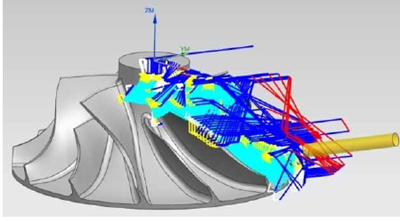
图6-3 叶轮加工刀具轨迹
6.2 实验结果分析
将编制好的数控程序传输到五轴机床,装夹刀具,设置工件坐标系,开始加工叶轮。加工过程中主要观察刀具是否与夹具等发生干涉。加工过程如图,通过观察加工过程,发现刀具与夹具,主轴与工作台等并没有发生干涉,与上一章VERICUT仿真结果一样。这说明本文构建的VERICUT能够准确检查机床干涉问题。如图6-4所示第一组切削参数得到的粗加工结果,和使用第二组切削参数粗加工后的零件。


图6-4 叶轮粗加工
第一组参数的切削时间为10min,第二参数的切削时间为15min。实际的切削时间和前面预测的切削结果一样。下面进行叶轮精加工。为了叙述方便,本文将第一组精加工得到的图6-5是两组精加工后得到的叶


图6-5 精加工后的叶片
从图6-5中发现,第一组叶片的背面在精加工完之后还残留粗加工的刀痕,说明第一组叶片粗加工阶段发生过切现象,第二组叶片的背面是精加工完成后得到光洁的表面,说明第二组叶片粗加工时没有发生过切情况。这是因为第一组切削参数的进给速度太快,而叶片与叶片间的流道狭窄,机床运动轴速度过快而导致过切。两组的叶片正面都没有发生粗加工过切现象。
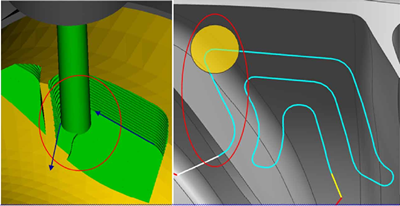
图6-6 叶片过切处刀路轨迹
通过VERICUT仿真查看过叶片过切处的情况,如图6-6所示,在红色圈内是叶片发生过切处的刀路轨迹,蓝色箭头是刀具的走刀方向。从图中可以看到刀具是从右向左切削,经过一个角度为锐角的拐角。而第一组的进给速度为5443mm/min,快速通过拐角位置时,由于速度越快刀具受到的离心力越大,同时拐角的角度为锐角,导致刀具变向急剧,从而导致过切现象。而第二组的进给速度为2000 mm/min,切削经过拐角处的速度比较慢,受到的离心力小,因而叶片没有发生过切现象。
6.3 本章小结
本节使用两组前面优化的切削参数,进行叶轮的切削加工。通过观察切削过程,并没有发现机床主轴与夹具、工作台等发生干涉,从而验证了本文建立的VERICUT数控仿真环境是可行的。叶轮加工完成后,得到第一组粗加工的切削时间比第二组粗加工切削时间短,但是第一组的粗加工发生了过切现象,第二组粗加工没有发生过切情况。这与前面切削参数优化分析结果一致。
第 7 章 结论与展望
7.1 结论
本文以航空整体叶轮为研究对象,首先获取叶轮加工的颤振稳定域,然后基于动力学仿真进行切削参数优化。最后在VERICUT软件中建立叶轮加工仿真环境,并进行实验验证优化后的切削参数和建立的叶轮仿真环境。得出以下结论:
1.在 VERICUT环境下建立虚拟的数控机床实体、控制系统、刀库、坐标系统等,创建数控仿真环境,实现针对具体工艺系统的几何仿真,同时,总结出几点利用VERICUT软件进行虚拟数控机床建模的关键技术。通过实验验证VERICUT数控仿真环境有效检查机床主轴、刀具与工作台、夹具之间碰撞。
2.针对海德汉i TNC530数控系统的倾斜加工面功能,通过对CLSF刀位轨迹进行齐次变换运算,提出了机床运动坐标的数控程序后处理算法。使用UG NX8.5/Post Builder编写后处理文件。通过实例验证表明该后处理算法能够实现在倾斜面加工上输出圆弧插补,大大提高叶轮加工效率。
3.采用力传感器和加速度传感器,通过锤击实验来获取机床-刀具和机床-工件的频响函数。然后采用Cutpro9.0的动力学仿真功能,在给定的径向切削深度(切宽)条件下,进行颤振稳定域仿真,获得表征主轴转速和轴向切深关系稳定域叶瓣图,为后续几何仿真和动力学仿真的切削参数优化奠定基础。
4.在工艺系统颤振稳定域的基础上,以切削时间为优化目标,切削深度、主轴转速、每齿进给量为实验因素,设计三因素四水平的正交试验,通过几何仿真获得切削时间。根据极差分析和方差分析,得出三组较短切削时间的加工参数。对初步优化得到的三组切削参数进一步进行动力学仿真,根据仿真结果确定最优工艺参数。通过叶轮实际切削加工发现,优化后的加工参数能够缩短加工时间,且不发生颤振。
7.2 展望
本文对航空整体叶轮进行五轴数控加工仿真及参数优化研究。由于叶轮加工仿真及参数优化涉及学科广泛,本文只是做了一些初步研究,仍有很多不足。有待进一步研究的几个方面:
1.本文研究的叶轮流道比较狭窄,刀具轨迹的直线段距离比较短,实际加工中机床运动轴频频减速加速或突然变向,未能考虑运动轴在加速减速或突然变向给机床带来额外的振动。
2.本文主要研究了立铣刀定轴加工叶轮的情况,没有对球头铣刀五轴联动加工叶轮这种情况做研究,而且本文主要考虑了机床-刀具的动态特性,没有考虑到机床-工件的动态特性。
3.今后的研究,应该在优化五轴机床的刀具轨迹和刀轴干涉的基础上,以最小表面粗糙度为目的优化切削参数。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多本专题新闻
专题点击前十
| 更多










