0 引言

      随着汽车、船舶工业的迅速发展，对发动机性能的要求越来越高，活塞作为发动机的“心脏”，其质量的好坏直接影响着发动机的工作性能。目前椭圆型面的活塞被广泛应用，即活塞横截面为椭圆或近似椭圆，由于椭圆活塞独特的结构特点，椭圆活塞的动力性能和润滑性优于普通活塞，能在发动机内恶劣的环境下承受复杂的机械负荷和热负。国内一些高校和企业都在研究椭圆活塞的加工技术，如一些高校研究采用车削技术加工椭圆活，一些机械企业使用X-Y跟踪方法来磨削椭圆活塞等，当前较多采用X-C两轴联动的磨削方法加工椭圆活塞，即C轴带动工件转动的同时X轴跟随廓形曲面做往复运动，联动磨削方法无论是误差控制还是表面质量上都有明显的优势。

      1 椭圆活塞联动磨削加工机理

      椭圆活塞是典型的非圆回转零件，椭圆活塞磨削的研究思路如图1所示，椭圆活塞的截面廓形是磨床的X轴（砂轮横向进给轴）与C轴（零件回转轴）联动生成轨迹的结果。要进行椭圆活塞磨削，首先从活塞的非圆轮廓的廓形特征入手，根据给定的廓形参数推算出磨削算法公式，利用Matlab工具算出加工坐标，即C轴转动角度与X轴进给距离的对应关系。

      为了保证椭圆活塞轮廓曲面的磨削精度和表面质量，理想状态是采用恒磨除率来进行磨削，

      以保证磨削力的恒定。通常恒线速度法是保证横磨削率的方法之一，若采用理想状态的恒线速度磨削会使得C轴转速波动很剧烈，尤其在廓形变化较大处，往往会由于头架转速过大使砂轮架跟踪不到位产生较大的跟踪误差。因此，磨削加工需要对得到的恒线速度下的头架转速进行优化。

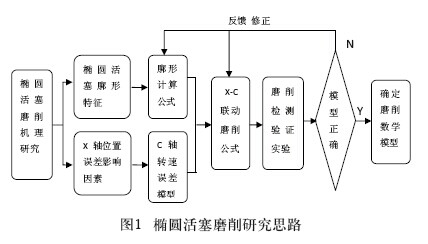
      由于椭圆活塞曲面磨削机理的复杂性和不确定性，以及曲面结构的刚性差，加之数控系统本身对磨削精度的影响，按照理论运动轨迹进行磨削无法达到加工的要求，造成廓形误差的出现。系统误差可以通过误差预测，提前制定误差补偿器来控制。加工位置误差和速度误差通过反馈、前馈和交叉控制的综合方法控制。

      2 椭圆活塞的磨削运动模型

      椭圆活塞采用X-C联动磨削，首先根据轮廓的廓形特征写出椭圆活塞的直角坐标计算公式，再将实际轮廓上的任一点转化为对应的极坐标系，根据磨削加工数学模型的几何，最后推算出联X-C联动加工坐标公式。椭圆活塞作为一个非圆回转类零件，为了便于计算把椭圆活塞的横截面近似成标准的椭圆形。

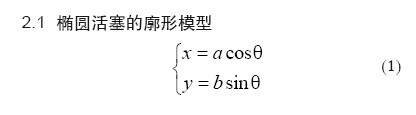
      2.2 椭圆活塞X-C联动磨削的数学模型的建立

      根据椭圆活塞的磨削机理建立的联动磨削加工的数学模型如图2所示。

      由于椭圆活塞几何形状复杂，在磨削过程中波动会比较大，导致加工位置发成错位变化，再加上磨床本身的精度限制，两者相耦合，最终形成廓形误差。

      仿真误差公式为： 

      式中，lAB为砂轮中心到切削点的距离。X-C轴联动数学模型反应了工件旋转运动与砂轮往复运动的联动关系，在加工过程中要求式（4）中的S（X轴砂轮的坐标）与C（工件的转动角度）有一一对应的位置关系，工件每转动一个单位的角度，与之对应的砂轮就移动到相应的位置上，形成所需要的非圆轮廓轨迹。

      3 基于Matlab的磨削过程仿真

      为了验证椭圆活塞磨削的数学模型及联动磨削加工坐标公式的准确性，利用Matlab工具箱设计GUI界面并编写加工程序进行仿真加工。 仿真采用“反转法”方法。反转法的原理为：非圆曲面采用两周联动磨削，其实质是一种砂轮包络的过程，仿真时工件固定不动，砂轮以-围绕工件旋转来对磨削过程进行分析。

      借助Matlab工具，编写一套用反转法仿真非圆廓形磨削加工的程序。 在Matlab中，需要对各个按钮对象进行布局和事件编程，当用户激活相应的GUI对象，就能执行相应的事件行为来实现各种功能。

      3.1 椭圆活塞仿真过程

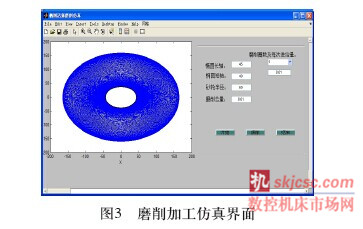
      首先设计仿真的用户界面，利用Mat lab的GUIDE创建GUI界面，在Matlab的菜单栏点击File->New->GUI，或点击快捷图标GUIDE，建立一个新的GUIDE空白模板，设置界面属性，向模板中添加需要的控件组件，如坐标轴、组合框、编辑框、静态文本和按钮控件，按照需要排列布置好各控件的位置，右击控件，选择“PropertyInspector”,设置各个组件的属性，美化仿真界面。

      添加控件的参数变量及编写相应回调函数的程序代码，在需要编写成按钮上右击，选择ViewCallbacks->Callback打开M文件编辑器添加回调函数，在回调函数中编写相应的程序代码。

      “开始”按钮的回调函数：

      function Draw_pushbutton_Callback(hObject,eventdata, handles)

      “清除”按钮的回调函数：

      function pushbutton3_Callback(hObject,eventdata, handles)

      cla;

      部分加工程序代码：

      t=0:pi/180:pi/2

      x=A*cos(t);

      y=B*sin(t);

      dx=diff(x);

      dy=diff(y);

      k=-dx./dy;

      m=atan(k);

      x1=x(1:90)+(R+L-d)*cos(m);

      y1=y(1:90)+(R+L-d)*sin(m);

      x3=x(1:90)+(L-d)*cos(m);

      y3=y(1:90)+(L-d)*sin(m);

      for q=1:90

      h=0:pi/180:pi*2
  

      x2(q,:)=x1(q)+R*cos(h);

      y2(q,:)=y1(q)+R*sin(h);

      end

      3.2 磨削仿真结果

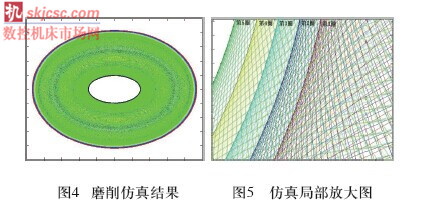
      参数属性设置和加工程序编写完成后，查看属性设置结果，单击菜单栏的“Run”按钮出现仿真磨削界面，如图3所示，在界面中输入各参数：椭圆活塞的廓型参数（长轴、短轴）、砂轮半径、磨削总量、需要磨削圈数和每圈进给量。以磨削五圈为例，点击“开始”按钮，运行加工程序，图4为仿真结果，局部放大图如图5所示。

      4 结论

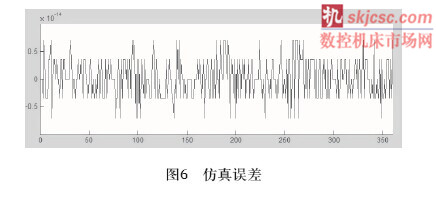
      仿真结果显示椭圆活塞的轮廓表面是平滑的，没有出现传统加工中的上下波动和锯齿形的情况，从图6仿真误差结果看来，误差上下波动在0.8之间，波动非常小，验证了建立的磨削数学模型有效性和磨削算法的准确性，X-C轴联动磨削方法的可行性。与传统加工方式相比，X-C轴联动磨削可提高椭圆活塞的表面质量、加工效率，简化加工工艺，可应用到实际的磨削加工中，同时论文的研究内容对其他非圆回转类零件廓形的磨削也有一定的借鉴和参考价值。