摘要:根据铁路机车轴承的结构特点, 综合考虑滚动轴承座及内外套圈的弯曲变形,本文建立了轴承载荷分布计算模型。通过有限元分析计算, 给出了轴承实际载荷分布值, 并为轴承支座的刚性设计提出了设计要求和建议, 为滚动轴承的CA D 优化设计提供了切实可行的计算方法。

关键词: 计算机辅助设计; 滚动轴承; 载荷分布

      传统的轴承载荷计算, 视轴承支座及内外套圈为刚体, 因而存在着较大的误差. 实际上, 不论是轴承座或者内外套圈都是;弹性体, 受力后都要发生变形. 根据铁路机车轴承的结构特点, 作者综合考虑了滚动轴承座及内外套圈的弯曲变形, 也考虑到滚动物承支座和内外套圈的弹性后的计算是一个接触问题( 包括点接触和面接触) , 过程比较复杂. 为了工程设计中的实用性, 需要寻求一个既能准确反映实际工况, 又便于工程设计的简化的计算模型。

     本文建立的轴承载荷计算模型则反映了这一点, 从而使设计计算结果更加符合实际工况. 通过有限元分析计算, 给出了轴承实际载荷分布图, 并为轴承支座的刚性设计提出了设计要求和建议, 为滚动轴承的C A D 优化设计提供了切实可行的计算方法.

1 计算模型

      铁路机车轴承的实际工作情况如图1 (“) 所示. 为了便于工程应用, 考虑到滚动轴承的内慈外套圈在额定工况下由于受热膨胀等各种因素分别与机车轮轴和轴承座紧配合, 因此作如下假设:

      a. 视内外套圈分别与轴和轴承座为一体.

      b. 对受载滚子的刚度和外圈一支座联合体与滚子接触点的刚度经综合处理( 串联) 后,视为一组弹性支撑, 如图1 (b) 所示.

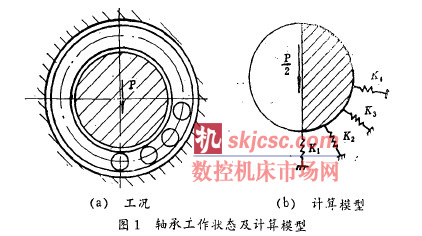
      通过经验公式1和有限元法分别求得滚子的刚度和外圈一支座联合体与滚子接触点的刚度, 并经串联计算得弹性支撑的刚度( K I , K : , K : , K ; ). 图1( a ) 中的P 是轴承的外载荷. 在图1 (b ) 中, 由于考虑平面问题, 载荷需左右对称, 因而载荷取P / 2 .

2 计算方法

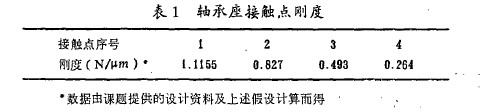
      以滚动轴承4 2 7 2 4.为例进行了载荷分布计算. 对于短圆柱体滚动体, 因载荷在轴向看作均布, 故可作平面问题考虑, 用有限元法求得外圈一支座联合体与滚子接触点处的刚度. 相对于其它弹性体的刚度支座的刚度大得多, 故处理为线性. 4 2 7 2 4 滚动轴承共有14 个圆柱滚子, 受载滚子数最多为7 个, 且左右轴对称. 表1 所列为模型所示4 个接触点的刚度。

      滚子的刚度为非线性, 利用Pa lm gr e n 公式可迭代求得。Pa lm gr e n 公式

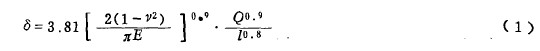
      其中δ 一变形量( m m ) ; E 一弹性模量( N / m m 2 ) ; ,v一泊松比;L一滚子有效接触长度( m m ) ; Q 一滚子上的作用载荷( N ).

      由于公式(1) 中包含了滚子载荷Q , 因而实际的滚子刚度要在总的计算程序中经迭代计算而得.

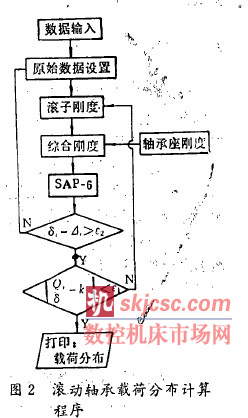
      滚动轴承载荷分布计算程序如图2 所示. 输入的原始数据主要包括轴承的几何参数、轴承的总载荷p、原始游隙△ 等. 初值设定指受载滚子数的设定和滚子刚度的设定. 首先几设’定受载滚子数为7 ( 最大可能受载滚子数), 然后依据判定条件判定; 滚子刚度按公式(1) ,韶魄取平均载荷可得初始刚度. 支撑刚度由滚子的刚度和外圈一支座与滚子接触点的刚度串联计算而得. 至此, 可取用图1 (b) 的计算模型进行有限元计算分析.

      有限元计算程序采用SA P一6. 以内圈一轮轴联合体作为一个弹性体, 支撑刚度( K l , K : , K 3 ,一K ; ) 作为边界条件( 柔性支撑). 由sA P 一6 计算可得边界节点( 弹性支撑点) 处的位移和支反力. 最终求得的各点支反力即为轴承的载荷分布值。

     轴承载荷分布的计算是一个迭代过程. 迭代判定准则如下:

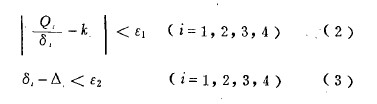
      其中, k 为前一次迭代计算的弹性支撑的刚度;

    ( 1 一cosφ1)表示支承点的原始游隙; 叻: 是支承点的方位夹角;

      经图2 所示计算程序的迭代计算, 最后可得滚动轴承的载荷分布和受载滚子数。

3 计算结果及分析

      以4 2 7 2 4 滚动轴承为例奋设轴承载荷P ＝1000 N /mm ; 原始游隙△＝50μm 协m . 经计算,滚子的载荷如表2 所示。

      本例计算经四次迭代而得, 因而计算方法是可行的. 从表2计算结果可见,.最大载荷在序号2 滚子上, 这与传统的滚子载荷分布计算有较大的差别.常规的计算认为最大载荷是位于序号1 谁子上的, 即认为位于轴承载荷作用线上的滚子承受的载荷最大.这是由于在通常的计算中, 没有考虑轴承内外套圈接触处的接触变形, 并假设其它部分均为刚性的终熬,而本文的计算模型不仅考虑了滚动体与内外套圈的接触变形, 同时还考虑了内外套圈以及轴承座的弯曲变形, 因此, 该计算方法所得的结果能更加真实地反映工程卖际情况;  此外还可以看到, 轴承座的刚性将极大地影响轴承的载荷分布, 进而影响到轴承的使用寿命和相应设备的可靠性. 因此, 只有轴承设计与轴承座设计的统一和协调, 才能使设计更加合理, 从而提高产品的质量。

4 结论

     a.  本文所提出的滚动轴承载荷分布的计算模型和计算方法比传统的设计计算方法更接近实际工况, 具有工程实际应用价值.

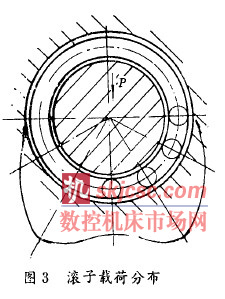
      b . 考虑轴承座和轴承套圈的弹性后, 最大受载滚动体不一定在轴承载荷作用线上. 对所计算的4 2 7 24 轴承, 载荷分布如图3 所示, 这将导致合理的结构设计.

      c.  支座的附性明显影响轴承载荷分布, 因而通过轴承座合理的刚性设计, 可以调正轴承的载荷分布, 使之更加合理.