图像测量是一种采用CCD( 电荷耦合器件) 进行摄像测量的新型光电测量技术, 它是将CCD器件与光学仪器联用, 应用于测量领域而形成的。图像测量技术是以现代光学为基础, 融计算机图像学、信息处理、计算机视觉、光电子学等科学技术为一体的现代测量技术, 它把被测对象的图像当作检测和传递信息的手段, 从中提取有用的信号来获得待测的参数。

     近年, 图像测量技术在国内外发展很快, 已广泛应用于几何量的尺寸测量、航空遥感测量、精密复杂零件微尺寸测量和外观监测、光波干涉图、应力应变场状态分布图等和图像有关的技术领域。本文将图像测量技术用到零件尺寸参数的测量之中,并为了提高测量系统的精度, 提出了一种先在Sobel算子的基础上去掉局部非极大值点获得象素级边缘, 进而在梯度方向上进行高斯曲线拟合插值, 进一步提高图像边缘定位精度, 从而使测量系统精度大大提高的方法。

1 测量系统的构成

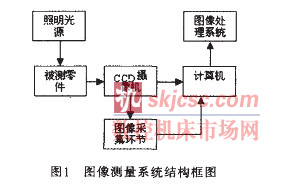
     图像测量系统是集光学、光电子学、精密机械及计算机技术为一体的综合系统。高精度零件尺寸测量系统由CCD摄像机、图像卡、计算机及图像处理软件等组成, 再加上相应的照明系统、接口硬件, 结构框图如图1所示。其工作过程为: 将被测零件置于尽可能均匀照明的可控背景前, CCD和图像卡将被测零件图像采集到计算机里, 计算机按一定的算法计算出被测物体的几何参数, 最后, 计算机对这些数据进行各种处理并将结果按一定的要求予以显示和存储。

2 测量算法

     在图像测量系统中, 图像边缘的检测是整个测量的基础和关键。图像边缘检测精度高, 整个测量系统的精度就可大大提高。零件的轮廓通常产生阶跃型边缘, 因为零件的图像强度不同于背景的图像强度。对于阶跃型边缘的检测, Canny算子边缘检测效果比较好, 但算法复杂;Marr提出用二维高斯加权函数对原始图像作平滑, 然后检测二阶方向导数作为边缘点, 过滤了噪声, 但可能将原有的边缘也给过滤掉了[1] ; 利用Sobel算子检测边缘方法简单, 处理速度快, 得到的边缘光滑、连续。虽然得到的边缘较宽, 但在其梯度图像中去除非局部最大值点, 就可以检测出更精确的边缘。

     为满足图像测量的需要, 本文先在Sobel算子的基础上去掉局部非极大值点获得象素级边缘, 进而在梯度方向上进行高斯曲线拟合插值, 进一步提高图像边缘定位精度到亚象素级, 从而大大提高测量系统的精度。

     2.1 象素级边缘提取

     象素级边缘提取是指用象素级的边缘检测算子对目标初步定位, 得到象素级精度的定位过程。本文利用Sobel算子, 在梯度方向上去除非局部最大值点, 成功地获得了象素级边缘, 取得了较好的效果。具体的步骤如下。

     ( 1) 用Sobel算子对去噪后的图像g( i, j) 进行卷积, 得到卷积图像。

     ( 2) 计算图像中每一点的梯度方向值θ, 其计算公式为: θ( i, j) =tan- 1( f ′y / f ′x) , 这样就可以得到图像中每一点的梯度方向值。根据离散数字图像的特点, 将θ分成四个方向范围: 0( 水平方向) : 0°—22.5°以及157.5°—180°; 45( 45方向) : 22.5°—67.5°; 90( 竖直方向) : 67.5°—112.5°; 135 ( 135 方向) : 112.5°—157.5°。

     ( 3) 对梯度图像中的所有边缘点, 在每一点的3×3邻域中, 将中心象素梯度值与沿梯度方向的两个象素梯度值进行比较, 若在邻域中心处的幅值比沿梯度方向上的两个相邻点的幅值大, 则此点为边缘点, 否则, 此点为非边缘点, 赋值为0, 从而得到单象素边缘图像。

     图2是利用Sobel算子在改进前后得到的微孔零件图像的边缘图。从图2中对比结果可以看出, 经典Sobel算子获得的图像边缘比较宽, 而利用改进的算子获得的图像边缘较细, 达到了单象素级水平, 取得了比较满意的效果。

     2.2 亚象素边缘定位

     图像边缘可以精确到一个象素点, 这样, 边缘点坐标可以近似地为像元的几何中心位置。这时系统的测量精度由CCD感光部分的像敏元间距决定。因此, 图像测量系统的测量精度, 在不考虑像差等因素的情况下, 主要取决于CCD摄像机的分辨率。为了提高测量系统的精度, 提出了一种概率统计细分方法来提高CCD尺寸测量分辨率, 提出了解调测量方法来提高CCD尺寸测量分辨率, 提出应用概率论方法来提高CCD尺寸测量分辨率, 提出应用多项式插值函数来提高CCD尺寸测量分辨率等等。本文提出在梯度方向上进行高斯曲线拟合插值进一步提高图像边缘定位的精度, 从而使测量系统的精度大大提高的方法。

     2.2.1 高斯曲线拟合原理分析

     在图像边缘梯度方向上, 灰度梯度呈一个高斯曲线分布。若用边缘检测算子直接提取图像边缘, 则只需找出灰度变化最大的象素的坐标就可以了。但是, 灰度变化最大的象素坐标不一定是这个高斯曲线的极值点, 而且可以说往往不是极值点, 如图3所示, 我们往往认为0位置点就是图像的边缘点, 但从图中可以很明显地看出来, 实际的边缘位置点不是0点, 而是xg点。对于一个图像测量系统来说, 若认定0位置点就是我们所要找的边缘点, 这往往达不到系统测量的精度。为了提高系统测量的精度, 必须找到xg点的准确位置, 这可以通过采用亚象素细分算法来精确定位xg点。在图3中, 0点的梯度值最大设为F0, - 1点和1点的是在梯度方向上紧挨0点的左右两点, 设它们的梯度值分别为F- 1和F1, 通过这三个梯度值拟合出一条高斯曲线, 然后通过求导来取得其极值点, 则对应极值点的坐标点xg即为图像边缘的精确定位点。

     2.2.2 梯度方向上高斯曲线拟合插值细分算法

      通过Sobel算子可以很方便地得到每个边缘象素点的梯度值和梯度方向值, 根据这两个值就能够进行下一步梯度方向上的高斯曲线拟合。高斯曲线的表达式为其中u为均值, σ为标准差。直接对此式进行拟

合很困难, 可以把高斯曲线作变换, 两边取对数, 有下式成立

     可以看出上式形如y=Ax2+Bx+C, 是一条典型对x的二次曲线。这样就能用取对数后的值来拟合出抛物线, 求出顶点坐标, 使计算大大简化。

     为了求出梯度方向上二次曲线的形式, 我们采用曲面拟合的观念: 先用一个二元二次多项式去拟合边缘点附近邻域内象素梯度的对数值, 得到曲面拟合函数, 然后再通过曲面拟合函数来得到二次曲线形式。通常, 我们利用边缘点附近3×3邻域象素点来计算参数, 当然也可以加大区域取点范围, 这样求出的曲面函数效果也比较好。但是, 这会增加检测时计算的复杂度, 且增加的效果不是很明显。所以我们通常采用边缘点附近3×3邻域象素点来计算参数。

     设曲面拟合函数为:

                         f( x, y) =k0+k1x+k2y+k3x2+k4xy+k5y2 ( 2)

     其中的x, y为象素点的坐标值, f( x, y) 为在象素点( x, y) 处梯度大小的对数值。所以, 关键是计算方程( 2)中曲面拟合函数的系数, 可用最小二乘法求出系数k0, k1, ⋯, k5的值, 然后运用公式( 4) 就可以求出边缘点的准确位置。

      根据最小二乘原理( 残差平方和最小) , 有:】

     最小化误差后, 就可以求出系数k0, k1, ⋯, k5的值。以边缘点为中心, 建立极坐标系, 将x=ρcosθ, y=ρsinθ代入所得的曲面拟合函数里, 得到在梯度方向上关于极径的二次曲线方程, 对这个方程求取其极大值, 即可得到准确的边缘点的位置:

      在上面求解k值的过程中, 需要注意到的一点,就是二次曲线是由原高斯曲线取对数后得到的, 因此求解时应将象素点的灰度梯度值用其对数值代替。这样, 边缘点亚象素位置的提取公式为:

3 实验结果

      本课题实验采用的是型号为MTV- 2821CB的黑白CCD摄像机, 工作台是JX14A数字式工具显微镜。图2中a) 图是通过CCD摄像机拍摄到的精密小孔原图, 测量时, 通过前后左右移动工作台, 使小孔在成像视场中的位置发生变化, 采样10次, 运用本文所提出的方法测量小孔的直径, 得到的实验数据如表1所示。

     从表1的测量结果中可以看到, 测量结果的精度达到了0.868 μm, 取得了比较好的效果。

4 结论

     本文首先提出了高精度零件尺寸测量系统的结构、工作原理等问题。然后提出了一种在Sobel算子的基础上去掉局部非极大值点来快速获得象素级边缘的方法, 进而提出在梯度方向上进行高斯曲线拟合插值来提高测量系统的精度, 从实验结果中可以看出, 取得了比较好的效果。