微型移动龙门式铣床结构优化设计
2018-12-5 来源:重庆交通大学机电与车辆 . 四川永贵科技 作者:安治国 刘奇 卢飞
摘要: 针对某微型移动龙门式数控铣床的结构薄弱处,提出一种基于拓扑优化以及正交试验设计方法的整机优化设计方法。首先,建立其本体有限元模型,在具体工况下对其进行了静力学分析,得到了位移、应力云图; 通过模态分析,得到其前十阶模态固有频率和主振型。根据有限元分析结果,基于拓扑优化原理,以最小应变能为目标函数,立柱质量为约束条件,对微型铣床立柱进行了优化设计; 采用正交试验的方法,以工作台自重下最大位移为优化目标,T 形槽大小、槽间距、工作台厚度和工作台支撑面积为设计变量,对作台进行了优化设计。最后对优化后整机结构进行了有限元仿真,结果表明优化后整机静动态性能有了明显提高。
关键词: 微型铣床; 有限元; 模态分析; 优化设计
0 引言
微型移动龙门式铣床常用于小型零件的加工,为了提高其刚性及加工精度需对机床的本体结构进行优化设计。在机床结构优化方面,有很多学者做了相关研究。何剑等采用拓扑优化与有限元仿真相结合的方法对微细加工机床的立柱进行优化设计最终确定立柱的最佳结构模型。王滕等对机床床身进行模态分析,根据分析结果对床身横梁和立柱进行优化设计。宋宇等提出一种综合优化技术对机床床身结构进行优化设计。
但在机床结构优化的研究中,目前多数学者只关注于对结构单个部件进行优化设计,缺乏对多个关键部件综合考虑,更缺乏对整机静动态性能的优化和分析。改变机床的结构,提高结构的刚度,同样对机床的精度影响较大。
本文以某微型移动龙门式铣床为研究对象,对其本体结构进行有限元仿真,分析其静动态特性,辨识机床的薄弱环节,指出立柱与工作台对整机性能影响最大。以立柱与工作台为优化目标,对机床结构进行优化设计改善机床的静动态性能。
1 、机床模态分析理论
微型移动龙门式铣床可看作一个 N 自由度线性系统,其运动微分方程为:

2 、有限元模型的建立
2. 1 微型铣床本体结构
微型移动龙门式铣床整体外形尺寸为 900mm ×700mm × 655mm,工 作 行 程 为 500mm × 400mm ×150mm。其本体结构三维模型如图 1 所示。
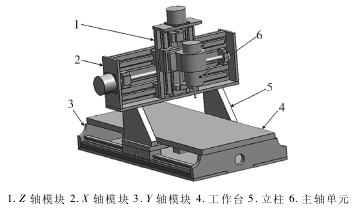
图 1 微型移动龙门式铣床三维模型
2. 2 有限元网格划分
综合考虑计算效率和精度,对该铣床几何模型进行适当简化,忽略进给电机及传动系统对本体结构的影响,主轴电机作为刚体,选择刀位点为刚体参考点; 去除螺纹孔和部分倒角等细小特征; 整机机架均为 45 钢,可作为一个整体建模; 导轨和滑块与机架接触部分粘接为一体,导轨与滑块间同样选择粘接。
选择六面体单元C3D8R 划分网格,总共得到 37663 个单元。
2. 3 材料参数
机床本体主要采用为 45 钢,其密度为 7800kg/m3,弹性模量为 2 × 105MPa,泊松比为 0. 3; 导轨材料为GCr15,密度为 7810kg / m3,弹性模量为 2. 08 × 105MPa,泊松比为 0. 3; 滑块材料为 20Cr Mo 合金钢,密度为 7850kg / m3,弹性模量为 2. 06 ×105MPa,泊松比为 0. 3。
2. 4 工况的确定
刀具 直 径 为 10mm,齿 数 为 4,切 削 速 度 为 25m / min,进给速度为 200mm / min,背吃刀量为 0. 3mm,切削宽度为 7. 5mm,每齿进给量为 0. 03mm。铣削力Fz
根据铣削力经验公式计算可得为 48N。
3 、结果与分析
3. 1 静力学分析
在刀具刀位点 X、Y、Z 三个方向分别施加 48N 的切削力。通过计算得到位移和应力云图如图 2 所示。

图 2 静力学分析位移、应力云图
通过图 2 可知,综合位移为 2. 73 × 10- 2mm,最大应力为 1. 89MPa 远小于 45 钢的屈服强度为 355MPa,表明该铣床满足设计要求。关键点刀位点与工作台中心位移量分别为 1. 024 × 10- 2mm,1. 62 × 10- 2mm。总体看来,立柱设计趋于保守,立柱需做进一步轻量化设计; 工作台的最大位移偏大,即工作台静刚度偏低,需要对工作台进行进一步优化,提高其静刚度。
3. 2 模态分析
机床导轨滑块结合部模型采用弹簧阻尼单元建立,其 他 结 合 部 模 型 均 与 静 力 学 模 型 一 致。采 用ABAQUS 中的 Lanczos 求解器进行模态分析,提取了前10
阶模态频率及其主振型,如表 1 所示。
表 1 微型铣床前十阶振型表
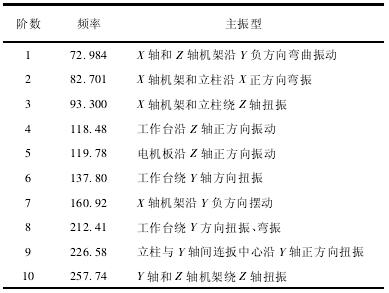
由于篇幅有限只列出前四阶振型图,如图 3 所示。

图 3 铣床前四阶振型图
由表 1 和图 3 可知,机床前十阶的固有频率相差较大,机床整体有一定的抗震能力。第 4、6、8 阶模态为工作台的振动变形,工作台的变形影响到工件的加工精确,需要对工作台进行优化设计。另外,由于立柱以上的床身扭振,引起刀具的摆动较大,对铣削精度影响较大,分析其原因为立柱与 X 轴连接部分尺寸较小,从而造成连接部位刚度不足。
因此需要增大工作台本身及立柱与 X 轴床身连接部位的刚度。
4 、机床的优化设计
4. 1 立柱结构优化
综合考虑,立柱优化选用通用拓扑优化算法对其进行优化设计。以设计区域伪密度为设计变量,结构应变能最小为目标函数,质量减小 35% ,最大位移不超过 2. 3 ×10(- 4次方)mm 为约束条件进行拓扑优化,设计区域如图 4 所示。
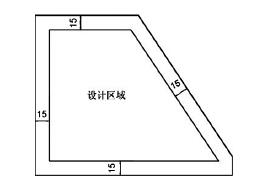
图 4 设计区域
将立柱下表面约束,在上表面施加 0. 2MPa 的面压力,并在质心施加重力加速度。通过有限元仿真,得到立柱拓扑优化结果如图 5 所示。
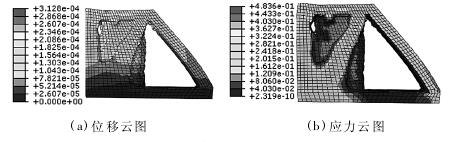
图 5 立柱拓扑优化结果
根据优化结果,将立柱的三维模型进行修改,修改后的模型如图 6 所示。
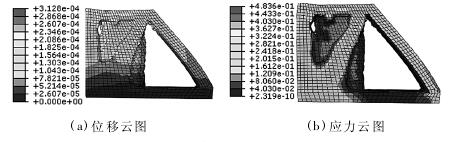
图 6 优化设计后立柱三维模型
4. 2 工作台优化设计
工作台的优化采用正交试验设计方法。为提高机床加工精度,将工作台静刚度作为优化目标,试验的指标为静力学条件下工作台的最大位移。选择 T 形槽大小、T 形槽间距、工作台厚度、工作台支撑端边长 L 四个因素分析,因此选择正交试验表 L16( 45) ,因素水平表如表 2 所示
表 2 因素水平表
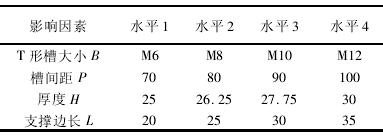
各因素对目标函数的影响如图 7 所示,得出最优组合水平值分别为 1、2、4、4,即 T 形槽大小为 M6,槽间距 为 80mm,工 作 台 厚 度 为 30mm,支 撑 边 长 为35mm,认为是最优组合。
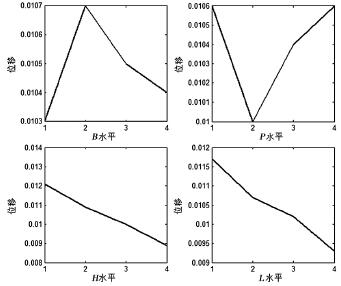
图 7 各因素位移估算边际均值
4. 3 优化后整机有限元分析
为了验证优化后整机静动态特性,首先对机床进行静力学分析,仿真结果如图 9 所示
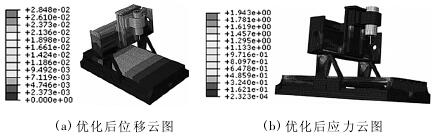
图 8 优化后静力学分析位移、应力云图
由图 8 可知,综合位移为 2. 85 × 10- 2mm,变化不大,最大应力为 1. 94MPa 远小于 45 钢的屈服强度为355MPa,满足设计要求。关键点刀位点与工作台中心位移量分别为 0. 95 × 10- 2mm,0. 82 × 10- 2mm。通过静力学分析可以看出,整机关键点位移比优化前明显减小,达到优化目的。
通过对比优化前后结构的模态可知,机床低阶频率有较大的改善,机床的整机动态性能得到有效提高,如图 9 所示。
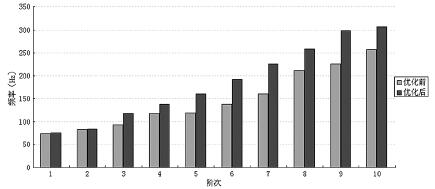
图 9 优化前后模态对比
5 、结论
通过有限元分析结果表明,机床在结构优化后整机静态性能与动态性能都有一定提高,验证了结构优化的有效性。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com




