摘要:机床刚度、固有频率等动力学特性随着机床部件位置、姿态在工作空间中的变化而变化。对机床动力学特性的研究不仅需要考虑到机床质量、刚度、阻尼值的大小,还应重视机床加工点的空间位置变化。采用空间统计学方法,以超精密机床固有频率这一关键动力学性能为例,分析机床动力学性能与机床位置姿态之间的数学关系,选取机床动态特性变异函数,建立动力学性能变化预测的Kriging 方法模型,研究动力学特性在工作空间中的变化规律以及动力学特性空间信息的表述方法。将所建立的模型与正交多项式方法、径向基神经网络方法、二阶响应面方法等方法建立动力学性能预测分析模型比较,空间统计学Kriging 方法所建立的模型R2 检验大于0.96,在四种模型建构方式中为精确度最优,能够在完整工作空间中准确地描述机床动力学特性。基于空间统计学的机床动力学特性研究为机床的动力学设计提供了新的设计分析方法及相应的技术支持。
关键词:机床动力学;加工空间;空间统计学;Kriging 模型;固有频率
0 前言
机床动力学特性是机床重要的性能指标。不恰当的机床设计和使用将引起机床加工中的颤振,使得机床的切削条件变得不稳定,导致刀具的磨损和断裂,产生加工中的振动和噪声,影响机床加工精度和工件表面形貌,加速机床本身的磨损和破坏。与机床动力学性能相关的机床设计参数通常有机床的刚度、固有频率、模态振型、阻尼、质量分布等。机床动力学特性设计和分析通常采用有限元方法建立虚拟仿真环境[1-3],提供在一个具体的位置和姿态下,机床的n 阶固有频率和对应的模态振型以及刚度,为机床的动力学设计提供数据支持。虚拟仿真环境解决了机床运动过程中的位置相关的动力学性能评估问题,但尚未对机床各加工位置之间的动力学性能的变化趋势和关联性进行分析。针对机床工作空间中动力学特性的演变,许多学者进行了分析研究。ZAGHBANI 等[4]采用机床加工过程中模态的变化为指标来评估机床动力学特性的稳定性。WU 等[5]分别使用数值计算和试验方法研究了5自由度混联机床工作空间中的刚度分布,并尝试通过改进刚度最低的部件刚度来优化系统刚度。刘海涛等[6]通过定义广义加工空间函数的方法,在龙门机床和立式机床的整个工作空间进行模态分析和动力响应分析,获得了低阶固有频率在加工空间中变化最大可达25%的结论,证明了机床性能的优化中完整模态信息的重要性。但目前,关于动力学特性在工作空间中的变化规律的研究以及动力学特性空间信息的表述方法的研究还未见有详细研究的报导。
本文通过机床工作空间动力学特性分析机床动力学性能的空间特性的内在形成机制,继而,以一阶固有频率为例,建立空间中的机床动力学特性的空间统计学模型,通过与正交多项式模型、神经网络模型及二次响应面模型的比较,分析动力学性能的影响因素的同时,获得高精度的空间动力学特性表征模型。
1 、机床动力学性能的空间特性分析
如图 1 所示[7],机床刚度、固有频率、模态振型等动力学参数是机床关键部件及结合部组成的刚度链[8-10]结构特性和机床空间位置、姿态等空间特性的函数。刚度链随着机床的位姿变化而变化。刚度链每一位置姿态对应的刚度、固有频率等模态信息都可以使用多体动力学和有限元分析的联合仿真方法求解[2]。

图1 机床刚度链及机床动力学特性
机床刚度链的两个端点刀具和工件在加工过程中位置变化包络形成机床工作空间。加工空间内的质量矩阵、阻尼矩阵、刚度矩阵随着机床位置姿态的变化而变化,并引起固有频率、模态、动刚度等动态特性的变化。其中,质量矩阵在加工过程中随着运动部件重心的变化而变化;阻尼产生机理和计算方法尚有争论;机床的刚度链组成复杂,包括:结构件刚度、主轴刚度、导轨刚度、结合部刚度、电机伺服刚度、气浮轴承刚度等,在机床运动过程中,这些刚度链的刚度变化量级不同。在三个因素综合作用下,机床的固有频率、模态、动刚度等动态特性在加工空间中的变化呈现非线性、变化规律复杂。
决定机床动力学特性的机床质量矩阵 m、刚度矩阵k 和阻尼矩阵c 都随着刚度链的变化而变化,机床的动力学特性是空间位置(x, y, z)的函数。可写为

将位置姿态数据(x, y, z)反复代入到式(1),获得某5轴铣床各加工位置的一阶固有频率,如图2 所示。对式(1)、(2)进行模态叠加,可得到由固有频率值和模态矢量表述的动刚度等动态特性

根据以上数学推导及分析可知,由于机床运动中质量、阻尼、刚度改变的连续性,加工空间中的动力学特性数据各位置间明显具有关联性,表现为邻近位置的动力学特性相似。这种数据之间的关联性,使得超精密机床加工空间动态性能具有空间依赖性(空间自相关)。在进行动态性能分析时,既考虑到各采样点具体值的大小,又重视样本空间位置及样本间的距离的方法会更有利于动态性能的把握。空间对象间的相关性和非独立的有效科学方法是基于数据的空间统计学。从这个性质而言,传统的代数多项式拟合建立在数据独立性的基础上,代数多项式的统计模型对空间数据的分析会产生虚假的解释。目前流行的神经网络方法没有在算法中明确指出从空间特性上对动态性能学习和分析的途径,其对整机动态特性的掌握也没有考虑空间数据关系的空间分析方法精准。在空间特性分析上,Kriging 方法[11-12]是以已知样本信息的动态构造为基础,充分考虑到变量在空间上的相关特征,建立对象问题的近似函数关系来模拟某一点的未知信息的有效空间统计学方法。

图2 加工空间各加工位置的固有频率值
因此,本文尝试使用 Kriging 方法建立近似模型对加工空间动态特性预测分析,并与传统代数多项式建立的响应面近似模型、及基于对数据学习分析的神经网络模型对比,以期获取更好性能预测分析。
2 、动力学性能的Kriging 预测模型
Kriging 插值[11]是一种求最优、线性、无偏的空间内插方法,采用协方差衡量各点空间相关程度。它是基于线性回归分析的一种改进,模型包含了线性回归部分和非参数部分,其中的非参数部分被称为变异函数,采用随机分布函数的实现。
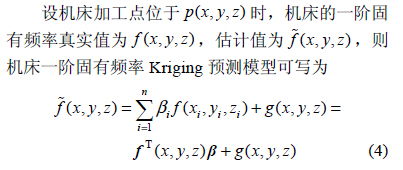

常用于拟合变异函数的模型包括指数模型、高斯模型、Matérn 线性模型、Matérn 立方模型。通过计算模型协方差,找出最佳理论变异函数模型,获得最好拟合效果,计算公式为




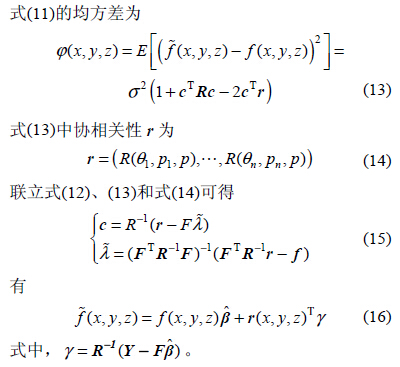
至此,对加工空间中任意点的一阶固有频率可使用式(16)计算获得。其他如刚度、高阶固有频率、阻尼等相关动态性能参数均可使用此方法计算。下面以一阶固有频率为例对Kriging 方法建立的模型进行加工空间内机床动态特性分析。
3 、机床动态特性分析
3.1 动态特性变异函数的选择
取图 2 中27 个空间点作为位置变量输入P = {p1, p2 ,, pn},对应响应变量的输出数据f1,f2.... fn,计算刀具加工点位于空间位置p 时机床的动态性能。
将已知的 27 个空间位置的一阶固有频率数据代入,选择变异函数g(x, y, z)协方差计算模型为指数模型,获得正则化θ 参数如表1 所示。
表 1 Kriging 模型θ 参数

至此,完成整体模型拟合。



图3 指数函数模型频率预测值与真实值比较由于 Kriging 模型建立时考虑了数据的内在相关性,所有变异函数获得的近似模型拟合精确度检验R2 检验值均大于0.95,四种变异函数都可以比较精确地表达一阶固有频率在加工空间内的变化规律。四种模型中指数函数模型能够更好地表达数据之间的相关性,近似精度最高。
3.2 一阶固有频率的变化规律
以图 2 中的超精密铣床为例,研究机床加工空间中一阶固有频率的变化规律。

图3 指数函数模型频率预测值与真实值比较
图 4 中X 剖面从左到右依次为x=-115 mm,x=0mm,x=115 mm。对三幅图中同一(y, z)点值分析可知,随着导轨在X 方向的移动,该超精密铣床工作空间中相同(y, z)位置一阶频率将产生6%非线性改变。图 5 中Y 剖面左到右依次为y=0 mm,y=112.5mm,y=225 mm。对三幅图中同一(x, z)点值分析可知,随着导轨在Y 方向的移动,工作空间的相同(x,z)位置一阶频率几乎没有发生改变。由此可知,能通过Y导轨运动到达的工作位置,应优先移动Y导轨。如图 6 所示,图中Z 导轨位置从左到右依次为z=0 mm,z=80 mm,z=160 mm。随着导轨在Z 方向的移动,工作空间中相同(x, y)位置一阶频率将产生5%的非线性的改变。由于Z 方向是加工敏感方向,这种变化在超精密加工中产生影响需要尽量避免。对三幅图中同一点值分析可知,当Z 导轨位于定导轨中部(z=80 mm)位置时,工作空间中(x, y)点位置的变化对整机频率影响最小。

图4 工作空间内的一阶频率(X 剖面)

图5 工作空间内的一阶频率(Y 剖面)

图6 工作空间内的一阶频率(Z 剖面)
根据以上分析可知,机床的一阶固有频率在工作空间是变化的,为了保持机床工作的平稳,应优先使用频率变化小的运动方式来保障机床具有更平稳的动态性能。以文中所使用的超精密铣床为例,该机床在工作时应该尽量使得Z 导轨停留在定导轨的中部,优先进给Y 轴,减少X 导轨的运动来降低超精密加工中机床性能变化对精度带来的不利影响。
4 、对比研究
机械设计分析中,传统上更多地使用包括正交多项式模型[14-15]和响应面模型[16-17]等多项式近似模型。近年来,神经网络模型[18-19]作为近似分析模型在机床建模和机械产品性能分析中也日益广泛使用。本节测试这三种模型在机床动态特性分析中的适用性。
4.1 正交多项式模型
将 上 述 27 个采样点作为输入点, 采用CHEBYSHEV 正交多项式建立机床一阶固有频率的空间动态模型。可解得R2=0.471 63,由于R2 小于0.9,误差值过大,这种算法构建的一阶固有频率空间变化规律模型用于分析时可信度非常低。
计算出的一阶固有频率预测值与真实值比较及一阶固有频率分布如图7、图8 所示。由于误差值过大,可认为这种构造近似模型的方法得到的近似模型用于分析时可信度较低。

图7 正交多项式近似模型频率预测值与真实值比较

图8 正交多项式近似模型仿真结果
4.2 径向基神经网络模型
径向基神经网络模型形参数取值 2.97,构造后得到R2=0.885 47。残差分析如图9 所示,仿真模型如图10 所示。由于误差值过大,可认为这种构造近似模型的方法得到的近似模型用于分析时可信度较低。

图9 神经网络模型模型频率预测值与真实值比较
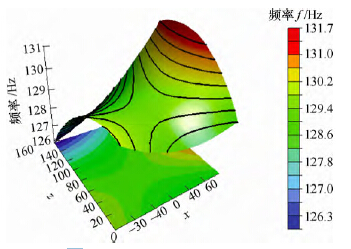
图10 神经网络模型仿真结果及分析
4.3 二阶响应面模型
根据给定的 27 个点的初值,可写出二阶响应面模型(Response surface method, RSM)构造方程。二阶响应面模型R2=0.346 71,精确度分析如图11 所示,频率分布仿真效果如图12 所示。由于R2 远小于0.9,误差值过大,可认为这种构造近似模型的方法得到的近似模型用于分析时可信度非常低。

图11 RSM 近似模型频率预测值与真实值比较
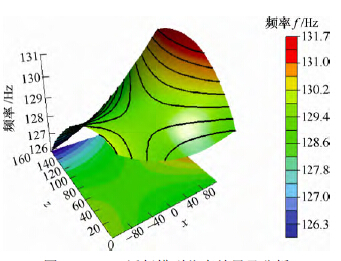
图12 RSM 近似模型仿真结果及分析
5 结论
(1) 本文使用Kriging 方法建立空间统计模型进行机床动力学特性研究,获得了固有频率、刚度在加工空间分布规律,在完整工作空间中准确的描述超精密机床动力学特性。
(2) 机床动力学特性的刚度、固有频率等主要因素随着机床位置姿态的变化规律可使用Kriging方法描述。方法中的四种变异函数模型(指数函数、高斯函数、线性函数、三次函数),指数函数模型能够更好的表达数据之间的相关性,近似精度最高。
(3) 由于正交多项式模型、响应面模型和神经网络模型在模型建构中使用了数据独立性假设,该假设与机床动态特性数据的空间相关性相违背,所以不适合用于机床动力学特性变化规律的描述。本文的研究结果为超精密机床的动力学设计提供了新的设计分析方法和技术支持。为机床使用中加工位置和姿态的选择和路径规划提供了原理和数据支持。
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com




