基于灵敏度的换刀时间和工艺动态可靠性研究
2019-8-19 来源:东北大学机械动力学 哈尔滨工业大学 作者:王新刚 陈晓明 闫明明
摘要: 将刀具的切削参数作为随机变量,结合矩估计、最大似然估计和动态可靠性分析技术,建立了机加工艺系统的动态可靠性数学模型,推导了各工序刀具的失效率计算公式; 以刀具失效率为判据,建立了确定临界刀具及换刀时间的方法; 在此基础之上,以最大限度利用刀具为研究目标,在确定被更换刀具的同时应用可靠性灵敏度分析方法确定刀具最敏感切削参数,通过改变最敏感的切削量参数提升刀具及整体工艺系统的可靠度,使刀具能够继续工作,延迟换刀时间; 研究结果表明: 当整体工艺流程系统可靠度低于某一阚值时,应用该模型能够迅速准确找出失效率最大的工序所使用的刀具并对其敏感参数进行控制,从而确保刀具还能满足工艺可靠性要求,最大限度的利用刀具,减少换刀次数,降低成本,保障整体工艺系统的高可靠性。
关键词: 工艺; 刀具; 可靠性; 灵敏度; 换刀时间
现代社会,机加工行业对产品加工工艺过程中的安全性和可靠性提出了更高的要求。机床、人和刀具之间的稳定性具有相关性,每一个环节都是一个不可忽视的系统,所以研究刀具的可靠性具有重要的工程意义。
如果刀具可靠性差,就会出现崩刃现象,导致产品加工精度不合格而产生废品,浪费工时和加工成本。Ramalingam 和 Watson[1]等进行了刀具可靠性研究,建立了刀具耐用度概率模型。Wang K S 等建立了考虑衰减因素在内的刀具磨损可靠性数学模型。哥伦比亚的 Carmen[3]研究了加工过程中刀具磨损与可靠性的关系,并且将可靠性概念用于切削换刀时间处理。
国学者 M. Kronenberg[4]首先针对端铣加工切入类型与刀具破损之间的关系进行了研究,解决了切入类型对可靠性影响的计算问题; 美国学者Mazzuchi 和 Soyer[5]建立了基于泰勒公式的数控机床刀具可靠性模型,用于计算加工过程参数。目前国内外学者都没有考虑将刀具的可靠性作为影响换刀时间和机加工艺的重要因素。
除此之外,由于切削振动、被加工产品的内部结构均匀性等因素的影响,切削参数一般是随机变化的,作为随机变量更贴近真实工况,但关于切削参数对刀具可靠性影响程度即可靠性灵敏度及换刀时间和整体工艺流程可靠性的影响还未见到有关报道。
文将可靠性灵敏度知识融入到机加工艺流程中,建立基于灵敏度的临界刀具和换刀时间的机加工系统动态可靠性数学模型。通过灵敏度技术在刀具失效之前或者换刀之前找到敏感的切削参数并对其进行控制,以达到提高刀具可靠性及整体工艺流程可靠性的目的,最终实现刀具的最大限度应用,节约成本。
1 、建立工艺流程的动态可靠性模型
每一道工艺的可靠性都与整体工艺可靠性密切相关,整体工艺可靠性受刀具、操作者和机器的可靠性影响。操作工人的可靠性可由实验获得,实验采用寄存器记录在给定观察期内发生错误的次数。机床的可靠度由自身结构设计所决定,包括工作环境、智能程度和管理与维修方案等等。
通常某台具体机床的可靠度数据由“无故障时间数 据 库”获得[6]。本文主要研究刀具的可靠度,在研究过程中没有考虑操作工人和机床自身的可靠度。在加工产品时,机床、刀具、机床和操作工构成了一个串联系统,每个子系统相互独立,那么整个产品机加工艺流程的可靠度为
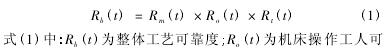

为表述方便,在实际加工中以加工零件个数 N 为计时单位。若加工某零部件需要一个完整的工序共包含 n 道,且在进行第 i 道工序时刀具的切削时间为 ti,该道工序刀具的可靠度为 Rti,加工该零部件的整个工艺可靠度可以看作由 n 个串联的子系统组成的可靠度。
由式( 2) 和式( 3) 可知,当加工了 N 个部件时,其第 i 道工序刀具的可靠度为
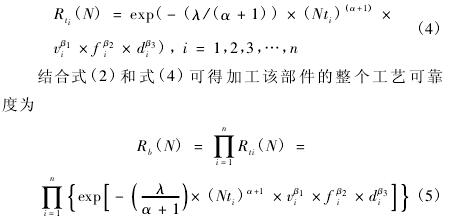
由式( 5) 可知,当 n = 1 时,其表示为整体工艺只含有一道工序时的可靠度。
2 、刀具的可靠性灵敏度分析
假设各切削参数相互独立,运用已有的相关理论[8 - 9]易知各基本随机变量的均值与方差均可通过矩估计法求得,根据微分法可分别计算得出可靠度关于切削速度 v、进给量 f、切削深度 d 等基本随机变量的可靠性灵敏度[10]。由式( 3) 得各工序刀具的可靠度 Rt( t) 对切削速度 v 的灵敏度为4 同理可得,各工序刀具可靠度对进给量 f,切削深度 d 的灵敏度分别为
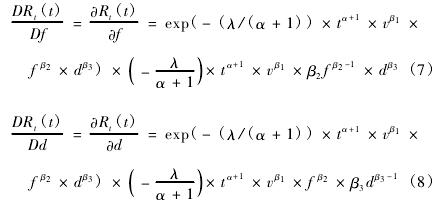
若以加工零件的个数 N 为计时单位,设第 i 道工序的工作时间为 ti,则最终可得灵敏度随加工零件个数的变化规律为
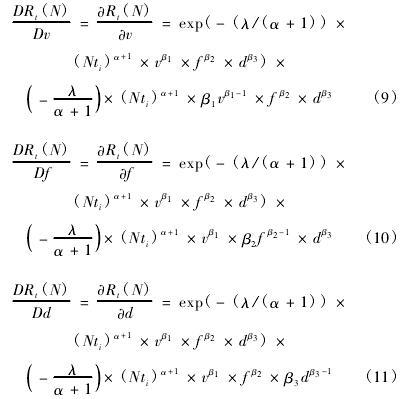
若某参数的可靠性灵敏度数值为正,表示该参数随着均值的增加,刀具的可靠度将增加; 相反,若该参数灵敏度数值为负,则随着该参数均值的递增,刀具将更易失效。若可靠性灵敏度的绝对值较大,则表明刀具对该参数的变化较为敏感,应加以控制,以保证产品和整体工艺的可靠性要求。
3 、工艺流程换刀时间
3. 1 工艺流程只有一道工序时的换刀时间
根据式( 5) 易求整个工艺流程的可靠度,当加工至某个数量的零件发现计算出的可靠度数值低于产品的许用值时( 这里设为 0. 8,根据实际加工要求该许用值可以任意调整) ,就应该更换刀具,否则会产生废品,增加经济成本,那么在何时更换刀具,如何更换刀具显得颇为关键。下面将对换刀时间进行详细分析。当整个工艺流程只有一道工序时,以加工零件的个数 N为计时单位,根据式( 4) 可计算出可靠度,变化曲线如图 1所示。
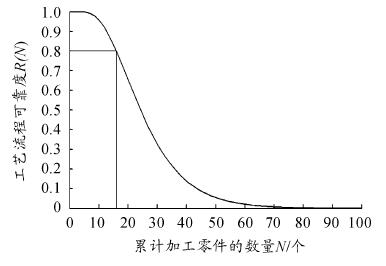
图 1 工艺流程可靠度的变化曲线( 只有一道工序)
当工艺流程可靠度的值低于许用值 0. 8 时,必须进行换刀,且直至达到目标产量之前可能需要进行多次换刀。设工序的工作时间为 t,则换刀时间 Tc为 7 每次换刀前后可靠度曲线如图 2 所示。
在图 2 中,N1、N2、N3、N4是换刀时间节点和换刀时已经加工完的零件数。这里对整体工艺流程可靠度设定一阚值0. 8,要求在任意时刻整体工艺流程可靠度必须大于这个阚值。当在 N1点换刀时,从图 2 可以看出整体工艺可靠度由原来 0. 8 提升致 0. 97 的位置; 当在 N2点换刀时,加工该部件的整体工艺可靠度由 0. 82 升至 0. 95。
为何第 2 次换刀选择整体工艺可靠度高于阚值而不是低于阚值,是因为如果不更换刀具再继续加工一个部件后有可能使整体工艺可靠度低于阚值 0. 8,会导致出现废品或者停车事故。从图 2 可以看出,只要及时准确的确定要替换的刀具和换刀时间,就能够保持整体工艺流程可靠度高于阚值。
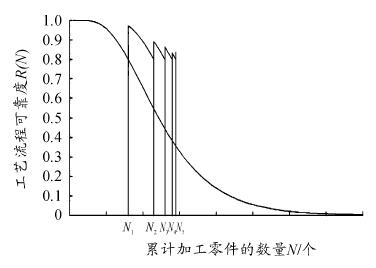
图 2 每次换刀前后可靠度的曲线
3. 2 工艺流程含有多道工序时的换刀时间
在加工某一零部件时会包含多道工序,假设每一道工序使用的刀具是不一样的。首先应根据式( 5) 计算出整个工艺流程的可靠度并与许用的可靠度进行比较,若低于许用值,则必须进行换刀。由于刀具的不同,选择更换的刀具是主要问题。采取逐个计算刀具失效率的方法确定需要更换的刀具。临界刀具为失效率最大的为临界刀具。已知刀具的失效概率函数为
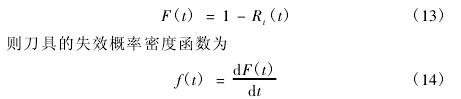
将式( 13) 代入式( 14) 得
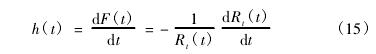
由前述可知,假设一个完整的工艺流程共含有 n 道工序,且第 i 道工序的工作时间为 ti,则结合式( 4) 与式( 15) ,可得刀具的失效率函数为
10
3. 3 计算模型
从材料为 Q235 的钢板中切下长宽厚为 90 mm ×90 mm ×34 mm 的一段,需要经过钻削,铣削,铰等工艺过程。被加工件形状见图 ,具体加工要求见表 1 所示。
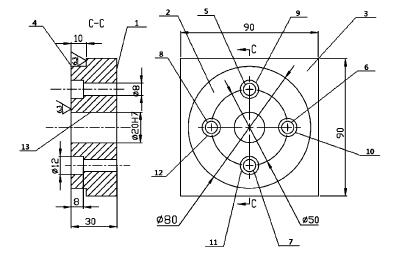
图 3 零件各部分结构及编号
表 1 盘类零件各部分加工要求
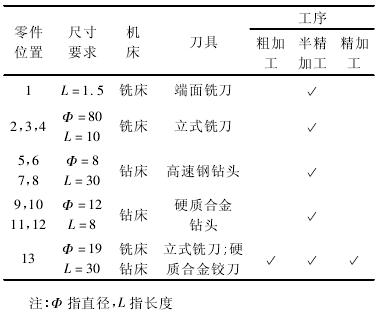
如图 3 可知,该部件划分为13 个部分,不同部分根据表面的不同特征采取不同的工序,然后确定工序顺序。由于加工条件及刀具自身材料的影响,刀具各切削参数均为随机变量,服从正太分布,操作工人假设不出现失误。通过 Master-cam 仿真可以得到各工序及其加工时间,具体结果如表 2所示。
由表 2 中的各参数构造其最大似然函数,可以求得 λ、α、β1、β2、β3,结果见表 3。
表 2 盘类零件各工序
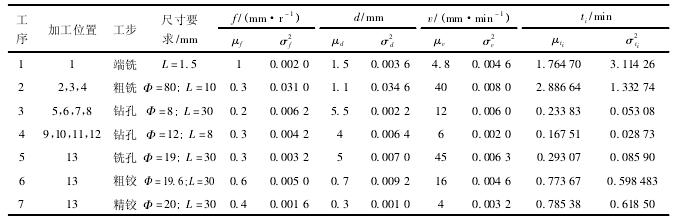
表 3 各工序的参数值
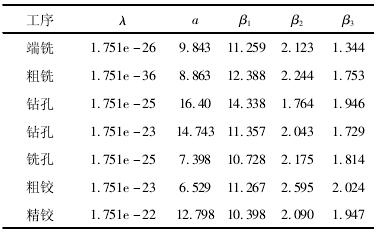
由式( 4) 可以计算出每道工序的可靠度,切削参数和每道工序工时见表 3,由式( 6) 可以计算出加工该部件时整体工艺可靠度。在此假设阈值为 0. 8,若整体工艺流程可靠度小于 0. 8 时,必须进行换刀。
此时通过式( 16) 可以计算出各刀具的失效率,并根据失效率大小确定更换刀具的工序与时间( 图 4) 。
在图 5 中,当加工第 18 个零件时,可计算整个工艺流程的可靠度为0.768 4,小于阚值0.8,说明在加工第17 个零件时应该换刀,此时是整个工艺的第一次换刀。
但具体更换哪个工序的刀具还需要再结合图 3。在加工第 18 个部件时,工序 5 对应的刀具失效率最高,需要更换掉。然后再重新计算整体工艺流程的可靠度,其值为
0. 998 4,使得整个工艺流程的可靠度得到提高。
各工序刀具可继续切削加工,直到整体工艺流程可靠度再次小于阚值 0. 8 时,进行第二次、第三次……换刀,直到完成所有需要加工的领部件。
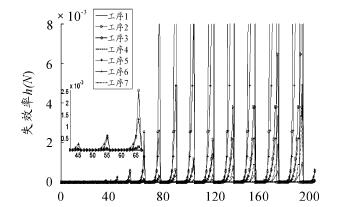
图 4 各工序刀具失效率对比曲线
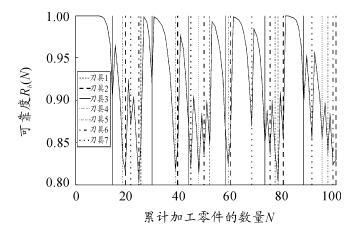
图 5 整体工艺流程可靠度曲线
4 、切削参数对换刀时间及工艺可靠性的影响
由式( 9) - 式( 11) 可得各工序刀具对 3 个切削参数灵敏度的变化曲线如图 6 ~ 图 12 所示。
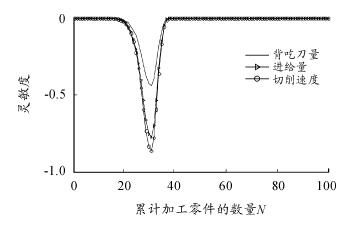
图 6 1 号刀具对切削参数的可靠性灵敏度变化曲线
从图 6 可以看出,第 1 道工序中刀具对切削速度 v 参数的灵敏度数值最大,即最敏感。从图 7 ~ 图 11 可以看出,第 2 道至第 6 道工序中刀具对进给量 f 参数的灵敏度数值最大,即最敏感。
从图 12 可以看出,第 7 道工序中刀具对背吃刀量 d 参数的灵敏度数值最大,即最敏感。由于刀具对切削参数的可靠性灵敏度均为负值,那么增加这 3 个参数的均值,会使刀具趋于不可靠,即工序失效。
所以在刀具失效之前就应适当降低最敏感切削参数的切削量,以达到降低均值提高刀具可靠性的目的,最终实现刀具的最大限度应用,节约成本。
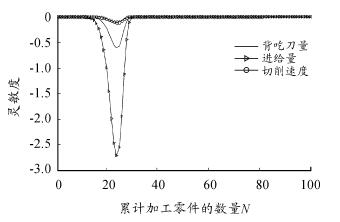
图 7 2 号刀具对切削参数的可靠性灵敏度曲线
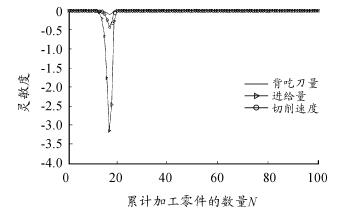
图 8 3 号刀具对切削参数的可靠性灵敏度曲线
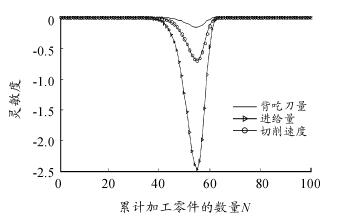
图 9 4 号刀具对切削参数的可靠性灵敏度曲线
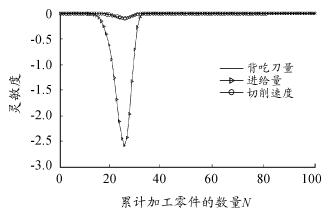
图 10 5 号刀具对切削参数的可靠性灵敏度曲线
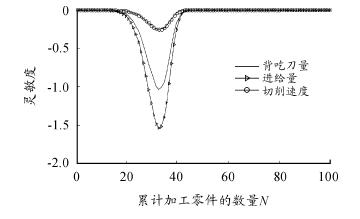
图 11 6 号刀具对切削参数的可靠性灵敏度曲线
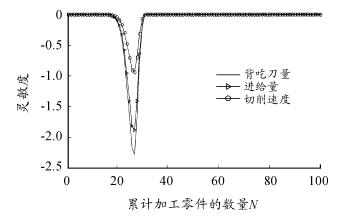
图 12 7 号刀具对切削参数的可靠性灵敏度曲线
在此规定当加工一定数量工件后已经根据前面的方法确定出换刀对象时,依据该刀具对切削参数的灵敏度图像确定出最敏感参数,然后对该参数的均值减半,增加工时,以达到提高该刀具可靠度的目的。当该刀具继续加工一定数量工件需要再次换刀时,将不再降低切削参数,直接更换新的刀具。以图 3 零件加工为例,结合可靠性灵敏度信息,得到关于延迟换刀的工艺流程可靠度曲线如图 13 所示。
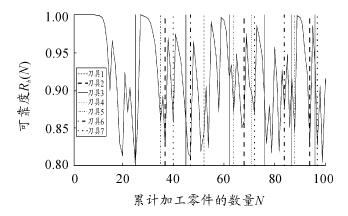
图 13 延迟换刀后整体工艺流程可靠度曲线
对比图 13 与图 5 可以看出,原来在图 4 和图 5 中可以判断出加工第 17 个零件就需要进行换刀,且更换的刀具为工序 5 中对应的铣刀。通过对该刀具进行灵敏度分析可得该刀具对进给量 f 参数最敏感,当加工第18 个零部件时不需要换刀,而是将该刀具进给量 f 变为 f/2 后继续加工,虽然工时有所增加,但是换刀位置却变到了加工第 26
个零件位置。
刀具 3 换刀时间由原来的加工工件数 20 变为 37,其他工序刀具均有所延迟。由此可见,加工完所有工件后,各工序刀具换刀时间均较以前有所延迟,在保证整体工艺流程可靠度的前提下减少了换刀次数,降低了成本。
5 、结论
本文提出的基于灵敏度的换刀策略方法能够提高刀具的使用效率和整体工艺流程的可靠度,从而实现了延迟换刀、降低成本的目的,可用于计算其他车、铣、刨、磨等工艺组成的完整工艺流程的可靠度,可用于系统的全生命周期管理,对正确评估刀具寿命和制定合理的换刀规划具有一定的指导意义。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息




