微铣削中考虑刀具跳动的瞬时切厚解析计算方法
2017-2-20 来源:上海交通大学机器人研究所 作者:聂强 黄凯 毕庆贞 朱利民
摘要:通过研究刀具实际切削过程中的余摆线轨迹及其影响,提出一种新的瞬时切厚解析计算方法,并针对两齿、四齿的情况给出瞬时切厚的具体计算公式。在两齿和四齿铣槽工况下,分析刀具跳动量和跳动角度对各齿切削过程的影响。该方法考虑刀具的综合径向跳动(包括主轴跳动,刀具制造安装误差等综合形成的径向跳动值),适用于微铣削中任意齿数刀具瞬时切厚的计算。通过与宏观铣削中的传统切厚计算公式、BAO 模型和Newton-Raphson 等数值法对比,量化指出了微细铣削加工与传统宏观铣削加工的一些不同,同时验证了提出的方法具有计算简洁、精度高和通用性强的优势。基于该模型进行了微铣削铣槽试验中切削力的预测,预测结果和试验结果相符良好,验证了模型的正确性和实用意义。
关键词:微铣削;加工机理;刀具跳动;刀具轨迹;瞬时切厚
0.前言
随着产品小型化需求的不断增长,微细加工机床被广泛用于医药、生物、航空航天、电子、通信等领域微小零件的加工。相比于传统机床或超精密机床,微细机床具有体积小、能耗低等优点。同时,微细切削加工技术成本低、效率高,可加工复杂的三维形貌特征,精度高,适用于各种材料的工件[1]。然而,微细铣削加工并不只是传统加工在尺寸上的微缩,它具有很多不同于传统切削加工的特征[2]。
首先是尺度效应[3]。在宏观切削加工中,刀具被认为是绝对锋利的。然而在微细加工领域,切削进给量与刀具切削刃的圆角半径相当,因而不再能忽略刀具切削刃的钝圆现象,并由此产生犁切现象和最小切屑厚度现象[1-4]。其次刀具跳动对切削过程影响显著。刀具跳动是制约微细切削加工质量的主要因素[5]。在微细切削中,由于刀具跳动量与每齿进给量相当,给切削过程带来严重的不稳定性,甚至导致某个齿空切。尤其对于二齿刀具,容易形成单齿切削现象。
因此能否在考虑刀具跳动的情况下,准确计算瞬时切厚,直接关系着切削力建模的准确性和可靠性,进而影响微细切削加工的质量控制。目前,微铣削中计算瞬时切厚的方法大致可以分为三类:不考虑刀具跳动的方法,考虑刀具跳动的数值法和考虑刀具跳动的解析法。不考虑刀具跳动的方法已经比较成熟,各类模型也比较多[6-8]。MARTELLOTTI[9]在20 世纪40 年代通过研究宏观铣削中刀具的轨迹及切厚,建立了宏观铣削切厚计算模型。2000 年BAO 等[6]从刀具的实际运动轨迹出发,给出了基于余偏摆线轨迹的切厚计算公式和切入角计算公式。2001 年LI 等[8]通过近似求解超越方程,得到不考虑刀具跳动的瞬时切厚计算公式,但由于公式本身的复杂性,难以在实际建模中使用。2013 年,KANG 等[10]建立用傅里叶多项式逼近的瞬时切厚计算公式,并与BAO和LI 的公式进行了计算结果的比较,比较结果表明其公式在计算上与LI 公式较为一致。
LI 等[11-12]采用Newton-Raphson 数值解法计算跳动下的瞬时切厚,但数值解法不利于建立解析形式的切削力模型。在考虑刀具跳动的解析法[7,13-14]中,BAO 等[7]给出了二齿情况下考虑刀具跳动的瞬时切厚计算公式。然而他们虽对四齿情况有作刀具跳动角度与切削力关系的分析,但没有给出四齿刀具考虑跳动下的具体的切厚计算公式。WAN 等[14]根据3 个不同刀具跳动模型的比较结果,推荐在切削力建模中使用径向跳动模型,并给出其切厚为宏观非跳动状态下的切厚值加上由跳动导致的相邻两齿实际半径差量值。该方法本质上依旧采用宏观上近似圆弧切削轨迹的简化思想。
本文目的在于通过分析铣削过程中刀具的实际切削轨迹,给出一个考虑刀具跳动的,能够适应于不同齿数的、解析的瞬时切厚计算公式。文章首先在考虑刀具径向综合跳动的情况下,建立了通用的切厚计算方法。随后针对刀具齿数N=2 和N=4等常见的情况,给出了具体的切厚计算公式,然后进一步分析了刀具跳动角度对各刀齿加工过程的影响,同时将新方法分别在对应齿数条件下与现有各方法进行对比,总结出新方法的优势。最后基于新切厚计算方法进行微铣削过程中切削力的预测试验,验证了新方法的实用性。
1.考虑刀具综合跳动的瞬时切厚建模
1.1 微铣削中刀具的实际轨迹
刀尖点的实际运动轨迹如图1 所示,呈余摆线状,灰色部分代表两条相邻轨迹所形成的切削厚度。
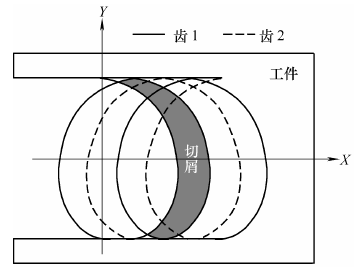
图1 两齿刀具切削时刀齿的真实轨迹
刀具切削刃的刃尖点,不考虑刀具跳动的情况下,其在笛卡儿坐标系XOY 中的位置可用如下方程表示[8]

考虑跳动情况下,刀具第i 个齿刀尖点在XOY坐标系中的方程为

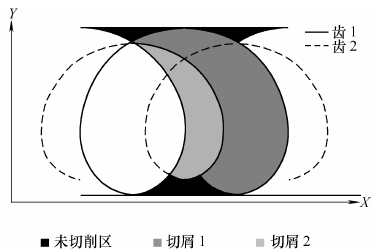
图2 考虑跳动下的两刃刀具各齿的切削轨迹及相应切厚示意图
从图2 可以看到,刀具径向跳动导致切屑1、2的厚度不同,刀齿1、2 每次参与切削的时间也不同。槽壁的实际加工轮廓(图2 中的黑色部分)要比没有跳动情况下的加工轮廓粗糙。刀具跳动易造成实际微细铣削过程的不稳定,降低加工质量。
1.2 考虑刀具跳动的瞬时切厚通用模型
下面将根据刀具的实际切削轨迹,利用参量间的几何关系,建立考虑刀具跳动的新切厚计算模型。

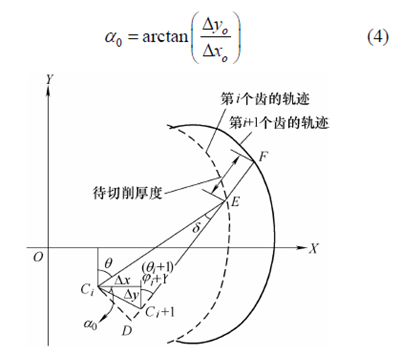
图3 槽铣中考虑跳动下的刀刃轨迹及瞬时切厚
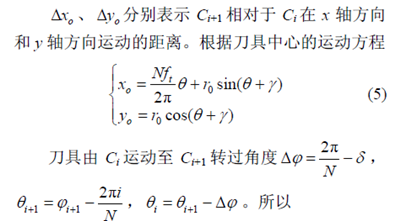
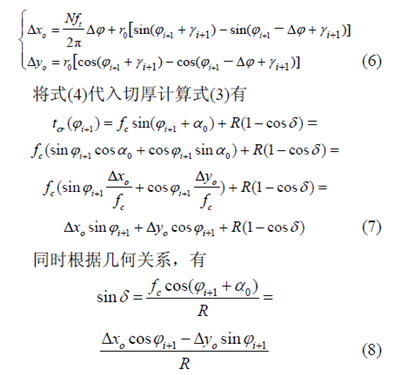

当发生空切时,有的切屑厚度并非由相邻两个齿的轨迹形成,如图4 所示。刀齿2 发生空切,刀齿1 的切厚应由刀齿3 轨迹和刀齿1 轨迹形成。而模型中刀齿1 的切厚根据齿2 轨迹计算,需要进行修正。由于齿2 切厚根据上述模型的计算值为负值,所以齿1 的切厚修正只需要将齿1 的切厚计算值加上齿2 的切厚计算值,即
若修正后,齿1 的最大切厚值也为负,则说明齿1 也发生空切现象,需要对齿1 的下一齿的切厚进行同样的修正。因此若i 齿发生空切,则需要对i +1齿进行切厚修正,修正方法和空切判定法如前所述。
上述模型适用于任意齿数下的瞬时切厚计算,本文在第2、3 节将讨论微铣削中最为常见的刀刃齿数为N=2 和N=4 的情况。
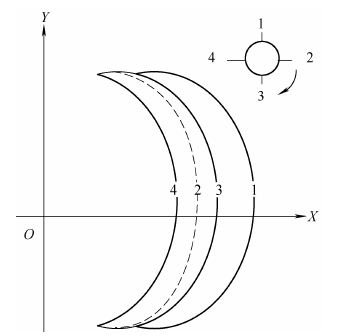
图4 空切现象示意图(刀具编号沿顺时针方向)
1.3 新方法与传统方法的比较
传统铣削过程中,由于 ft / R 的值通常非常微小,可将刀齿的切削轨迹近似为圆周曲线。本文将这种源于传统宏观铣削,基于近似圆周切削轨迹的切厚计算方法暂称为传统计算方法[8],其切厚计算公式采用

不考虑刀具跳动的情况下,记ε 为新方法计算结果与传统方法的计算结果的差值,用以衡量传统方法的计算误差。N=2 时,传统方法切厚计算结果相对于新方法的相对误差如图5 所示。图5 表明,随着 ft / R 逐渐增大,传统方法计算的待切削厚度误差将变得越来越大,而且在刀具的切入和切出位置达到最大。假设刀具半径为 1 mm,ft / R 的值为 0.1时,传统法计算误差最大达到6 μm 左右,这对微铣削过程中切削力的计算是影响非常大的。当 ft / R的值小于0.01 时,即传统的宏观加工工况下,新方法与传统简化法的计算结果则几乎一致。
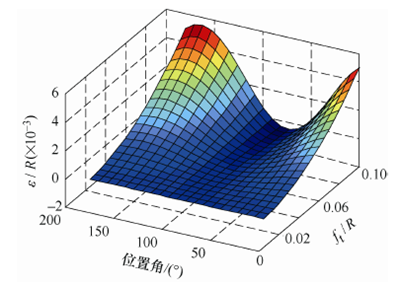
图5 N=2 的情况下,传统切厚公式的计算误差随 ft / R和θ 的变化规律


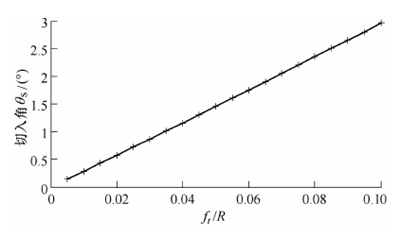
图6 r0=0 时,切入角随ft/R 的变化
随切入切出角的变化,槽壁侧表面加工轮廓的最大凸出高度可以通过式(15)进行计算
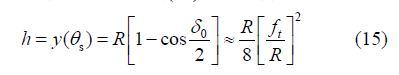
微铣槽后槽壁的表面轮廓高度正比于 ft / R 的平方。在刀具半径为 1 mm的条件下,当 ft / R的值为0.1 时,表面轮廓高度约为1.2 μm,仅相当于一般条件下半精加工的粗糙度水平。因此可知新方法比传统方法能够更好地描述实际微铣加工状况。
2.新方法下2 刃铣刀的切厚模型
2.1 N=2 时,具体切厚公式的导出及应用
当N=2 时,代入切厚计算公式(10),同时将
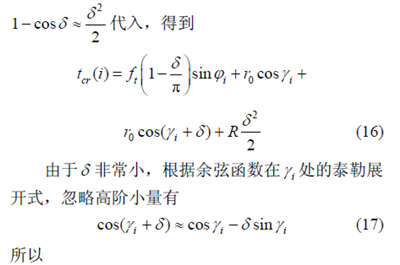
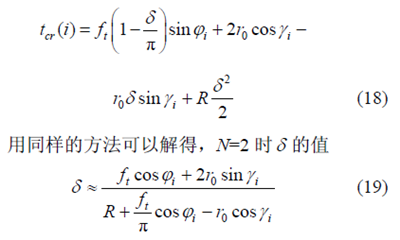
将式(19)代入式(18)便可以求得两刃刀具切削过程中考虑跳动的瞬时切厚。
根据式(18)、(19),在不同的跳动角度下,两刃铣刀在铣槽过程中的瞬时切厚变化规律如图7 所示,其中,N=2,R=500 μm, r0=0.2 μm, ft=1 μm/z。
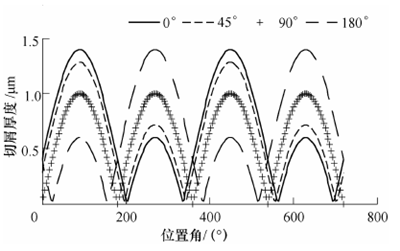
图7 铣槽过程中不同的跳动角度下的瞬时切厚变化:
考虑刀具跳动时,从图7 中可以看到,由于刀具跳动的存在,切厚以2π 为周期规律变化。当跳动角度为0°或者180°时,即刀具跳动方向平行于两齿的连线时,对切厚的变化影响最大,最大切厚将减小2r0。当跳动角度为 90°时,对切厚无影响。根据式(18),若2r0 cosγ i > ft ,便会发生单齿切削的现象。
2.2 N=2 时,新方法与BAO 方法的比较
若不考虑刀具跳动,即r0 = 0,代入式(18)、(19)可得
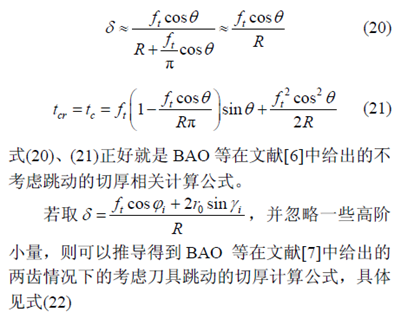
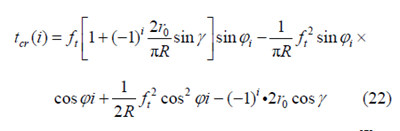
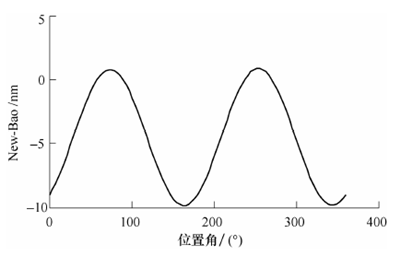
图8 新方法与BAO 方法计算瞬时切厚的相对误差
上述讨论不仅说明了新模型的正确性,而且可以看到,新方法统一了考虑跳动和不考虑跳动的两种情况下的切厚计算公式,也囊括了BAO 给出的考虑跳动情况下的切厚计算公式。并且式(18)、(19)在形式上的简洁为编程计算提供了更佳的选择。
3.新方法下4 刃铣刀的切厚模型
3.1 N=4 时,具体切厚计算公式的导出
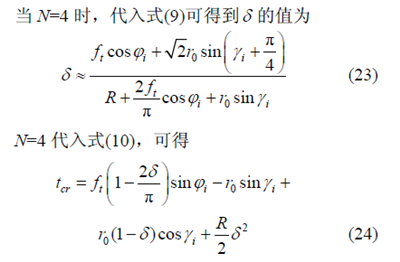

利用新模型,可以看到在不同的刀具跳动角度下,铣槽过程中四刃铣刀各齿的切厚变化如图9 所示,其中,N=4,R=500 μm,r0=1 μm,ft =3 μm/z。
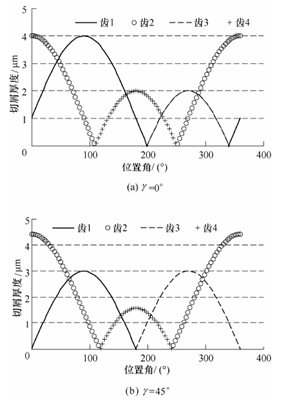
图9 在不同跳动角度下,各齿的瞬时切厚
从以上各跳动角度下四刃铣刀各齿的切厚变化可以看到,在槽铣过程中较厚和较薄的两个切屑总是相邻的,如图10 所示(在跳动角为0°的情况下,绘制各刀刃的实际轨迹及相应形成的切屑)。在跳动角度为45°的情况下,齿1、3 的切厚不受影响。所以为尽量减小跳动带来的影响,将跳动方向调整至45°是一个较佳选择。
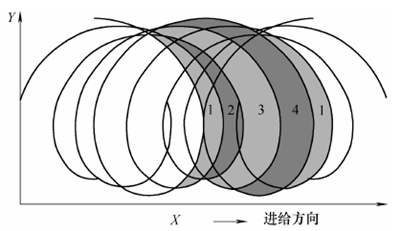
图10 考虑跳动下四刃铣刀各齿的切厚示意图
3.2 N=4 时,新方法、传统修正法与数值法的比较在考虑跳动的情况下,WAN 等在文献[14]中提到,径向跳动模型中,刀具的实际切厚应由式(27)进行计算
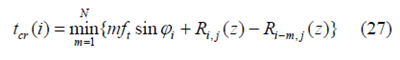
式(27)是在传统模型(式(12))的基础上作了考虑刀具跳动的修正,因此将其称作传统修正法。为了体现不同方法间计算结果的区别,以Newton-Raphson数值法的计算结果为标准,将新方法与传统修正方法分别减去数值法的计算值,所得结果作为解析法计算的相对误差,在N=4 跳动角度为0°的情况下进行对比。如图11 所示,其中,R=500 μm,r0=0.8μm,ft =2 μm/z。N-R 表示以New-Raphson 法为基准,新方法的计算精度明显比传统修正法要高,除个别位置角处,新方法与Newton-Raphson 法计算结果上几乎完全一致,相对误差率几乎保持为零。传统修正法由于没有细致考虑切入切出点的情况,在切厚接近于零的切入切出点附近,其相对误差率最大达到45%。而且随着刀具跳动量的增大,这一误差还会增大。新方法相比于数值法,则更简单高效,有利于建立封闭的切削力模型。
最后将新方法与其他切厚计算方法比较总结如表1 所示。在非数值法中,新方法是现有考虑刀具跳动下精度最高的方法。
表1 新方法与现有各切厚计算方法的对比总结
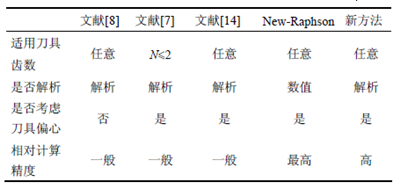
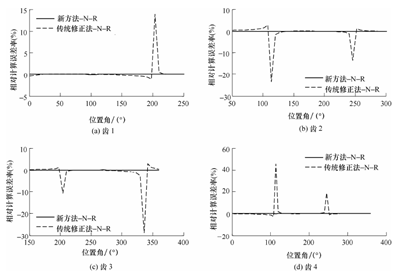
图11 新方法,传统修正法相对于数值法的计算误差对比
4.新切厚模型的试验验证
铣削力的建模采用微元法,即沿着刀具轴向,将刀具分割成一层层的小片,每一片上某一特定齿的切削厚度和位置角看成是一致的。如图12 所示,

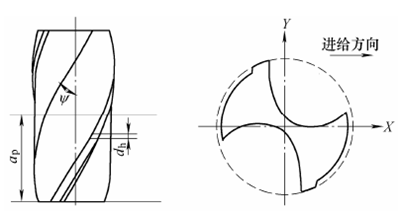



在文献[13]中,切厚模型采用传统不带跳动的计算方法,本文将基于新切削厚度模型,进行切削力的预测。
本文用直径为1 mm 的四刃硬质合金铣刀(中国台湾SGO-S550),螺旋角为30°,进行微铣削槽铣试验。工件材料为恒弹性合金3J53,其维氏硬度HV 为350~420,弹性模量为191~196 GPa。

图13 刀具和切削刃端面显微照片(左)及工件(右)
测力系统采用Kistler9317B 三向压电式测力仪以及配套的电荷放大器和数据采集系统。Kistler9317B 测力仪的灵敏度为0.01 N,X 和Y 方向量程600 N,Z 向量程2 000 N。采样频率为15 kHz。

图14 微铣削槽铣加工试验
试验切削条件为:刀具齿数N=4,刀具半径R=500 μm,主轴转速12 000 r/min,进给速度f=192mm/min,轴向切深ap=200 μm,X 方向为进给方向。刀具的跳动量在不同的转速下测量[7],其值在1~2μm 内变化,因此取平均刀具跳动量r0=1.5 μm,刀具跳动角度γ=35°。分别使用传统切厚模型和新的考虑跳动的切厚模型进行切削力的理论预测,效果如图15、16 所示。
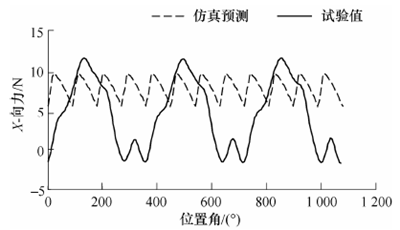
图15 基于传统切厚计算方法的切削力预测结果
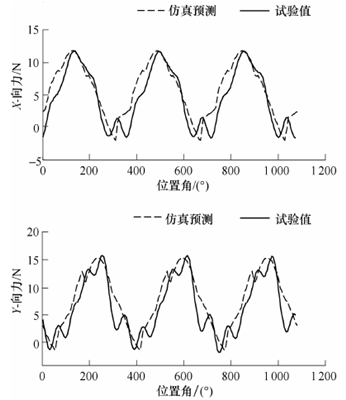
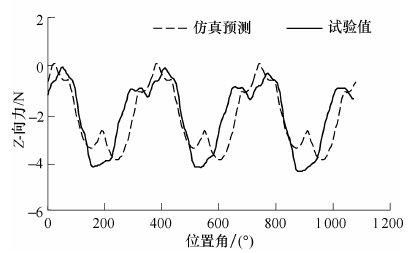
图16 基于新切厚计算方法的切削力预测结果与试验结果的对比
在不考虑刀具跳动的情况下, 4 刃铣刀的理论切削力周期应为90°。而且槽铣过程中,一般保持有2 个或者3 个齿同时参与切削,理论切削力不会为零。所以图15 所示的预测结果是合理的,但与试验结果不符。试验中所测切削力的周期为360°,说明试验中刀具跳动的影响是不可忽略的,传统不考虑刀具跳动的切厚模型难以运用在实际切削力的预测中。
图16 中切削力数据进行了低通滤波,滤波截止频率为850 Hz,略大于主轴转动频率的4 倍。因此,试验中所测切削力依旧保留着各齿切削的频率成分,加上实际中振动等干扰的存在,体现在波形上就可能出现一些小波峰或者非平滑跳动,图16中的Y 向力体现的特别明显。预测曲线由于考虑了多齿同时参与切削的叠加效应,各齿的力相叠加后也可能出现相应的波峰或者非平滑跳动区。考虑刀具跳动的情况下,每个齿的实际切削厚度都不相同,每个齿的切削力变化过程也必然不同,多个齿同时参与切削的过程中,其合力的变化周期应为360°。图16 中基于新切厚模型的切削力预测值与试验值的周期均为360°,很好地体现了这一特征。在考虑跳动下,某些刀齿的实际切厚要大于不考虑跳动的情况,其切削力峰值必然要大于无跳动的情况,所以图15 中出现预测值峰值小于实际试验峰值的情况。因此,基于新瞬时切厚计算方法的常用切削力模型,其预测切削力能更好地符合试验测量值。
5.结论
(1) 通过分析铣削过程中刀具的实际切削轨迹,建立了考虑刀具综合径向跳动下的适用于任意齿数刀具槽铣工况下的瞬时切厚计算模型,并给出了2 齿和4 齿情况下的具体计算公式。
(2) 分别讨论了刀具跳动和跳动角度对微铣削中各齿加工的影响,得出N=2 和4 时,刀具跳动角度分别为90°和45°有利于减小刀具跳动的影响。在与传统不考虑跳动计算方法的比较中,量化指出了刀具实际切入切出角的变化,以及铣削表面轮廓的改变,体现了微铣与传统铣削的不同。
(3) 通过与已有各解析法的比较,新方法优势不仅体现在适用于任意齿数下考虑刀具径向跳动的切厚计算,而且其精度可以与数值法相比的同时,没有计算上的稳定性问题,简洁的形式为编程计算提供了较好的选择。
(4) 在微铣削槽铣试验中,将新方法应用于刀具实际铣削加工的切削力预测,预测结果与试验结果相一致,体现了新方法的可靠性和实用性。目前在考虑跳动情况下的四齿铣削加工中,大多数都采用Newton-Raphson 等数值解法计算瞬时切厚。新方法的建立,有助于建立解析切削力模型,提升切削力模型的预测效果,从而有助于控制和优化微铣削加工工艺,提升产品的加工质量。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息




