轴承系统温度场分析
2014-3-21 来源:数控机床市场网 作者:洛阳轴承研究所 杨咸启
轴承系统的温升来自两个方面一是外部热量传入轴承之中,二是轴承自身摩擦发热。当轴承温度与其外界温度有差异时,轴承与外界的热量就要相互传递。轴承中的温度就随着这种生热和热交换而不断变化。当生热和交换热达到平衡时,轴承的温度就达到了稳定状态。轴承的温升与温度分布状态对轴承的性能 影响很大,它会影响轴承的安装配合,影响轴承的工作游隙,影响润滑剂的性能。温度升高会使轴承润滑状态恶化,导致轴承提前失效。因此对轴承系统进行热分析具有重要意义。它可以帮助合理地设计和正确地使用轴承,可以对轴承系统的故障和失效分析提供依据。
分析轴承温升需要将轴承、轴和座等作为统一系统来考虑。在这个系统中存在的散热形式有热传导、热对流和热辐射。在热对流中又包含有强迫对流和自然对流。因此这是一个很复杂的传热系统。以往对这种系统只能作一些简单分析。随着计算技术的发展,数值分析方法得到了广泛应用。如差分法〔有限元法川及边界元法阁等,但这些方法大都适用于单一形式的传热场合,如热传导。对于多种传热方式并存的场合应用这些方法往往有较大的困难。文献中介绍一种热流网络
交换法来分析轴承系统的温度分布。虽然此方法是一种近似法且只适用于稳态情况,但它可以考虑各种传热条件,并能得出与实际相符合的结果,因此得以应用。本文也将采用这种方法对轴承系统的温度场进行模拟。为此假定轴承系统的温度场是稳定的,它可以划分为一些具有不同温度的单元。对于每种单元可采用不同的传热模式,最后进行热平衡计算。根据这一模型开发程序,它不但可以分析单个轴承系统,也可分析包括轴、轴承和座这样多轴承系统的温度场。
一、热流网络原理
根据热流特性,当两点面间存在温度差时就会发生热流动。热流量可用下式来表达

(1)式可以描述所有形式的稳定传热过程。对不同的传热方式会有不同的表达形式。对于有多种温度区域的热流动也可应用(1)式进行热平衡计算。今设有区域 ,其温度为T,其中有热源发热率为Q,周边相邻区域的温度分别为T1、T2、T3和T4,见图1 。根据热流平衡原理,一个区域中热流流入量与流出量之差应等于该区域中的发热率。若规定流入的热量为正,流出的为负,则这一原理可表示为 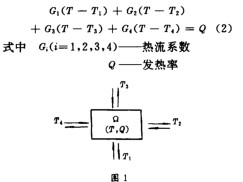 展开上式并整理后有
展开上式并整理后有 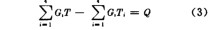
 展开上式并整理后有
展开上式并整理后有 上式可以推广到一般情形。设某一系统可分为N个温度区域,每个区域有M个热交换途径,系统共有M个独立的热交换路线,则在每个小区有 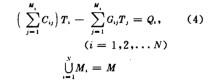
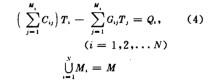
上述方程组中包含N个温度T及N个方程,将它们写成矩阵表达形式后有 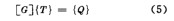
(5)式是系统整体热平衡方程,它表达了系统中热流网络之间的相互联系。当{G}和{Q}确定之后,即可求解这一方程组来获得系统的温度分布{T}。
为了能得到准确的温度结果,区域划分必须遵循一定的规则一是划分的小区域中的传热方式,要尽可能一致。二是小区域形状应尽量规则。三是系统环境温度需要当作一个温度点来考虑。对于轴承系统大都可划分为一些轴对称区域。
二、传热模型
在工程应用中,传热的形式及区域多种多样,对每一种区域都找出解析模型几乎不可能。但对几种规则的区域形状及传热方式,人们通过分析和试验已经建立起一些计算方法。而任何复杂的传热系统总可以划分为一些规则区域和传热方式组合,因此分析这些规则区域的传热是整个分析工作的前提。针对滚动轴承系统所涉及的传热模型已建立起多种计算公式,这里简介如下。
1 热传导
热传导可以分为平板导热、圆管壁导热和接触导热。这些形式的导热热流量的计算公式分别为 

2 对流换热
对流换热可分为强迫对流和自然对流。这些对流换热的热流量计算比较复杂,这里仅给出一般的计算公式,即 

4.轴承发热率
轴承中的发热 主要是由摩擦所引起的,而摩擦存在于所有接触处及流体搅拌中。计算这些摩擦力常用两种做法,一是通过轴承运动学、动力学分析来计算摩擦力。这种算法的结果较准确;另一种算法是以整体轴承来考虑,这就是palmgren经验公式,此算法比较简单,但结果是近似值。
(1)精确摩擦发热率分析
精确的摩擦力分析是建立在轴承运动学和动力学分析基础之上的。轴承中的摩擦大致可分为:滚动体与滚道接触处摩擦、滚动体与保持架摩擦、滚子与轴承挡边摩擦、滚动体与流体间搅拌摩擦和保持架搅拌阻力等。这些摩擦发热率的一般计算式可写为 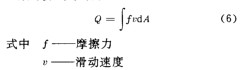
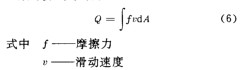
(2)近似摩J察发热率分析
palmsren根据试验结果建立起一组摩擦力经验公式,根据这些公式可以近似计算出摩擦发热率 


三、热流网络模拟与方程求解
根据以上分析原理,可实现计算机热流网络模拟。首先按轴承系统的温度分布特点,将其分为一些温度小区域,对每个小区域进行编号,由小区域间热流的传递方式来确定网络形式。
为便于计算机实现,定义了两个二维数组,它们分别代表热路性质及有关计算参数。数组ITG规定了热路的形式,ITG(i,1),ITG(i,2)为热路两端点的节点号ITG (i,3 )为热路性质。数组GEZ规定了热路上的有关特征参数。这样规定以后,程序就可自动生成热路平衡方程(5)。它是一组非线性方程,求解这类方程有很多方法。本文采用高斯迭代法和布 罗登迭代法。在节点数比较少的情况下采用高斯迭代法比较经济,对于较多的节点问题,布罗登法比较优越。具体的模拟计算过程可参阅文献 [12)。
四、程序介绍与计算结果。
1.程序框图
根据上面介绍的模型开发了sYBTEM程序,其框图见图2。
2.计算结果利用
程序SYBTEM 分析计算了球轴承系统的温度分布。它是以航空发动机主轴轴承寿命考核试验条件来确定的。试验中对一些关键的温度进行了测定,计算结果与此进行了对比,下面给出具体的结果。此系统的热路网络如图3所示。
试验轴承为两套。
轴承代号为:D1276720QKIT2
轴承结构尺寸:D=165,d=100,
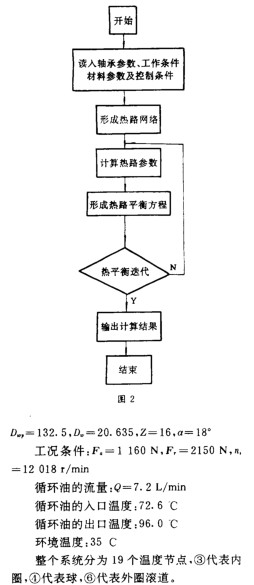
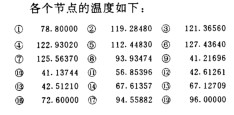
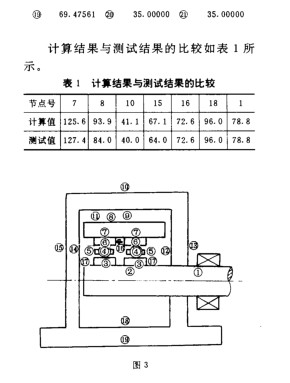
五、结论
本文利用热路网络热流量平衡原理来分析轴承系统的传热,系统可以同时包含:热传导、热对流和热辐射。对系统的结构形状没有特别要求,因此它适用各种工程传热场合。在计算系统温度场时,只需确定各热路性质、发热率和环境温度。程序可自动计算出各节点上的温度值。热流网络可手工生成,也可实现自动生成。实例分析结果表明:计算结果与试验值是吻合的。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com




