宏程序车削异形螺纹的编程探索
2020-6-4 来源: 桂林航天工业学院 实践教学部 作者:朱治法 孙艳华 杜春平
摘要:探讨使用 FNAUC-Oi数控系统车削异形螺纹时宏程序的应用。选择手工编制加工程序,合理优化参数设置成变量,并赋值,再进行数学计算、逻辑判断和程序运行跳转功能,解决简化编程,实现分层左右借刀车削减少车刀单刃车削磨损严重和容易产生的“扎刀”现象。
关键词:异形螺纹;宏程序;简化编程
宏程序作为数控加工程序编制的高级形式,其程序编辑具有较大的灵活性,程序的使用具有较好的通用性,程序结构与内容具有较高的智能性等特点[1]。宏程序可以实现子程序的功能甚至能完成二次及多次曲线加工的特殊功能。在螺纹加工方面,宏程序应用在车削梯形螺纹、矩形螺纹、蜗杆和牙型异形且牙型深度较大的螺纹编程中优势突出。比如在车削大螺距螺纹时可实现左右借刀车削,车刀受力均匀,避免车刀单刃车削磨损严重等问题。若单独应用螺纹车削指令加工比较困难,在加工程序书写上不仅编辑工作量大,而且容易出错。本文探索在程序中使用变量配合螺纹固定指令来编程加工数控加工,优化加工程序和解决车削难题。
1、异形螺纹编程分析
1.1 螺纹车削指令
FNAUC-Oi系 统 数 控 车 床 给 用 户 提 供 了G32、G34、G76、G84、G92五个螺纹加工指令,可满足用户完成普通公制、英制螺纹的加工,其加工特点如表1所示。
表1 螺纹车削指令

这些螺纹车削指令在切削用量等方面各有特点,但是单一使用螺纹加工指令编写螺距较大和牙形深度较大的异形特殊螺纹时,在编程书写上存在编辑工作量大且容易出错的情况。当用宏程序编辑加工程序时,可以把螺纹总切深和z 方向的加工余量用变量来表示。利用宏程序的数学运算和逻辑判断来确定加工时切削用量和切削次数,实现分层车削和左右借刀车削。在编制加工程序时,将加工指令 G92与宏程序灵活地结合起来,可以有效地简化编程、合理控制、优化切削参数。
1.2 异形螺纹
异形螺纹是指螺纹的轮廓以及牙型与普通螺纹存在明显差异,其主要包括惠氏螺纹、ACME 英制梯形螺纹、锯齿形螺纹、圆螺纹、方牙螺纹、API螺纹、圆弧螺纹、梯形螺纹、变距螺纹等[2]。对于异形螺纹的加工,若单独利用螺纹指令加工,在切削深度、左右借刀车削等方面需要进行大量的切削起点计算,重复工作量大。
2、异形螺纹加工编程
如图1所示的异形螺纹,其毛坯为:φ52mm×152mm
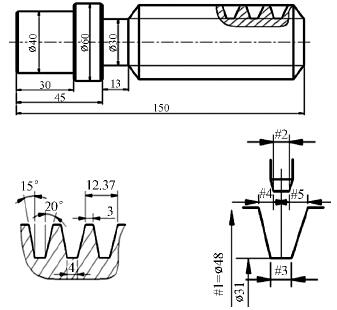
图1 异形螺纹轴(单位:mm)
2.1 工艺分析
2.1.1 刀具的确定
通过分析图1可以看出此螺纹牙型是左侧半角为15°,右侧半角为 20°的异形螺纹。由于螺 纹牙型形状比较特殊,常见方法是采用成型刀具来加工[3]。本文中实例车削加工时螺纹两侧面半角是由角度参数引导形成的,在保证车刀有足够的强度下刃磨出较大的螺纹升角。为了能获得螺纹两侧面较小表面粗糙度值,车刀刀尖部分可以刃磨成左右两侧稍小于牙型半角的形状。车刀几何角度的正确选择,可以大大改善车削效果,保证稳定的加工质量,顺利完成螺纹加工[4]。
2.1.2 装夹方式
在加工中要保证工件的装夹强度,避免出现振动和位移现象。在此选择“一夹一顶装夹”方式装夹工件。工件左侧φ40mm×30mm 的圆柱作夹位,在工件右端面中心处钻 A5 中心孔,利用活动顶尖支承。
2.1.3 编程分析
宏程序在应用过程中其结构根据所使用的循环语句和 判别方 式灵活安 排。变 量确定、变量赋值、变量运算、程序跳转等语句在用户宏程序本体中使用时,编程人员需要综合分析宏程序,设计合理的工艺路线,合理提取变量,以便制定出符合产品的加工程序,设计的编程思路如图2所示。
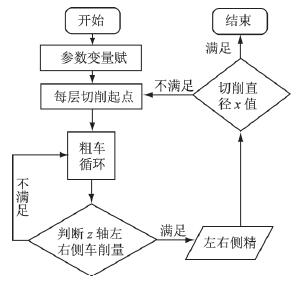
图2 编程思路
粗精车完成图1中各外径尺寸和切槽部位表面。采用一夹一顶方式装夹工件,建立工件坐标系零点在工件右端面中心处,直接编写螺纹部分加工程序。宏程序中变量的设置是核心内容,要做到变量设置尽量少。利用宏程序编辑螺纹加工程序,最主要是解决分层车削和左右多次车削,加强对刀具的精确控制。实现分层车削只需设定大径为变量与螺纹小径进行数学 运 算和逻辑判 断即可实 现。利用 G92螺纹循环车削指令实现左右多次车削,只需将切削起点进行数学计算,左右相应移动即可以完成控制。
2.1.4 变量赋值及分析
变量赋值如表2所示。
表2 变量赋值

设置第一层切削直径尺寸在螺纹大 径φ48处,参考计算点在刀头横刃中点位置,刀头宽度3mm。计算第一层左侧借刀偏移量约为#4=2-#2/2+TAN[15]*[[#1-31]/2]=2.77 mm。左侧偏移借刀量为0.3mm/每刀,2.77/0.3=9.23刀,共借刀十次,第九刀车削完成后,根据判别公式最后一刀左侧吃刀量为0.07mm。螺纹刀右侧偏移总量#5=2-#2/2+TAN[20]*[[#1-31]/2]=3.59mm。右侧偏移借刀量为0.4mm/每刀,3.59/0.4=8.975刀,共借刀九次,第八次车削完成后,根据判别公式最后一刀右侧吃刀量为 0.398mm。第一层切削总刀数为:第一次切削+左侧总借刀数+右侧总借刀数共20(1+10+9=20)次。每层切削次数根据切削直径变化而定,直径方向切削每层变化0.5mm,(48-31)/0.5共分34层,总切深(48-31)/2=8.5mm。
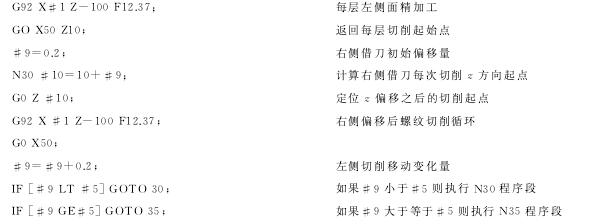
3、加工程序
加工程序如表3所示。
表3 FNAUC-Oi系统



4、结束语
在数控加工程序中可以有效地利用变量、数学运算和逻辑判别表达一个循环体,本文中列举的数控加工程序极大地缩减了未使用变量编程的加工程序,在实际加工过程中有效地缩短了手工编程时间,提高了车削效率。其步骤如下:
1)设置螺纹大径为变量并赋值,在直径方向与切削深度进行数学运算,得出运算结果与螺纹底径做循环判断,从而实现直径方向每层车削的循环。
2)根据螺纹车刀刀头宽度计算出第一层车削左右车削总余量,分左右两边设置偏移量进行数学运算,移动量与每层左右车削总余量进行判别,实现每层左右车削。
3)螺纹牙型角度由数学公式计算,参数引导得出。在表面加工精度和质量上有待尝试采用新工艺解决。
在程序运行车削过程中,零件加工表面粗糙度方面并不是太理想,为了改善加工精度和表面粗糙度,还应从刀具和更优化的切削参数等方面探索有效的精加工方法。使用宏程序缩减优化螺纹加工程序对特异形螺纹车削加工有重要的意义。针对在螺纹牙型类似但尺寸不同的螺纹加工中刀具轨迹相同的问题,车削加工时只需改变位置参数和相应变量参数便可获得其加工程序。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息





