数控机床三维空间几何误差补偿方法
2018-6-5 来源:南京航空航天大学 机电学院 作者:朱建伟,陈蔚芳,郑德星,朱赤洲
摘要: 为了提高数控机床的加工精度,在系统分析数控机床几何误差常用补偿方法基础上,提出了基于数控系统插补数据的几何误差补偿方法,并将误差补偿功能集成于国产数控系统中,以提高国产数控系统的综合性能。通过实验与仿真结果表明,数控系统插补数据的几何误差补偿方案能显著提高数控机床的加工精度。
关键词: 数控机床; 数控系统; 误差补偿; 机床精度
0、 引言
随着机械制造业的不断发展,精密加工已逐渐成为现代制造业的主要趋势,误差补偿技术也因此获得了迅速发展。误差补偿有硬件补偿和软件补偿2种补偿策略。硬件补偿专用性比较强,在国内外都没有得到较好的发展;而软件补偿则通用性较强,国内外有很多学者对其进行了研究。Y.Y. Hsu 和 S.S. Wang 等人提出了一种新的五轴机床误差补偿解耦方法,分别计算出机床转动轴和移动轴的误差,并应用于机床后置处理中,获得了优化的NC程序; Ibaraki 等提出多轴机床几何误差测量新方法,并完成误差补偿; Feng Huo 等人在系统的研究了影响轮廓铣削加工精度影响因素的基础上,分析了各因素的补偿方法,并实验验证了补偿方法的可行性; 在国内,何振亚在研究 PMAC 卡的运动误差补偿功能中,用 Matlab 实现了对机床空间误差的可视化分析及补偿。王维等人提出了一种包含几何误差与热误差的综合误差建模方法,采用数控系统的坐标偏置命令,进行实时在线补偿,取得了较好的效果; 韩飞飞等人利用机床几何误差分析法,通过激光干涉仪检测机床各项误差,发现了各个运动轴及某一轴的不同工作区间误差规律,由此提升机床加工精度。
目前国内大多数数控机床空间误差补偿方法都很难与数控系统真正集成,仅是简单地将误差映射给加工过程,补偿效果不够理想。因此,有必要将空间误差补偿功能嵌入到数控系统中,实现与数控系统的集成,提高其实用性、实时性和可靠性。
文中系统研究了数控机床三维空间误差补偿方法,着重研究了不同补偿方法的工作原理,提出了基于数控系统插补数据的误差补偿方法,有效提高了数控机床精度。
1、 数控机床三维几何误差补偿方法
常见的数控机床三维空间误差补偿方法主要有以下几种。
1) NC 代码修正补偿法
在数控机床误差的影响下,如果按照理想的 NC 代码对零件进行加工则存在加工误差,为了消除数控机床误差对加工过程的影响,可以对 NC 代码进行修正,用修正后的数控加工程序对工件进行加工,从而实现数控机床误差的补偿。补偿流程图如图 1 所示,将 NC 代码输入到误差补偿软件中,然后生成理想刀具路径,并根据误差补偿预测模型对理想刀具路径进行修正,得到实际的刀具路径轨迹,最后生成修正后的 NC 代码。该方法对数控机床几何误差的补偿具有良好的效果。
2) 接口式 NC 型误差补偿法
接口式 NC 型误差补偿方法是将由误差预测模型计算得到的误差值,叠加到数控系统的插补过程。基本工作原理如下: 通过特定的误差补偿接口,NC 系统将当前机床的各项参数( 机床位置参数和刀具信息等) 传递给误差预测模型,经过误差预测模型计算出相应的误差值反馈给NC 系统,NC 系统对误差值进行处理,生成新的数控程序,实现误差的补偿。如图 2 所示。
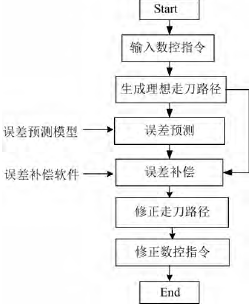
图 1 数控加工指令修正补偿示意图
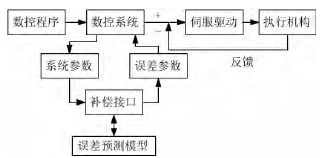
图 2 接口式 NC 型误差补偿示意图
2、 基于数控系统插补数据的误差补偿方法
在接口式 NC 型误差补偿方法的基础上,提出了一种基于数控系统插补数据的数控机床三维空间误差补偿方法。这种补偿方法是基于数控系统的动态补偿,它将数控机床三维空间误差融合到数控系统中,通过外部开发补偿软件修正数控系统中的粗插补数据达到对数控机床三维空间误差的补偿目的。补偿流程如图 3 所示。
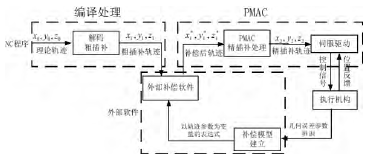
图 3 基于数控系统插补数据的补偿方法
外部补偿软件可以补偿几何误差和热误差。数控机床的几何误差是一种准静态的误差源,具有一定的静态特性,在某一环境温度范围内可视为常量,较为容易与数控系统集成实现其误差的实时补偿; 而对于高精度的数控机床,热误差是最大误差源,占机床总误差的 40%以上。热误差模型的建立和机床的结构是密切相关的,通常采用在机床的关键点布置温度测量传感器,采集得到相应的敏感点温度,最后通过相应的误差模型计算出误差值,对加工过程进行实时的补偿。
外部补偿软件获取和修正数控系统数据流的前提是数控系统应提供一个数据接口实现与外部软件的信息交互,因此需要进行数据接口的编写。此外,在实现误差补偿功能时外部补偿软件和数控系统应同时运行,操作起来比较复杂,工作效率相对较低。考虑到这些因素后,作如下改进处理,即将外部补偿软件作为一个模块嵌入到数控系统当中,以此提高数控系统的智能化和集成化程度。
上述补偿方法是 NC 型误差补偿法的一种特殊类型。该方法相对于 NC 代码修正补偿来说有很大的优点,机床的参数可以直接在数控系统的数据流中提取,并且经过进一步的处理可以将误差模型、误差元素等以配置文件的方式引入数控系统,通用性较好。此外,与传统的基于数控系统的硬件补偿方法不同,该补偿方法不采用硬件接口,不需要引进相应的硬件设施,而是通过软件接口进行通信实现各项功能,可靠性更高。
基于数控系统的补偿方法相对于 NC 代码修正补偿来说有其独特的优越性。假定 2 种补偿方法的加工条件一致,下面具体分析 2 种补偿方案的补偿精度。
基于 NC 代码修正的补偿,其补偿值反映在 NC 加工文件中的坐标点上。在 NC 文件中,每一行代码中的坐标点都是该段直线( 圆弧) 的终点,同时也是下段直线( 圆弧) 的起点,采用这种补偿方式只是对每段线的起点和终点的修正,没有考虑中间点的误差,在执行 NC 文件时采用误差均匀化的方法折合成该点的误差量。基于数控系统的嵌入式补偿,在数控系统的数据流中反映补偿值,该数据流是对 NC 文件实施预处理、刀补、轨迹规划等一系列操作后的细密数据,能尽可能多的考虑到加工过程中的数据点。如图 4 所示,xy 平面( G17) 上的半圆弧为例,其中点( x0,y0) 代表圆弧的圆心位置,点( x1,y1) 代表圆弧的起点,点( x2,y2) 代表圆弧的终点位置,R 代表圆弧的半径,( x0’,y0’) 和( x2’,y2’) 代表补偿后的圆弧圆心和终点坐标。图4(a) 是基于 NC 代码修正的补偿,由图可知每段代码只是补偿该段代码的终点; 图 4( b) 是基于数控系统的补偿,由图可知补偿位置点细密,考虑到了圆弧中尽可能多的位置点。
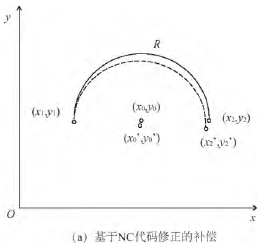
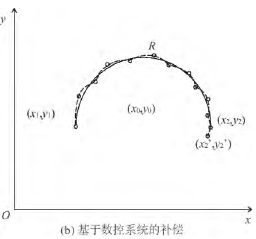
图 4 2 种补偿方法的对比
综合上述的分析,可知 2 种补偿方案都具有各自的特点,如表1所示.
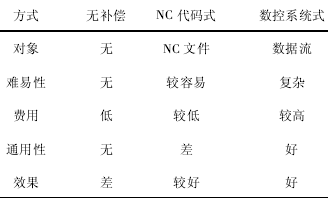
表 1 误差补偿方法的比较
3 、基于 SKY 数控系统的实验验证
SKY 数控系统是基于 PMAC 运动控制卡的开放式数控系统。对文中提出的误差补偿方法的补偿效果进行验证,设计了实验方案以验证所提出的补偿方法的有效性。
a) 实验方案设计
为了达到验证误差补偿方法有效性的目的,实验方案设计如下: 实验对比环境需要有 2 组,一组为无补偿与软件式补偿的对比,另一组为无补偿和数控系统式补偿的对比。
为了尽量避免外部因素的影响,实验不进行零件的实际加工,以免引入切削力引起的误差; 由于机床各个轴系的运动均能反映误差补偿方法的有效性,为了简化工作量,仅对单轴方向的线性误差进行测量。同时考虑到误差检测的可靠性和准确性,实验选取激光干涉仪检测机床线性误差。
b) 实验条件和实验步骤
实验的对比环境分为 2 组,为“无补偿+软件式补偿”和“无补偿+数控系统式补偿”; 实验的待检测机床为具备上述对比环境的 SKY-DX70100 型数控机床; 检测的目标数据为机床 x 轴向的线性误差; 误差检测仪器为雷尼绍激光干涉仪。
激光干涉仪检测 x 向误差时,需要驱动机床沿 x 向在固定范围内往复运动。误差检测时的数控程序如下:
G92 X0 Y0 Z0;
M98 P100 L11;
M98 P200 L12;
M98 P100 L12;
M98 P200 L12;
M02;
: O100
G90 G00;
G91 G00 X-50;
G04 X3;
M99;
: O200
G90 G00;
G91 G00 X+50;
G04 X3;
M99;
其中: G92 为坐标系设定指令; M98 为子程序调用指令,P 表示调用的子程序编号,L 表示调用次数; G04 为等待指令,X 的数值表示等待的时间; : O100 和: O200 为子程序编号; M02 表示程序结束,其余指令的功能与标准数控代码一致。
实验步骤如下:
1) 分别在不进行机床误差补偿、采用软件式补偿策略和采用数控系统式补偿的条件下,采用激光干涉仪对指定数控机床的 x 轴向线性误差进行测量,测量结果分别为X_Data1.rtl、X_Data2rtl、X_Data3.rtl 文件;
2) 验证补偿策略的有效性;
3) 实验结果分析和讨论。根据测量结果 X_Data1.rtl、X_Data2.rtl 和 X_Data3.rtl,可以得到未补偿时机床 x 轴向的线性误差范围为( -76.0μm,8.6 μm) ; 采用补偿软件后机床的 x 轴向线性误差范围为( -10.8 μm,-2.0 μm) ; 补偿功能与数控系统集成后机床的 x 轴向线性误差范围为( -6.8 μm,1.1 μm) 。根据 GB/T17421.2-2000 标准分析测量结果 X_Data1.rtl、X_Data2.rtl 和 X_Data3.rtl,得到该机床 3 种条件下的 x轴向线性误差曲线如图 5、图 6 和图 7 所示。对比图 5 和图 6 可知,相对于未补偿时的 x 轴线性误差曲线,采用误差补偿软件后,线性误差的范围大大缩小,由原来的 84.6 μm 减少到 8.8 μm,降低了 89.6%。对比图5 和图 7 可知,当补偿功能与数控系统集成后,x 轴的线性误差曲线的误差范围也大大缩小,由原来的 84.6 μm 减少到 7.9 μm,降低了 90.7%。几种补偿条件下 x 轴线性误差相关参数的比较如表 3 所示。
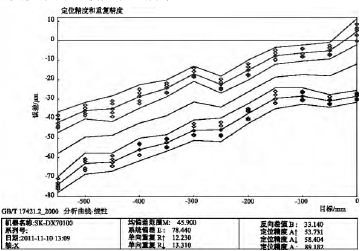
图 5 无补偿条件下机床 x 轴向线性误差图
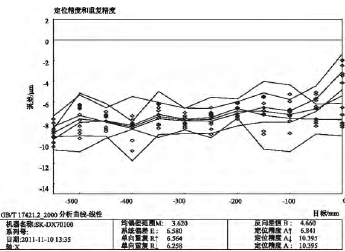
图 6 软件式补偿条件下机床 x 轴向线性误差图
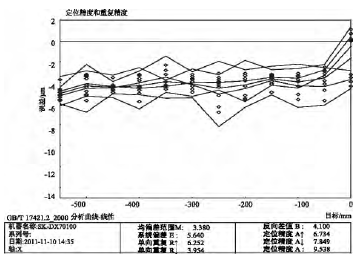
图 7 数控系统式补偿条件下机床 x 轴向线性误差图
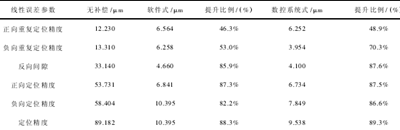
表 3 不同补偿时 x 轴线性误差分析表
根据上述分析可知,采用基于补偿软件与数控系统通信的补偿方法和补偿功能与数控系统集成的补偿方法都大幅度降低了机床的 x 轴向线性误差,因此,论文提出的补偿方法能有效地提高机床的性能。
4 、结语
通过对数控机床常用的空间误差补偿方法进行分析,提出了一种基于数控系统插补数据的误差补偿新方法,实现误差补偿功能与数控系统的集成。根据实验结果可知,采用补偿软件与数控系统通信的补偿方法、补偿功能与数控系统集成的补偿方法均能大幅度改善机床的性能,为设计开发精密数控机床提供了一条可行的路径。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息





