车床主轴与进给轴耦合热误差建模及补偿研究
2015-11-23 来源:数控机床市场网 作者:西安交通大学机械制造系统孙志超陶涛黄晓勇
孙志超,陶涛,黄晓勇,梅雪松,王新孟,杨军,赵亮
(西安交通大学机械制造系统工程国家重点实验室,710049,西安)
摘要:针对车床实际加工中主轴与进给轴的热误差相互耦合共同影响工件精度的问题,建立了综合热误差模型,并进行了有效补偿。以海德曼 HTC500/500 精密车床为研究对象,对车床主轴与进给轴热误差的耦合关系进行了解耦。利用模糊聚类理论实现了车床测温点的优化分组,建立了主轴与进给轴的耦合热误差多元线性回归模型,并在精密车床上得到实际应用。结果表明:车床耦合热误差模型符合实际工况,模糊聚类有效降低了温度变量之间的多重共线性,提高了模型的预测精度;主轴x/z方向热误差模型预测精度达88.4%、90.7%, x/z轴热误差模型预测精度达82.9%、71.3%;补偿后车床 x/z 方向精度分别提高了60.3%和 56.6%,证明耦合热误差模型的准确性。
关键词:热误差解耦;热误差建模;模糊聚类分析;误差补偿
机床热误差严重制约着精密和超精密加工行业的发展,热误差占据了机床总误差的 70%,对机床的加工精度影响最大。目前,消除热误差主要有两种方法:热误差预防法和热误差补偿法。近年来,对机床热误差方向的研究越来越多,相关方面的理论也越来越多,产生了很多有价值的科研成果。Donmez 认为变化的温度是机床产生热变形,是机床的主要误差源,机床越精密受其影响越大;Mou 认为机床的热特性是由于热源位置、机床材料及强度、机床结构等多种因素共同作用相互耦合作用的结果;Min 等人提出了基于傅里叶热力学方程为基础的热态模型,分析不同边界条件下丝杠温度场的分布特性,对研究机床进给轴热误差特性打下一定的基础。相关理论的增多也伴随着机床热误差建模方法的增多,Yang等人利用神经网络技术建立了主轴热误差与温度之间的关系模型;杨军等人利用模糊聚类优化温度测点,并结合最小二乘支持向量机和神经网络技术,构建了精密坐标镗床主轴的热误差模型,取得了良好的预测效果;Wu 等人利用有限元仿真技术,建立了丝杠预紧力和进给速度与丝杠温度场和热变形的关系模型,并通过试验验证模型的有效性;Lin 等人利用最小二乘支持向量机理论建立了主轴热误差与温度变化的相关关系;郭前建等人结合聚类分析理论建立了滚齿机热误差的多元线性回归模型,提高了热误差模型的预测精度。Chao 等人利用 BP 神经网络模型和基于反馈线性自回归滑动平均的小波元神经网络模型建立了数控机床进给系统在不同工况下温度场分布和热变形的数学模型;谢春等人利用 BP 神经网络算法建立了五轴车铣复合加工中心进给轴的综合热误差模型,并做了相关实验验证;Abdulshahed 等人提出了一种改进的自适应模糊推理系统(ANFIS),建立机床主轴的热误差预测模型,提高了预测精度;苗恩铭等人建立了数控加工中心主轴的支持向量回归机模型,并在不同的环境温度下验证模型的准确性,均取得了良好的预测效果。
当前文献主要针对机床的主轴和进给轴单个系统分别进行建模及补偿,而实际加工中主轴与进给轴的热误差是并行存在,共同影响工件的加工精度。单个系统独立补偿与实际不符,而将两者的热误差结合在一起的研究非常少。本文针对机床主轴与进给轴热误差的耦合问题,进行了解耦分析,建立了耦合热误差模型;并以海德曼HTC550/500 车床为研究对象,进行了补偿应用,验证了耦合热误差模型的有效性及鲁棒性。
1 Siemens 系统热误差补偿方法
1.1 Siemens 热误差补偿方式
为了适应市场需求,西门子为用户提供了热误差补偿的接口,供用户自定义热误差补偿的形式及模型参数。西门子认为金属受热膨胀与温度之间是线性关系,主轴的热误差模型只与温度有关,与坐标位置无关;进给轴的热误差模型则与温度和坐标位置都相关。西门子开放的热误差补偿方式如图 1 所示。

1.2 主轴与进给轴热误差解耦
机床的热误差最终反映在刀具与工件相对位置的偏离,从而导致机床的加工精度降低,废品率升高造成生产成本的提高。热误差补偿的目的就在于消除或者减小由于金属热膨胀而导致的机床刀具与工件之间的位置偏离,从而提高机床的加工精度。刀具与工件之间位置的偏离本质上是由于主轴与进给轴热误差相互耦合共同作用的结果,因此寻找主轴与进给轴之间的耦合关系对于热误差模型的建立至关重要。为了能够得到准确的热误差数学模型, 就需要对两者之间进行解耦,分别得到各自的数学模型,再将模型根据耦合关系耦合在一起,便得到了机床总体的热误差数学模型。
进给轴在进给状态下丝杠螺母副由于摩擦产生热量,丝杠温度升高,伴随着热伸长。此车床是半闭环系统,丝杠的伸长导致进给轴热误差的产生。主轴在高速状态下旋转时,前端轴承与后端轴承由于摩擦产生一定的热量,热量传递到主轴,主轴受热就会产生热变形,导致热误差的产生。主轴热伸长 l的方向 z 轴相同,而主轴热升高 h则会在 x 轴方向产生分量 x。只有分别分析主轴和进给轴的热误差,分别建立相应的数学模型,才能准确全面的反映车床在 x、z 方向产生的热误差。主轴与进给轴的热误差耦合示意图如图 2 所示。
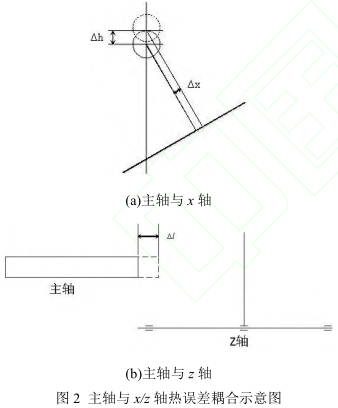
车床主轴只有旋转一个运动状态,不存在坐标位置的变换,故主轴的热误差只与自身温度变化相关,热误差模型与位置无关。环境温度的改变,以及主轴由于旋转造成自身温度的提高,不仅会影响主轴的热伸长,同样会造成主轴在垂直方向的变化。主轴在垂直方向位置的变化主要是由于主轴箱体受热膨胀导致主轴整体升高,受环境温度影响较大,主轴在 x 方向的热误差多元线性回归模型可以表示为

x 轴的热误差主要是由 x 轴丝杠的热伸长引起的,丝杠的固定方式为一端固定一端游动,靠近电机端为固定端,远离电机端为游动端,当 x轴丝杠受热时会向游动端伸长,固定端位置不会发生变化,可以作为热误差为零的参考点。x 轴热误差与位置和温度相关,选定参考点,x 轴的热误差多元线性回归模型可以表示为

以上将机床 x 方向的热误差分别解耦到主轴和 x 轴各自的热误差,并分别建立了各自的热误差模型。解耦是将复杂问题简单化,解耦之后还需要解耦后的结果重新进行耦合。x 轴为倾斜式安装,如图 2a 所示,机床 x 方向热误差的耦合模型为

同理,主轴的热伸长与 z 轴方向相同,热误差多元线性回归模型可以表示为

2 热特性实验及结果分析
2.1 实验设计及测量原理
以浙江海德曼机床有限责任公司生产的HTC550/500 车床为研究对象,分析车床 x、z 方向热误差与温度变量的关系。车床 x 和 z 方向的最大有效行程分别为 180 mm 和 520 mm,最高进给速度分别为 30 m/min 和 36 m/min。
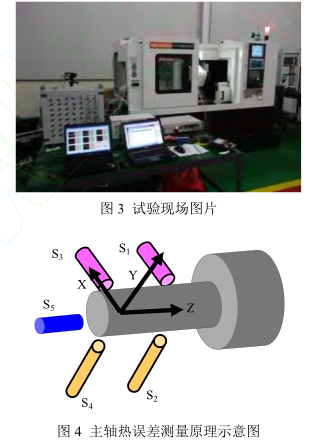
测试设备如下: RENISHAW 激光干涉仪用于测量进给轴热误差值;温度位移同步采集系统获得温度值及主轴热误差值;选用高精度温度传感器 PT100、高精度电涡流位移传感器。温度传感器 PT100 记为:T1…T17,T1~T8安装在主轴箱前端、后端和中部,T9z 轴电机,T10z 轴前轴承,T11z 轴后轴承,T12z 轴螺母座,T13x 轴电机,T14x 轴前轴承,T15x 轴后轴承,T16x 轴螺母座,T17 环境温度;位移传感器记为:S1,…,S5。试验现场和主轴测量原理如图 3、图 4 所示。 以机床主轴、x/z 轴的热误差为研究对象,主轴的热误差测量采用五点法测量,如图 4 所示。主轴的热伸长有 S5测量获得,x 方向的热误差由S1和 S3测量获得,y 方向的热误差由 S2和 S4测量获得。由于转速不同,主轴的热变形略有不同,实验中设计了 1 000、1 500、2 000 r/min 3 种不同的转速。 z 轴热误差由激光干涉仪进行测量,测量范围为[-495,0],各测量点间距为 45 mm,共 12个测点。z 轴坐标 0 处作为激光干涉仪测量原点。x 轴的热误差测量范围为[-165,0],各测点间距为15 mm,共 12 个测点,0 处作为激光干涉仪测量原点。试验初始时,在冷态下测量进给轴各测点误差,作为进给系统的几何误差,进给系统连续往复运动 30 min 后测量各测点的误差值,此误差值减去几何误差作为此刻进给系统的热误差。依据 VDI/ISO 标准,每次重复测量 3 个循环,每个测点测量 2 s,进给系统暂停 4 s,为防止反向间隙对端点出热误差产生影响,取反向越程 5 mm。由于进给速度不同,进给系统的热变形略有不同,实验设计了 500 mm/min、1 000 mm/min、1 500 mm/min。
2.2 结果分析
2.2.1 温度场时域分析
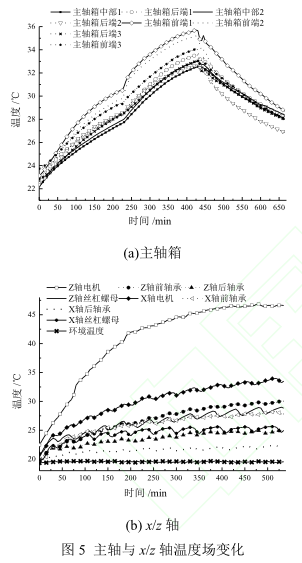
当主轴旋转进给轴不动时,主轴箱的温度变化如图 5a 所示。主轴箱前端最高温度达 36℃,最大温差大约 13℃;主轴箱后端最高温度达 34℃,最大温度差 12℃;主轴箱中部最高温度达 33℃,最大温差 11℃。由主轴的结构可知主轴前端有一个圆柱滚子轴承和两个角接触球轴承,后端一个圆柱滚子轴承,主轴箱内部有空隙。主轴箱前端生热较多,后端生热较少,所以主轴箱的温度场分布如图 5a 所示,前端温度高于后端,中部温度最低。
当 z 轴进给主轴不动时,z 轴丝杠螺母座与电机端轴承的温度变化如图 5b 所示。由于丝杠为转动体,无法用 PT100 直接测量丝杠的温度,因此改为测量丝杠螺母座和电机端轴承座的温度来间接反映丝杠的温度变化,这是由于丝杠温度的变化是由轴承及丝杠与螺母之间相对转动产生摩擦而发热,引起温度的变化。因此,由螺母座和电机端轴承的温度来间接反映丝杠的温度变化是合理的。同理,当 x 轴进给时机床其他部分静止,x轴丝杠螺母座与电机端轴承的温度变化如图 5b所示。
2.2.2 主轴热变形分析
主轴的内部结构如图 6a 所示,由图可看出皮带轮带动整个主轴系统的运转,主轴为中空轴,有循环空气进行冷却,主轴前端有三个轴承后端一个轴承,主轴的中部与主轴箱之间有空气间隔。主轴旋转时轴承的内外圈与滚子之间相对运动产生摩擦而发热,热量通过热传导分别传递到主轴、主轴箱体下部及主轴箱的其他部分。主轴温度的升高是导致主轴热伸长的主要原因,而主轴的热伸长导致机床 z 方向产生热误差 Z;主轴箱体下部的温升是导致主轴整体升高 h的主要原因,而主轴的整体升高导致机床 x 方向产生热误差x。 x由 S1、S3测量得到,取其平均值作为 x热误差值。
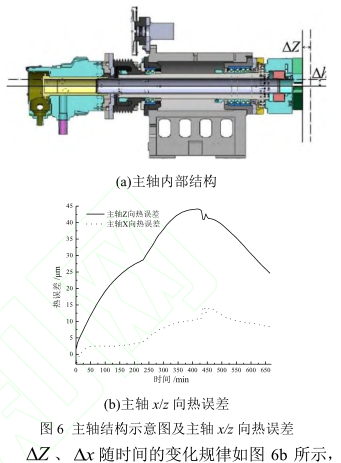
其变化规律与图5a主轴箱温度变化规律基本保持一致。这就说明主轴的热变形与主轴箱温度之间存在者密切的关系:随着主轴箱温度的升高,主轴的热变形随之增大,当温度最高时主轴的热形达到最大值;主轴停止旋转后主轴箱温度逐渐下降,主轴的热变形也随之减小。S1/S3的采集值偏差较大,这说明主轴在径向产生了偏摆,本文忽略了主轴在 x/y 方向的摆角问题。
2.2.3 进给轴位置相关热误差分析
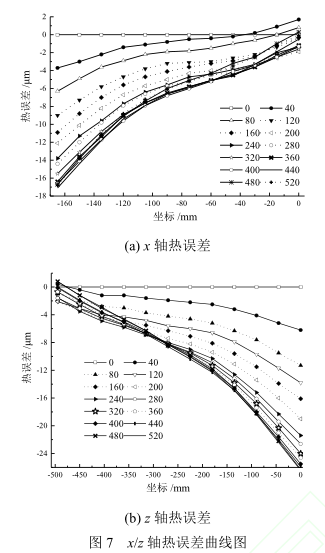
进给轴 x、y 具有同样的结构形式,两端分别为固定端和游动端。当进给系统运动时,电机、轴承、丝杠螺母副生热,导致进给轴丝杠受热膨胀,固定端位置不变,游动端向自由方向伸长,进给轴在本实验中的热变形如图 7 所示。
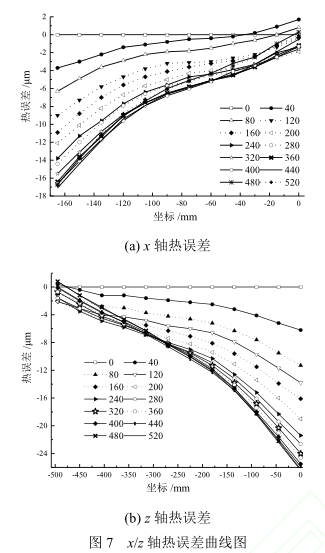
在冷态下第一次测量误差作为机床的几何误差,即第一次冷态测量时各测点的热误差为 0,图 7 说明各次测量的时间间隔,由图可以看出,进给轴的热误差与位置相关,两者之间近似成线性关系,且热误差随坐标位置的增大而增大。进给轴的固定端热误差变化相对较小,而游动端热误差变化相对较大,说明车床进给轴位置坐标距离电机越远,定位精度越低,热误差越大,这种变化规律符合丝杠的结构形式。电机端为丝杠的固定端,远离电机端为丝杠的游动端。
3 热误差建模及补偿实现
3.1 温度测点优化
3.1.1 模糊聚类分组
利用模糊聚类分析方法对温度变量进行分


3.1.2 基于相关分析的温度测点筛选
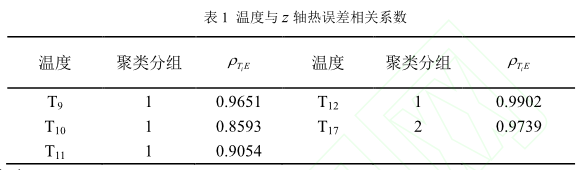
依据上述模糊聚类分组结果,应用统计学相关性理论进行测点优化,求取Ti与热误差 E 的相关系数为

的平均值;iE 为热误差的平均值。相关系数如表1 所示,选择每个聚类分组中相关系数大的温度作为典型变量。故选择 T12,和 T17为典型温度变量。
以上介绍是以其中一项热误差为例,实际中热误差包括主轴热伸长、主轴热升高、x 进给轴热误差及 y 轴进给轴热误差,在进行模糊聚类时需要针对不同的热误差项分别进行聚类分组,得到与各个误差项最相关的典型温度变量。
3.2 热误差模型
温度变量优化之后可以进行热误差数学模型的建立,主要有 BP 神经网络法、支持向量机法、多元线性回归等,本文以多元线性回归模型为例。基于多元线性回归模型及实验数据,可得到热误差的数学补偿模型。分别建立机床主轴 x 向热误差与 z 向热误差、x 进给轴及 y 进给轴的热误差补偿模型,即

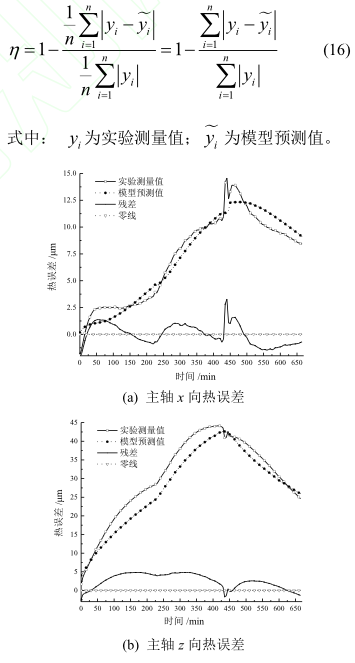
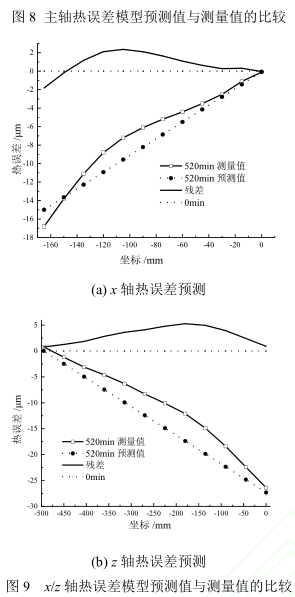
主轴x/z方向的热误差模型预测值的R和分别为 0.9μm、3.2μm 和 88.4%、90.7%;x/z 轴热误差模型预测值的 R 和 分别为 1.4μm、3.4μm 和82.9%、71.3%。证明热误差模型具有很高的准确性,在工程实际中还需进一步验证。预测模型之所以没有达到百分之百,任何一种模型都存在自身的模型误差。此外,机床的误差包括伺服误差、插补误差、跟随误差、几何误差、安装误差等,建模过程中这些系统误差未予考虑,都会导致预测模型精度的降低,因此预测模型都存在一定的误差。
3.3 机床热误差补偿工程应用
热误差补偿系统的总体结构设计主要有温度采集系统和 PLC 补偿系统两部分组成。温度采集系统用于获取热敏感点的温度值,并对采集的温度信号进行滤波、放大及 A/D 转换。获取温度之后在PLC内部根据前面的数学模型分别计算出每个轴的补偿参数tanoK。PLC 将补偿参数通过Siemens828D 数控系统内部特有的 PLC 与 NC 数据通信接口数据块 DB1200 写入 NC 系统内部,NC 系统会根据热误差补偿参数对机床各轴的插补指令做相应调整,从而提高了机床各轴的定位精度。
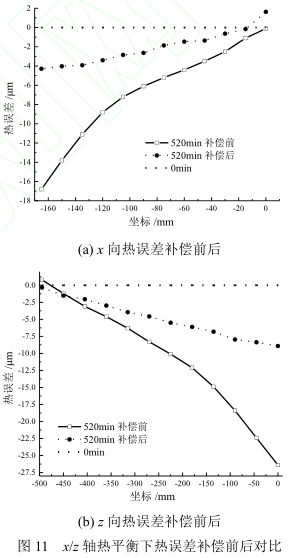
冷态下测量结束后根据实验测量原理开始运转机床,直至机床达到热平衡状态。机床在热平衡状态下补偿前和补偿后的热误差如图 11 所示。实验过程中主轴与进给轴同时运转,使得机床主轴与进给轴的热误差耦合在一起,从而验证热误差耦合模型的准确性。补偿前 x/z 轴的定位精度为18.6μm、24.3μm;补偿后 x/z 轴的定位精度为7.4μm、10.5μm,补偿后 x/z 轴的定位精度提高了60.3%、56.6%,充分验证了热误差耦合模型的准确性。
4 结 论
本文深入研究了机床热误差补偿理论及西门子 828D 数控系统热误差补偿机制,开发了基于828D 的热误差补偿系统, 运用多元线性回归与模糊聚类相结合的方法建立机床各轴的热误差数学模型,并分析了主轴与进给轴之间热误差耦合与解耦过程,建立了主轴与进给轴之间的耦合模型,利用模糊聚类方法对温度测点进行优化,选取热敏感点典型温度变量,降低了温度变量之间多重共线性的问题,提高了热误差模型的预测精度。最后,将建好的主轴与进给轴耦合模型嵌入 PLC中,在浙江海德曼机床厂生产的 HTC550/500 系列车床上得到实际应用,并且进行批量生产,机床在不同温度下的定位精度得到明显的提高,也为后期机床热误差的研究工作提供了重要依据。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息




