关节轴承冷挤压装配的有限元仿真分析
2014-9-28 来源:数控机床市场网 作者:福州大学机械工程及自动化学院吴连平杨晓翔
摘要:针对关节轴承挤压装配后内外圈可能会出现间隙过大、过小或者不均匀等现象,以有限元软件 ABAQUS为平台,根据 GEW12DEM1T 关节轴承冷挤压装配的实际情况,建立二维轴对称弹塑性有限元模型。研究关节轴承挤压变形过程和回弹过程,得出挤压过程中金属塑性成形的流动规律、内外圈接触应力分布情况和回弹后内外圈间隙分布情况。挤压后内外圈接触应力分布情况表现为中间小两端大;而回弹后,内外圈间隙分布情况也表现为中间小两端大。
关键词:关节轴承;冷挤压;装配;有限元法
关节轴承广泛应用于航空、航天、风电、动车、重载铁路货车等高技术行业。冷挤压作为关节轴承一种重要的装配方法,具有高效、优质、低耗等优点。目前对于冷挤压模具及轴承成形工艺的设计大多基于经验,费时、费力且效率低。
轴承冷挤压装配过程的数值模拟对提高产品的生产效率和产品质量具有重要意义,已有部分学者用有限元方法对轴承挤压过程进行了研究。
文献[1]分析轴承双收口成形相对单边收口成形的优势;文献[2]分别采用二维轴对称模型和三维模型对轴承挤压成形进行模拟,得出二者模拟结果差别小于1%的结论。
装配过程中,轴承内外圈之间不同接触应力将导致其间的衬垫被不均匀挤压,而接触应力较大处可能导致衬垫局部损坏;回弹后,内外圈间隙可能出现的不均匀现象对轴承也会有较大的影响。文中选用 GEW12DEM1T 轴承,采用实际生产中所使用的模具和定位套,对轴承的冷挤压装配过程进行数值模拟。观察轴承挤压变形过程和回弹过程,并对挤压过程中金属塑性成形的流动规律、内外圈接触应力分布和回弹后内外圈间隙分布进行分析。
1 基本假设及原理
1.1 建模假设
关节轴承挤压装配过程是一个复杂的大弹塑性变形过程,该过程涉及材料非线性、几何非线性、接触非线性等问题。假设材料性能和弹塑性变形过程符合 Mises 屈服准则并满足Coulomb 摩擦定律。在弹性阶段,应力应变关系符合Hooke定律,进入塑性状态后符合Prandtl-Reuss 假设。应满足的基本方程3 有: (1)弹性阶段,σ = Deε,其中 De为弹性矩阵;(2)弹塑性阶段,dσ = Depdε,其中 Dep为弹塑性矩阵。
1.2 轴承挤压原理
轴承挤压原理如图1 所示。由图 1a 可知,轴承夹在上下模之间。在挤压过程中,下模不动,上模和上定位套受到压力之后以一定速度向下运动,而下定位套受到轴承内圈施加的作用力也向下运动。由于定位套受到压簧的反向作用力,故模具与定位套之间存在一定的相对速度。图 1b为挤压后上下模和定位套的相对位置。在挤压装配过程中,塑性变形和摩擦会消耗机械能。其塑性变形的载荷来自3个方面:外圈与模具接触点的弯曲载荷;径向方向的压缩力;整个成形过程中,外圈与模具之间的摩擦力。
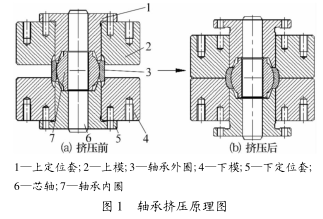
2 挤压过程的建模
2.1材料与建模
选用 GEW12DEM1T 关节轴承进行模拟。内圈材料为 9Cr18Mo,密度为7700 kg/m3,弹性模量和泊松比分别为2.1×105MPa和0.3。外圈材料为 0Cr17Ni4Cu4Nb,密度为7780 kg/m3, 弹性模量和泊松比分别为2.1×105MPa 和0.27。外圈的弹塑性行为可通过拉伸试验获得名义应力与名义应变的关系曲线,然后通过(1)~(3)式获得真实应力与塑性应变的关系[4]。内圈与外圈之间的自润滑复合衬垫材料为酚醛树脂和聚四氟乙烯浸渍玻璃纤维,由于衬垫材料各向异性且对挤压过程影响很小,故可忽略其对成形过程的影响。
σ = σnom(1 + εnom),(1)
ε = ln(1 + εnom), (2)
εp= ε - σ/E, (3)
式中:σ为真实应力; σnom为名义应力; ε为真实应变; εnom为名义应变; εp为塑性应变; E 为弹性模量。
根据实际装配条件,对模具和轴承进行建模。由于挤压过程中轴承几何形状和受力都是对称的,故建立二维轴对称模型。芯轴、模具及定位套均采用解析刚体进行求解。每个刚体设置一个参考点,用参考点代表其运动。根据模具和轴承实际尺寸完成每个零件的几何模型,并按照实际工况进行装配,如图 2 所示。
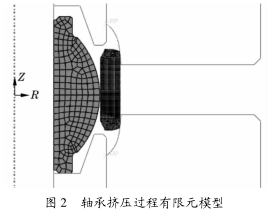
2.2 接触定义
根据运动关系, 定义 8 个接触对。接触面之间的摩擦采用 Coulomb 摩擦定律。
即 τf= μτn, (4)
式中: τf为摩擦力; τn为法向接触应力;μ 为摩擦因数。根据文献[5]选取摩擦因数为 0.11。
2.3载荷与约束定义
根据实际挤压情况,对芯轴和下模施加3个方向的约束,上模和定位套有 Z 轴方向的进给运动,约束 R 方向的移动和绕 Z 的转动。为缩短运算时间,在保证准静态的前提下,将成形速度范围定为 15 ~60 mm/s[4 。分3个分析步:(1)设定位套速度为20 mm/s,上模速度为30 mm/s;(2)设定位套速度为 25 mm/s,上模速度为 41.937 mm/s;(3) 设定位套速度为 20 mm/s,上模速度为 40mm/s。其中,上模速度根据分析步时间和定位套速度求得。
2.4 网格划分
由于挤压过程中外圈塑性变形较大,为消除过大应变产生的网格畸变,外圈采用 ALE 自适应网格划分技术。选取 4 节点双线性轴对称等参数单元,单元总数为 3 747,节点数为 3 894。由于内圈只产生弹性变形,且不是重点分析对象,故对其粗略划分网格。选取 4 节点双线性轴对称等参数单元,单元总数为 172,节点数为 204。
2.5 回弹模拟
回弹过程的模拟采用 ABAQUS/Standard 静态隐式分析,将成形过程中的模具和定位套去除,并对内圈和外圈施加 Z 方向的约束,回弹分析模型如图 3 所示。
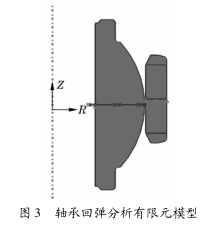
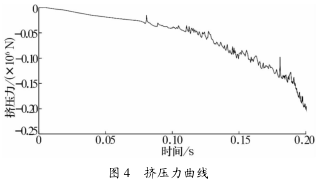
3 计算得出挤压过程中挤压力的变化曲线如图4 所示
由于加载过程中变形不均匀,开始增量步中,外圈大部分尚处于弹性变形阶段,故曲线下降缓慢。又因为此时挤压力较小,摩擦力对金属流动影响较小,曲线波动较小。随着模具的下压,材料逐渐进入受压状态,越来越多的材料发生塑性变形,挤压力快速增加,外圈受到的压力也增大,使得外圈接触表面摩擦力对金属质点流动不均匀性的影响也变大,导致挤压力的波动越来越明显,其最大挤压力为 255 349 N。
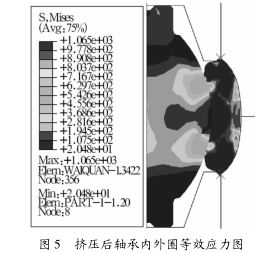
3. 1 挤压后轴承内外圈的 von Mises 等效应力分布图如图所示。
由图可知,外圈与模具接触处存在明显的应力集中现象,局部应力较大,最大值达到 1065 MPa。沿外圈径向方向,沿模具与外圈的接触面到外圈中部,由于外摩擦的影响逐渐减弱,应力值相对降低。又因外圈的弯曲变形,外圈内侧受到较大的压应力,故沿径向方向应力值先降低再上升。
3. 2 挤压后外圈的等效塑性应变如图 6 所示
由图可知在挤压过程中金属的流动情况。外圈两端存在明显的死区和剧烈变形区,外圈上端最大等效塑性应变为 3.297。主要是因为在挤压过程中,受定位套和模具形状及摩擦力的影响,金属沿阻力较小方向流动,从而使两端变形加剧。

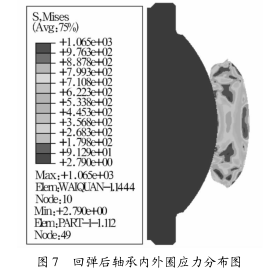
卸载后的回弹主要表现为外圈曲率半径增大。回弹后内外圈 von Mises 应力分布图如图 7所示,外圈外侧边缘有较大的残余应力,最大值达到1065 MPa。主要原因有2个:一是模具型腔模角过大及接触面之间的摩擦导致应力分布不均;二是外圈弯曲时,外侧边受拉伸长,内侧边受压缩短,外力撤除后,外侧存在压应力,内侧存在拉应力。
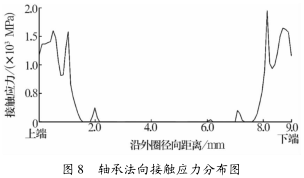
挤压完成后,从上端到下端,内外圈之间的法向接触应力分布如图 8 所示。由图可知,不同接触位置的接触应力不同。受模具挤压的影响,离外圈端面0.5 mm 处受到的接触应力较大。由于金属塑性流动不均匀,上下两端变形并不完全对称。最大接触应力为 2 331.66 MPa。
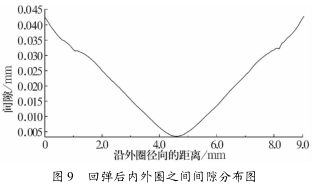
挤压装配过程中,外圈产生的总变形由塑性变形和弹性变形组成。撤除模具和定位套后,塑性变形留存下来,而弹性变形完全消失。此过程中轴承外圈外侧因弹性恢复而缩短,内侧则伸长。由于轴承两端产生的弹性变形相对中部较多,故回弹量也较大。回弹后内外圈之间间隙分布如图9 所示。由图可知,两端间隙较大,最大间隙出现在轴承下端面(0.0527 mm),最小间隙出现在轴承中部(0.0054 mm),最大间隙与最小间隙相差0.047 3 mm。
从间隙差来看,用该模具挤压后的轴承是合格产品,符合实际生产要求。而从轴承内外圈应力分布和法向接触应力分布情况可知,该挤压产品却不是最优产品,还可通过优化模具形状,以减小接触面之间的接触应力和摩擦力对塑性成形的影响。
4 结论
(1) 以有限元软件 ABAQUS 为平台,根据轴承冷挤压的实际工作情况,建立了 GEW12DEM1T轴承二维轴对称弹塑性有限元模型,得出的应力、应变分布符合实际情况。
(2) 通过数值模拟研究了挤压过程中轴承内外圈之间法向接触应力的分布和回弹后内外圈间隙分布情况,得出轴承端部的法向接触应力和内外圈之间的间隙比轴承中部的大。
参考文献:
[ 1]Yang Yulin,Huang Shijun.Study on New FormingProcess for Spherical Plain Bearing and Optimum of theNecking Force[C].International Conference on Infor-mation Engineering,2010,229:216 -219.
[ 2]Alex Orsolini,Julian D Booker.Modelling CapabilitiesRequired for the Double Nosing Process in the Assem-bly of Spherical Plain Bearings J]. Journal of Engi-neering Manufacture,2012,226(5):930 -940.
[ 3]谢水生,李雷.金属塑性成形的有限元模拟技术及应用 M].北京:科学出版社,2008.
[ 4]庄茁.基于 ABAQUS 的有限元分析和应用[M].北京:清华大学出版社,2004.
[ 5]Reid S R,Harrigan J J.Transient Effects in the Quasis-tatic and Dynamic Internal Inversion and Nosing of Met-al Tubes J].Internation Journal of Mechanical Sci-ence,1998;40(2-3):263 -280.
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息




