数控插床无冲击让刀机构的凸轮轮廓线设计与计算
2018-7-18 来源: 天津机电职业技术学院 作者: 李 欣 张静双 徐 慧
摘要: 为了提高数控插床冲程频率和运动稳定性,减小由于让刀运动带来的冲击; 针对目前数控插床让刀运动冲击引起的振动较大且影响插削加工精度、限制冲程次数的问题,提出了通过凸轮曲线优化设计达到无冲击让刀运动的设计方法。首先设计双共轭凸轮机构并对双共轭凸轮的主动曲线进行数学建模,求取双凸轮曲线,达到设计目的。
关键词: 数控插床; 让刀机构; 双共轭凸轮; 等距曲线; 无冲击
机床振动是影响机床加工精度和机床稳定性的关键因素,考虑机床大型零件的动静刚度、机床往复运动与回转运动的频率,进而确定机床的动、静刚度指标,是机床设计的关键环节。
数控插床的主轴往复运动和让刀运动是其规则振动的主要驱动源,改善让刀运动的运动状态和减小由于让刀运动带来的冲击,是让刀机构设计的一个关键。目前为了适应更复杂的机床应用环境,通过优化凸轮曲线,设计不具有刚性冲击甚至不具有柔性冲击的双共轭凸轮让刀机构迫在眉睫。数控插床由液压缸对刀轴进行驱动提供往复插削运动,可以进行正常的等速上下往复运动。由于液压缸活塞杆的影响使得油缸上下油腔面积不等,可以利用这一特性,改变刀轴下行切削运动和上行空程运动的时间比例,根据油腔截面积比例将其时间比例改变为 1∶2,即满足慢速切削快速空程返回,工作效率得到很大提高。则让刀电动机需要频繁地加减速,不利于数控系统的稳定。通过分析共轭双凸轮让刀机构的运行特性,通过设计凸轮曲线就可以解决上述问题。本文以数控插床满足等速往复运动的让刀机构为例,对其双共轭凸轮轮廓线进行设计; 满足下行与上行时间比 2∶1 的让刀机构双共轭凸轮轮廓线原理与其类似,不再赘述。
1、让刀机构功能需求
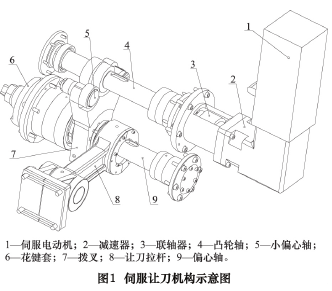
图 1 是伺服让刀机构示意图。
伺服电动机驱动的数控插床让刀机构采用如下技术方案: 伺服电动机可以根据主轴运动的位置进行数控调速,以满足于让刀机构与插削机构的运动周期同步。伺服电动机通过减速器和联轴器将运动传递到凸轮轴上,共轭双凸轮在任意时刻与拨叉上的两个滚子均保持接触,共轭双凸轮曲线与各自所对应的滚子的接触点啮合,其凸轮形状曲线满足让刀机构运动曲线特征,使拨叉进行往复摆动,拨叉带动偏心轴往复摆动,偏心轴推动让刀拉杆使得让刀拉杆前端做往复移动,从而推动数控插床刀架形成让刀运动。拨叉上的其中一个滚子的轴是小偏心轴,可以通过它的旋转控制两滚子与共轭凸轮的配合以弥补机加工的误差。伺服电动机驱动的数控插床让刀机构由于采用本技术方案,因而解决了让刀机构和插削机构运动周期无法同步的问题。具体实施方式: 伺服电动机 1 带动减速器 2,通过联轴器 3 带动凸轮轴 4 转动,凸轮轴 4 推动滚子,使拨叉 7 摆动,拨叉 7 通过键带动偏心轴 9 摆动,偏心轴 9带动让刀拉杆 8 往复运动。伺服让刀机构的机械零件均可设计,其中设计难度最大的是凸轮轴的双共轭凸轮轮廓线部分。
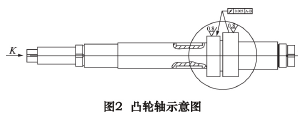
图 2 是凸轮轴的示意图,圆圈中的部分即为其双凸轮部分.
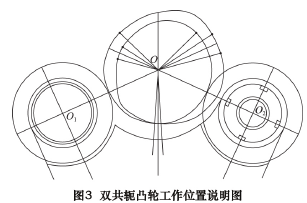
图 3 是其双共轭凸轮部分工作位置说明图。
让刀机构需要满足的让刀运动的运动关系如图 4 所示。
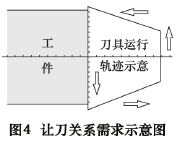
左侧阴影部分是被加工工件,右侧封闭曲线是刀具运行轨迹的原理图。刀具在一个往复冲程中需要向工件的反方向运动一次。如何设计刀具的运动轨迹,亦即如何设计让刀凸轮轮廓线,是本文的主要内容。要通过轮廓线的设计与计算,使得让刀运动规律振动最小化,避免刚性冲击和柔性冲击。所谓无冲击,即所受力连续、不突变且平滑过渡,数学表达为: 运动曲线的一阶导数连续且可导、运动曲线的二阶导数连续。
2 、共轭双凸轮轮廓线设计
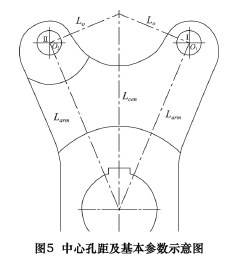
2. 1 中心孔距及基本参数的确定选择
“5-12-13”勾股序列作为本文的参照,该序列可以很方便地上下扩展。根据类比法和让刀力量的需求计算,选择“5-12-13”勾股序列的 18 倍作为本文的设计参数。

上述参数的空间位置关系,如图 5 所示。
2. 2 让刀量及凸轮升程的确定
根据机床设计要求,数控插床的让刀量需求为不小于 0. 80 mm。根据供应商 INA 公司轴承的型号规格,将滚子的半径 R 确定为:

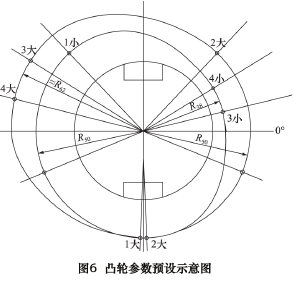
凸轮参数预设结果如图 6 所示。

0. 889 4 mm>0. 80×1. 1 mm 上述参数满足要求。
2. 3 圆弧转角的确定
根据插床设计经验,工件厚度/冲程长度>93%。计算得圆弧转角: 2×arcsin[0. 93]= 137°为了计算的简便和工作的可靠性,将圆弧转角取值 138°。
2. 4 升降函数的确定
由机械原理凸轮传动知识可知,“等加速等减速”和“余弦加速度”等运动规律存在柔性冲击,而“3-4-5 多项式”运动规律,不存在柔性冲击,适用于“高速中负荷”的场合。本文凸轮过渡曲线采用“3-4-5 多项式”,为了避免冲击,该多项式要满足以下条件:
(1) 首尾与圆弧曲线相接。
(2) 一阶导数连续,并且首尾点的一阶导数为 0。
(3) 二阶导数连续,并且首尾点的二阶导数为 0。
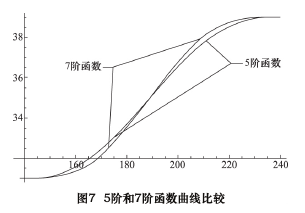
至于是否有必要将升降函数曲线的最高阶次升至7 次函数,并且要求“三阶导数连续、首尾点的三阶导数为 0”呢? 其比较结果,如图 7 所示,7 阶函数的冲击反应会更小,但其首尾段的直线延伸更明显,不利于让刀机构的快速让刀运动。所以选择 5 次函数,是正确可取的。

数,其他表示方法类同。
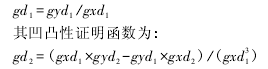
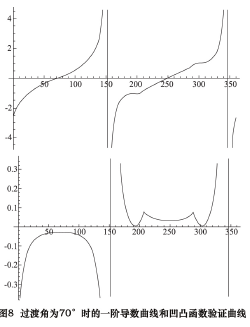
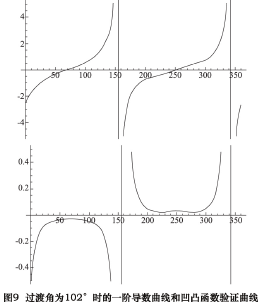
经过反复验算,本凸轮轮廓线的最小过渡角度为70°。当过渡曲线的过渡角为 70° 时,其一阶导数曲线和凹凸函数验证曲线如图 8 所示。由图 8 可见,该曲线在过渡部分,二阶导数大于 0,该曲线为凸曲线。亦即: 只要大于 70°的过渡曲线都满足凸曲线的特性。经过反复计算,当过渡角为 102°时的曲线其一阶导数曲线和凹凸函数验证曲线最平滑,在满足无冲击的前提下,还能做到运动关系相对最平稳。
当过渡曲线的过渡角为 102°时,其一阶导数曲线和凹凸函数验证曲线如图 9 所示。
2. 6 升降函数的参数计算
按照 2. 4 节设定的 5 次函数曲线方程和需要满足的条件,求解下列方程组,
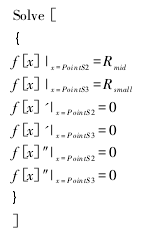

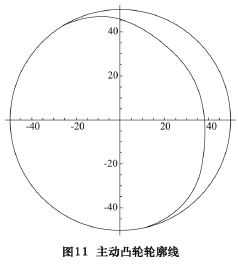
2. 8 求解主动凸轮轮廓线的等距曲线
根据下列公式组合,
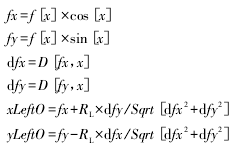
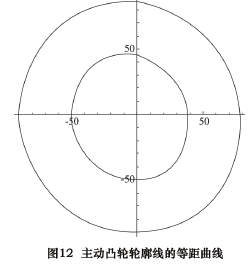
求取主动凸轮轮廓线的等距曲线,亦即与主动凸轮啮合的滚子的中心与主动凸轮相比较的轨迹曲线。其等距曲线计算结果,如图 12 所示。图中,内侧曲线为主动凸轮轮廓线,外侧曲线为其等距曲线。
2. 9 求解被动凸轮曲线
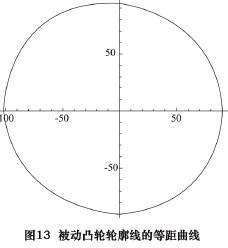
根据图 5 所示的中心矩及拨叉基本参数,利用2. 8 节求解得的主动凸轮轮廓线的等距曲线,求解被动凸轮轮廓线的等距曲线,如图 13 所示。
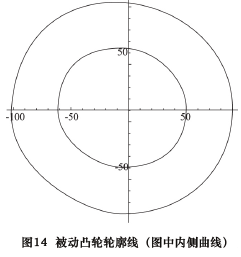
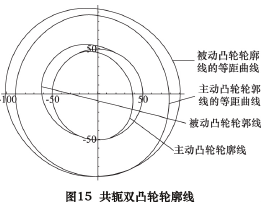
同样利用 2. 7 节所列公式,改变其法线方向,即可以求取被动凸轮轮廓线,如图 14 所示。2. 10 数据输出至此,已经求取共轭双凸轮的两条轮廓线,其位置关系和曲线表示如图 15 所示。将上述主动凸轮轮廓线和被动凸轮轮廓线的曲线以等距离点的方式输出为数控凸轮磨床可以识别的数控程序,即可完成对凸轮轴的凸轮轮廓线磨削加工。
经过求解其过渡点的角度坐标,将其详细轮廓线描述如下( 如图 16 所示) 。
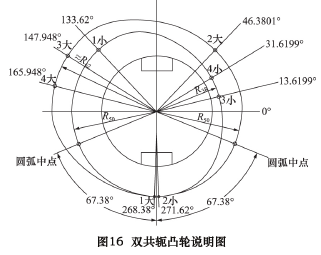
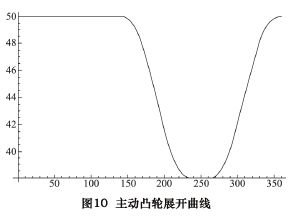
图 16 中由“1 小—2 小—3小—4 小—1 小”所连接的封闭曲线为其中的小凸轮的曲线,小凸轮即为主动凸轮,其曲线的变化决定了让刀运动的变化规律。其中,“1 小—2 小”区间为 R = 50 mm 的圆弧,“3小—4 小”区间为 R = 38 mm 的圆弧,“2 小—3 小”和“4 小—1 小”区间为对称的降程曲线和升程曲线。图 16 中由“1 大—2 大—3 大—4 大—1 大”所连接的封闭曲线为其中的大凸轮的曲线,大凸轮即为被动凸轮,其曲线的变化决定了是否可以使得两个凸轮曲线与其对应的两个滚子在任意时刻接触。其中,“1 大—2 大”区间为 R=50 mm 的圆弧,“3 大-4 大”区间为的圆弧,其半径由计算得约等于 62 mm,“2 大—3 大”和“4 大—1大”区间为计算所得的对称的降程曲线和升程曲线。
2. 11 验证让刀量和运动关系
根据上述计算结果,求解验算让刀量与旋转角度的关系( 如图 17 所示) 和让刀量与插削位置的关系( 如图 18 所示) ,并以图 19 局部表达了其过渡区间的运动曲线。
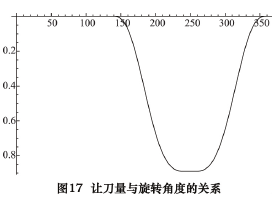
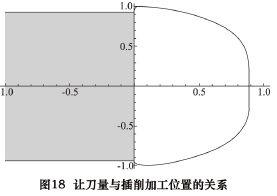
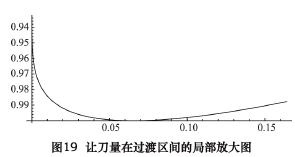
由图 17~19 可知,让刀量和让刀运动关系平滑过渡,满足题设的条件。
3 、共轭双凸轮设计结果及实际应用
利用上述计算结果加工的双共轭凸轮应用现场照片如图 20 所示。实际应用表明,本文所述双共轭凸轮无冲击,上下扩展适应性强,可在插床中广泛应用.

投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息




