凸轮磨床 X － C 廓形误差推导与仿真-数控机床市场网

您现在的位置：磨床网> 技术前沿> 凸轮磨床 X － C 廓形误差推导与仿真

凸轮磨床 X － C 廓形误差推导与仿真

2018-4-12 来源：北京第二机床厂有限公司北京信息科技大学作者：张培硕李伟华韩秋实李启光等

摘要: 在数控联动加工时，由数控系统引入的跟踪误差是影响凸轮加工廓形误差的主因之一，通过研究凸轮磨床跟踪误差，分别推导 X 轴、C 轴跟踪误差与廓形误差计算模型，进一步推导出 X － C 轴联动时跟踪误差与廓形误差的计算模型。借助 MATLAB 工具编写程序，分别实现数学模型仿真和模拟加工仿真，将实验采集的跟踪误差采用不同的方法引入到仿真中，通过仿真结果对比，验证了X － C 廓形误差数学模型的正确性。

关键词: 数控凸轮轴磨床; 跟踪误差; 廓形误差; 仿真

在数控凸轮轴磨床加工过程中，X 轴和 C 轴要求随加工形状的不同瞬时启停或改变速度，控制系统要实时精确地控制坐标轴运动的位置与速度，由于系统的稳态和动态特性影响了各坐标轴的协调运动和位置精度，从而产生了凸轮的廓形误差。

数控凸轮轴磨床的伺服系统是影响磨削质量最关键的部分之一。作为执行部件的伺服驱动系统和电动机，能否准确执行给定的命令，对最终的磨削质量的影响是显而易见的。凸轮轴磨床多采用砂轮架住复运动和工件旋转运动的联动来实现凸轮的磨削加工，在数控联动加工时，伺服系统引入的跟踪误差是产生廓形误差的一个重要因素。国内学者近几年涉足了数控系统的跟随误差研究领域，其中，浙江大学朱年军等推导了数控加工中稳态误差的形成过程，并从直线和圆弧轮廓误差模型出发探讨了数控跟踪误差和轮廓误差之间的关系

; 兰州理工大学孙建仁等从分析轮廓误差、跟随误差和位置环增益着手，分析两种基本插补运动的轮廓误差及其相应的跟随误差与轮廓误差之间的关系; 南京航空航天大学滕福林等针对不同类型的位置给定，仿真分析了动态位置跟踪误差的产生机理，并提出采用 S 曲线给定可以大大减小实际系统的动态位置跟踪误差的方法。

以上 3种方法研究的对象都是通用的数控系统的简单插补过程，未涉及到复杂联动加工，如果将以上研究成果直接应用到加工凸轮的 X － C 联动是不科学的。此外，华科技大学李勇等从系统传递函数入手，完成了数控凸轮轴磨床控制系统的建模，引入粒子群算法，优化了 PID参数，此方法没有涉及到跟踪误差数学模型的推导问题。

本文主要完成工作是，在数控凸轮轴磨床的 X －C 轴联动系统中，推导跟踪误差引起的廓形误差数学模型，利用加工实验采集到的跟踪误差值，借助 MATLAB工具实现仿真，来验证数学模型。

1、 X － C 轴跟踪误差引起的廓形误差数学模型推导

廓形误差是指任意位置处实际廓形轨迹与理论廓形轨迹之间的最短距离。在磨削过程中，凸轮轴磨床通过两轴联动合成运动轨迹，完成凸轮廓形加工，由于各个轴都存在跟踪误差，运动分别会稍有偏差，因此，最终体现在磨削工件上的跟踪误差是二者合成的结果。

1． 1 X 轴跟踪误差引起的廓形误差数学模型推导

对于凸轮轴磨床而言，X 轴跟踪误差，是指砂轮在伺服系统要求到达指定位置时，实际位置偏离所要求的理论位置的误差值。设 X 轴跟踪误差为 Δx，如图 1所示，凸轮轮廓偏差量为 εx。

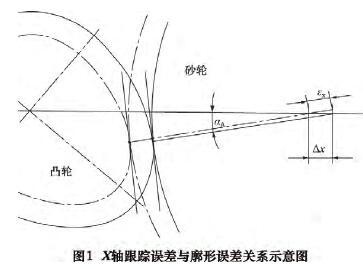
由几何关系，可以得出:

式( 2) 即为 X 轴的跟踪误差与廓形误差的数学模型。

1． 2 C 轴跟踪误差引起的廓形误差数学模型推导

凸轮磨床 C 轴的跟踪误差，是由于加工凸轮时实际磨削点在 C 轴上偏离了理论磨削点而引起的凸轮廓形的加工误差。根据凸轮轮廓解析法，见图 2，s0为基圆半径，s 为升程值，δ 为转角值，e 为偏心距，rr为滚子半径。有:

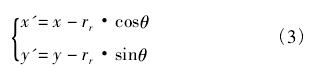
式( 3) 即为凸轮工作过程中廓形的直角坐标。

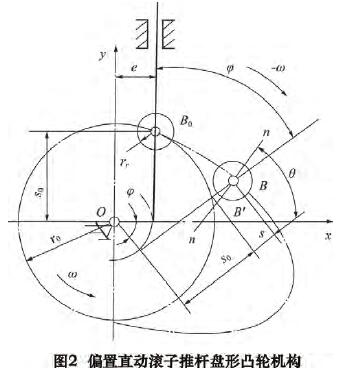
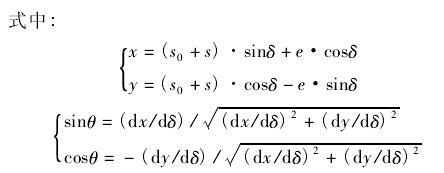
将滚子视为砂轮，该式就转化为磨削模型，借助 X坐标计算廓形误差，设极角误差为 Δδ，容易得出:

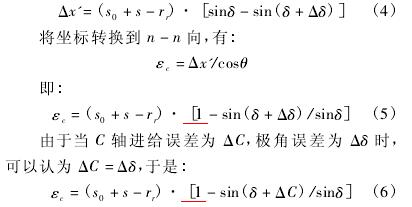
式( 6) 即为 C 轴跟踪误差与廓形误差的数学模型。

1． 3 X － C 跟踪误差引起的廓形误差数学模型在凸轮实际磨削时，C 轴跟踪误差与 X 轴跟踪误差是同时存在的，由于在式( 2) 与式( 6) 建立起的数学模型中，计算出的廓形误差都是法向值，因此，综合考虑 C 轴跟 X 轴，由它们造成的凸轮廓形误差 ε 为:

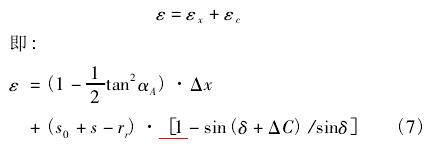
2 、实验验证

2． 1 实验凸轮轴磨床数控系统简介

数控凸轮轴磨床通常采用 X － C 两坐标联动实现凸轮轮廓的磨削，以 PMAC 卡为主要运动控制核心，控制 X 轴砂轮架前后往复移动和 C 轴工件主轴旋转运动，Z 轴工作台的左右移动实现凸轮轴的自动磨削加工循环和砂轮的自动修整，C 轴由电主轴驱动，X 轴采用直线电动机驱动，Z 轴由交流伺服电动机驱动。

磨削过程中，X 轴执行磨削进给和退避到安全位置，Z轴移动依次磨削凸轮轴上的各个凸轮。凸轮轴磨床数控工作原理图如图 3 所示。

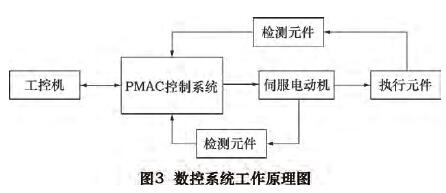
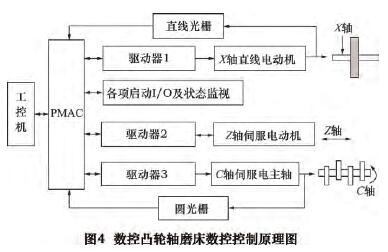
数控凸轮轴磨床数控控制原理图如图 4 所示，X轴直线电动机带动砂轮架水平往复移动，C 轴伺服电主轴带动工件主轴转动，X － C 两轴联动，实现凸轮廓形加工，Z 轴伺服电动机带动工作台移动，完成整根凸轮轴的加工。

2． 2 跟踪误差采集

本文采用双端口 RAM 数据读取方式，利用双端口所带的函数进行数据采集，这种方式更加的方便，双端口 RAM 函数封装了 PMAC 数据读取过程，用户调用相应的函数即可从双端口 RAM 中直接读取运动参数，不需设置采集源及数据地址，双端口 RAM 有很多运动参数采集函数，利用这些函数就能采集电动机的状态、实时位置、速度、跟随误差等等。

采集的实现是通过编写采集软件来完成，为提高采集时间精度，软件采用多媒体定时器，设置多媒体定时器采集间隔 20ms，定时器精度 1 ms，采集结果写入数据文件。实验共采集 3 组数据，按 C 轴转速分别为 30 r/min、60 r / min、90 r / min，从低到高依次为数据 1、数据 2、数据 3。

2． 3 仿真验证

2． 3． 1 仿真实现方法

( 1) 计算模型仿真

在伺服跟踪误差与凸轮廓形误差数学模型建立的基础上，借助 MATLAB 工具，编写出仿真程序代码，将凸轮升程拟合成凸轮廓形，伺服跟踪误差值由式 7 的数学模型引入，在法相将叠加到凸轮廓形上，可得到由单一曲线构成的凸轮实际廓形。该仿真方法部分MATLAB 程序如下:

( 2) 模拟加工仿真

非圆曲面零件采用 X － C 联动磨削时，实质是一种砂轮包络，为了便于观察与计算，常采用砂轮反转法即工件不动、砂轮反向旋转对非圆曲面零件加工过程进行分析。借助 MATLAB 工具，编写出反转法模拟凸轮廓形加工的仿真程序，跟踪误差分别由 X 轴跟踪误差 Δx 和 C 轴跟踪误差 ΔC 分别引入，程序运行时，砂轮反方向旋转一周，可得到由多重砂轮轮廓逼近出的凸轮实际廓形。

该仿真方法部分 MATLAB 程序如下:

2． 3． 2 仿真结果对比分析

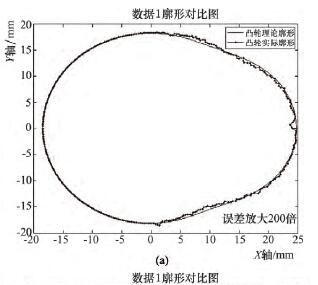
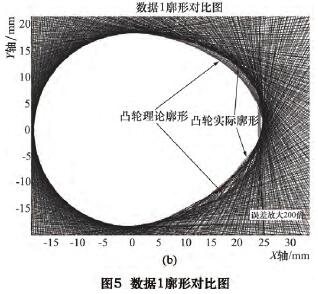
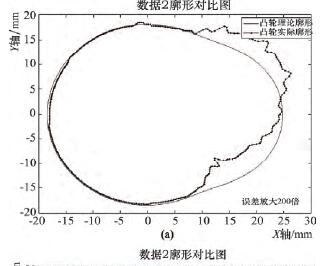
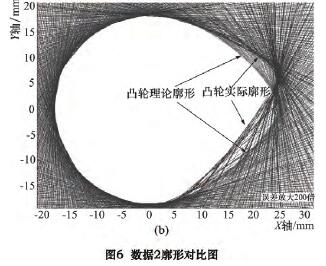
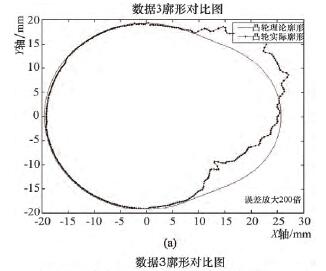
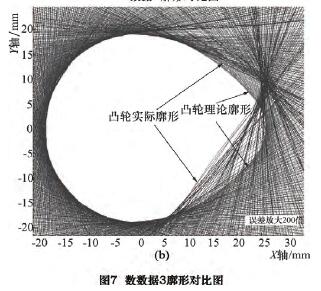
将采集到的 X 轴、C 轴跟踪误差的 3 组数据分别导入 MATLAB 程序，仿真出凸轮理论廓形与实际廓为了让误差效果明显，误差被放大了 200 倍，如图5 ～ 7 所示。图 5a、6a、7a 三幅仿真图，由单一曲线构成，为本文推导出的数学模型仿真结果; 图 5b、6b、7b三幅仿真图，由多重曲线轮廓构成，为砂轮反转法模拟凸轮加工的仿真结果。将图 5 ～ 7 中上下两幅图，分别进行对比，可以得出廓形误差曲线整体变化趋势基本一致，桃尖整体位置沿 Y 轴正方向偏移，随着 C 轴速度的依次增加，偏移量依次增加。

分析不同仿真方法的廓形对比图，可发现较之于理论廓形，凸轮实际廓形曲线明显向上偏移，二者仿真结果基本一致，但是计算模型仿真出的实际廓形与反转法模拟加工仿真相比，误差有轻微波动，分析原因，在实际加工过程中，除去伺服跟踪误差以外还有其他误差因素影响，有一定程度的波动是合理的。这就证明了推算的伺服跟踪误差与廓形误差的数学模型式( 7) 是正确的。