T_S模糊模型变结构的机器臂轨迹跟踪控制①
2016-8-2 来源：江南大学，轻工过程先进控制教育部重点实验 作者：王宪 盛巍 宋书林 平雪良
摘要：针对不确定性的机械臂轨迹跟踪问题，结合滑模变结构和T．S模糊模型的优点，给出一种基于T．S模糊模型的变结构轨迹跟踪的方法。首先采用T．S模型建模，得到机械臂的模糊模型：然后设计出保证机械臂全局渐近稳定的滑模控制器。仿真结果表明，所设计的模糊变结构控制器与普通变结构控制器相比，可使机械臂无论在计算时间、误差上都具有更大的优势和更强的鲁棒性。
关键词：非线性系统：模糊控制；滑模控制：
1 、引言
机器人轨迹跟踪控制的主要目的是通过给定各关节的驱动力矩，使得机器人的位置、速度等状态变量跟踪给定的理想轨迹【13】。传统控制方法大都在被控对象数学模型确定、定量化的前提下，却难以对复杂的、非线性的不确定系统进行有效而又精确的控制。智能控制的出现为解决此类问题提供了新的思路。文献【l】提出了针对非线性系统的模糊自适应控制理论，为不确定性系统的控制提供一种可行的控制策略：文献【2．5，11．13】等都对文献【1】方案进一步改进，取得了多方面进展，但是这些方法都存在一定的问题，如：传统的滑模控制(SMC)瞄刮因其在滑动模态对系统干扰和摄动具有鲁棒性而得到重视，但高频抖动的问题，以及输出力矩和跟踪误差精度上也有待提高：文献[11】在文献【12】的基础上将滑模控制与饱和函数有机结合，但是在追踪时间和误差上都有待商榷。据此分析，为了避免传统非线性控制器设计方法中迭代计算中近似值以及计算负担增加的问题，提高伺服控制器对于追踪误差和输出力矩上的控制精度，同时针对所需求的精确性使用适当选取的T．S模糊模型来近似原始非线性模型时，产生一些额外的系统不确定性(unccnain哆)。本文提出一种结合T．S模糊模型与变结构控制的控制器设计方法，这种控制器容易实现且不需要去解J∞obi方程式或不等式，同时运用T．S模糊模型的优点(计算快速)来减轻计算上的负担；通过仿真并利用两轴机器臂的模拟来验证算法的正确性。
2、机器人动力学模型
2．1动力学模型分析
自由度机器人的动力学方程由下式给出：
式中q,q,q,∈Rn为位移、速度和加速度矢量，M(q)∈Rn×n为对称正定的惯性矩，C(q，q)∈Rn×n为离心和coriolis力矩矩阵，G(q)∈Rn为重力矢量，F(q)∈rn”为摩擦向量，^d为外部未知有界干，f为控制输入力矩矢量。其中F(q)和d^为可能的不确定项，F(q)是由各种参数误差、降阶处理，以及建模时动态特性所^带的模型误差：d^主要指不确定的外部干扰。
机器人动力学方程(2．1)具有如下性质：
性质l：M(q)是对称正定矩阵，满足：
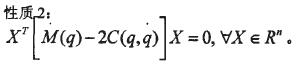
可知当系统的参数精确已知、且结构确定的情况下，控制律能保证闭环系统的全局稳定；但当系统存在结构参数误差、摩擦及干扰等不确定因素时，控制律就不能保证系统具有良好的动态性和稳定性；同时选择T-S模型来近似非线性模型、简化计算时，也会带不确定性因素。为了消除不确定性的影响。保证系统的渐近收敛，必须设计控制律来弥补T-S模糊模型来近似非线性模型所带来的不确定性。(其中这里的不确定性主要来自模型误差即)F(q)。
2．2问题描述
本文以一个二阶非线性系统为例，二阶非线性系统微分方程如下：
x1=x2
3、模糊变结构控制器的设计
3．1T-S模糊建模
T—S模糊模型是由一组“if-then明”模糊规则来描述非线性系统(2．2)的行为，每一个规则代表一个子系统，整个模糊系统即为各子系统的线性组合。第i条模糊规则对应的模糊状态方程为：
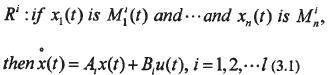
利用(3．2)式可将原始非线性系统改写成T-S模型：
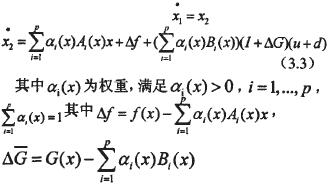
3．2控制器的设计
利用(3．3)式可改写以下型式：
3．3方法的敛散性
为了让系统状态在有限时间内到达顺?平面，我们提出以下假设；
也就是系统状态在有限时间内会到达顺滑平面。由以上的讨论我们会有以下的结果：
定理3．1：令假设3．1与假设3．2同时成立，则采用控制律(3．7)，(3．8)以及(3．12)时，此系统(2．2)会达到追踪的性能表现。
4、实验与仿真
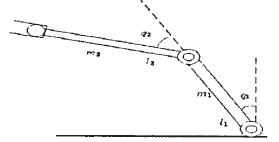
图4．1两轴机械手臂示意图
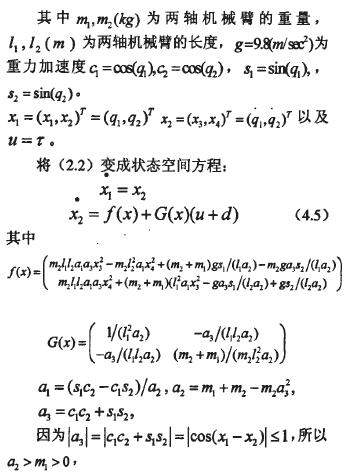
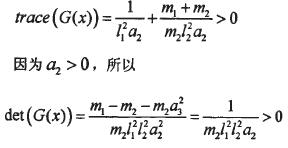
操作点的选定规则如下：
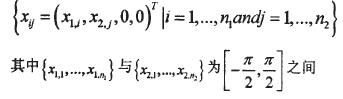
另一方面虽然T_s变结构控制律会比典型非线性变结构控制律需要较多的控制能量，可是在整个过程当中T．s变结构控制律所消耗的总能量有可能会比典型非线性变结构控制律来得少且过程中的总误差值也比较小。这可能是因为T-s变结构控制律一开始所需的能量较大，一开始能量较大会使得系统状态能快速地接近目标；而典型非线性变结构控制律一开始所需的能量较小，在过程中随着状态越来越靠近目标且越来越靠近顺滑平面其所需的能量也一直在变小，所以到达目标的时间会比较长。就总能量说，T-s变结构控制律一开始所需的能量较大，但是随着状态快速地到达目标而变小；反观典型非线性变结构控制律一开始所需的能量虽然比较小，但是接近目标的速度较慢，所以过程中典型非线性变结构控制律所消耗的总能量有可能会比较多。从控制律入能量图(图4．3)中可以观察到会有两个跳跃现象(Jump)，这是因为系统状态到达顺滑平面的缘故。同时这种情形也可以分别从图4．2观察到。在计算时间方面，我们将T-s变结构控制律与典型非线性变结构控制律各计算了106次之后发现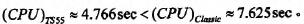
由此可以知道T-s变结构控制律可以节省计算时间。
由此可以知道T-s变结构控制律可以节省计算时间。 表4．1各项性能指标
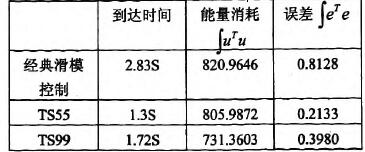
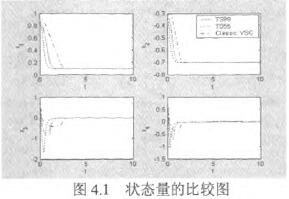
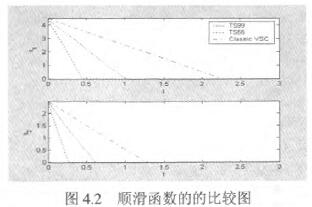
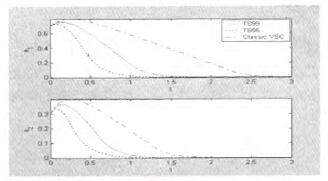
图4．4误差的比较图
5、小结
本文结合了T-s模糊模型与变结构控制理论并且应用在两轴机器手臂系统上。这种方法可以大量地减轻即时计算的负担，具有响应快速以及强健的特性。最后，增加模糊法则的数量可以降低控制输入的大小，也就是将系统操作区间划分多一点会使得控制输入变小以至于在实际应用上有控制输入大小限制时能够轻易地实现。同时，增加模糊法则地数量并不会造成额外的计算负担。由模拟的结果显示，这种结合T．S模糊模型与变结构控制的方法同样可以完成任务，而且在使用的能量、时间、追踪误差上比典型变结构控制方法来得少。
投稿箱：
如果您有机床行业、企业相关新闻稿件发表，或进行资讯合作，欢迎联系本网编辑部， 邮箱：skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表，或进行资讯合作，欢迎联系本网编辑部， 邮箱：skjcsc@vip.sina.com
