加工中心部件故障相关度评估
2018-5-18 来源: 机械科学与工程学院,长春工业大学 作者: 龙 哲,申桂香,张英芝,曾文彬,荣 峰
摘要: 为实现加工中心系统部件间故障相关度评估,采用相关故障机理分析与图论相结合建立系统部件故障传递有向图的方法,将系统部件相关度评估转化为复杂网络节点重要度计算,进而由邻接矩阵及其转置变换并结合 pagerank 算法,实现加工中心系统部件故障相关度求解. 计算结果表明: 故障相关度的大小与部件间故障关联关系成正比,存在故障相关的部件的故障相关度大于不存在故障相关的部件的故障相关度. 若部件被影响度大,影响度小,说明该部件是故障表象部件; 反之,响度大而被影响度小的是故障源部件. 提出的方法有助于故障诊断与维护.
关键词: 加工中心; 部件; 关联故障; 故障相关度; pagerank 算法
加工中心功能先进性及其结构复杂性,导致系统故障存在相关性,使系统多模、连锁故障频率有增加趋势. 早在 50 年代,在核反应堆设计和操作的初始阶段就发现了相关失效现象,1962 年 Lennox 等将其称为交叉揺合故障. 相关失效分析主要包括定性分析和定量计算. 定性分析常用方法是显示模型法,如事件树、故障树、因果表等; 定量计算主要指参数模型,如 B 因子模型、C 因子模型、基本参数( BP)模型、a 因子模型、多希腊字母( MGL) 模型等数,但这些定量模型多以共因失效为主. Pickles借助Domino 骨牌将独立的可靠性评价扩展成连续失效过程,借助指定的系数来刻画某一子系统故障对其相邻子系统的影响,但因假定的失效序列比较单一.
无法适用于故障的多路径传递方式; Sun 等构建了定量化分析关联故障的可靠性模型,并结合故障数据计算子系统的相关系数,但是该相关系数是一个综合指标. 很多学者借助 Copula 函数来研究故障相关性问题,文献用 Gumbel Copula 函数建立数控装备部件故障间函数关系,但无法体现相关关系的作用方向. 还有一些学者应用复杂系统相关理论对连锁关联故障进行研究,主要包含两个方面:
一是基于复杂网络理论的“小世界网络”模型、Watts 构造模型、Holme 等的相隔中心性模型、Motter 与 Lai 模型等进行连锁关联故障机理分析; 二是利用 Monte Carlo 模拟法、递归算法、基于 AHP 和灰色关联度选择故障序列等进行连锁关联故障路径搜索. 加工中心部件相关故障是连锁故障类型,且不存在冗余,因此,不能直接照搬电力系统连锁故障分析及相关度计算方法.
本文将相关故障机理分析与图论相结合,建立系统部件故障传递有向图,使系统部件相关度评估转化为复杂网络节点重要度计算,由邻接矩阵及其转置变换并结合 Pagerank 算法,实现加工中心系统
部件故障相关度求解.
1、系统关联故障建模与评估原理
工程实际中,系统部件的故障事件可能从系统中某一故障源开始,继而引发系列元件故障,这种关联故障的迅速传播最终导致系统崩溃. 本文引入图论构建系统部件故障传递有向图模型,将部件节点相关度转化为节点重要度. 应用邻接矩阵量化图中节点关联关系,邻接矩阵归一及转置变换形成系统状态转移矩阵,结合 pagerank 算法实现故障传递有向图中节点相关度计算.建模与评估流程如图
1 所示.

图 1 关联故障建模与评估流程
1.1 系统部件关联故障建模
故障传递有向图是将系统中各元件或子系统简化为图中的节点,单元间的故障传递关系则被简化为节点之间的有向边,依据系统各个元件或单元之间的故障相关关系,构建整个系统的故障有向传递模型
. 如果单元 i 出现故障会引发单元 j 出现故障,则存在从节点 i 到节点 j 的一条有向边.

1.2 基于 pagerank 算法的部件相关度评估
pagerank 算法原理: 若部件 M 故障导致部件 N故障,则可认为部件 M 传递给部件 N 一个重要度 p值,此值的大小取决于部件 M 的重要度 p( M) 以及出链数. 设任何部件的重要度都被平均传递到它所链接的部件. 由于部件故障之间存在相互链接关系,这个过程会一直迭代下去,最后部件重要度根据故障部件迭代后 p 值进行排序.
基于这一思想,将整个系统抽象成一个有向图G = ( V,E) ,其中将 n 个部件抽象成网络节点,节点集合为 V,部件间关系抽象成有向边,有向边集合为E. 若链入部件 M 的故障节点是部件 V1,V2
,…,Vk,那么部件 M 的重要度为


系统部件间相关度分为影响度与被影响度.
1) 被影响度计算. 基于 pagerank 算法来计算系统部件的被影响度是基于以下假设:
假设 1 系统部件故障以概率 d 出现故障传递现象,即沿着故障传递模型进行传递,其中 0 <d < 1;
假设 2 当系统以概率 (1-d) 不沿故障链传递,那么下一个故障将以等可能概率发生于任何一个系统部件,系统部件的 CK值将会平均传递到各个系统部件;
假设 3 当系统部件 Vi能够将故障传递到部件M,部件 M 会获得故障相关被影响度 CK( M) ,传递值的大小依赖于部件 Vi的出度和其本身的 CK(Vi)值;
假设 4 如果部件容易受到其他 CK值较高的系统部件故障的影响,那么此系统部件的 CK值也会越高.

图 2 Pagerank 算法实现流程

2) 影响度计算. 在故障传递过程中,影响度是指系统部件能够对其他系统部件传递故障的能力,是与系统部件出度正相关的,记为 CI,节点出度越大,相应 CI值也越大. CI值代表了系统部件对其它部件产生故障影响的概率. 所以通过对邻接矩阵进行转置,借助 pagerank 算法可以求得系统部件故障相关影响度 CI.

2、 加工中心系统部件相关度评估
2.1 加工中心系统关联故障建模
加工中心系统功能关系如图 3 所示.

图 3 加工中心系统功能关系
加工中心系统及部件划分如表 1 所示.

表 1 加工中心系统故障部件划分
通过对某型加工中心现场故障数据分析,获得加工中心部分关联故障,其关联故障分析与统计如表 2、3 所示.

表 2 加工中心关联故障统计

表 3 加工中心关联故障分析
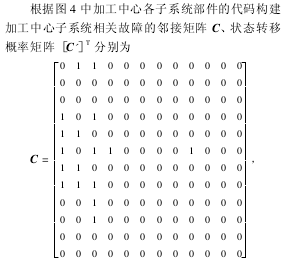
根据表 3 的加工中心关联故障分析构建故障传递关系模型如图 4 所示.

图 4 加工中心故障传递有向图模型
2.2 加工中心系统部件故障相关度评估


由表 4 和表 5 可知,进给系统、刀库和主轴系统的被影响度比较高,容易受其他子系统故障影响;气系统、润滑系统、液压系统、气动系统等子系统的影响度比较高,当这些子系统出现故障时容易影响其他子系统,对整个加工中心具有较强的危害性.
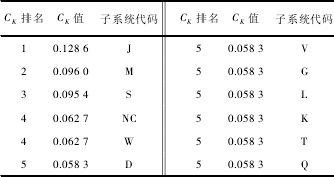
表 4 子系统 CK值及排序
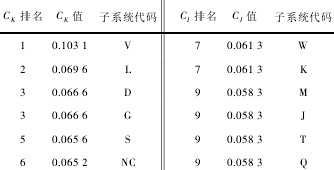
表 5 子系统 CI值及排序
3 、结 论
1) 故障相关度的大小与部件间故障关联关系成正比,存在故障相关关系的部件的故障相关度大于不存在故障相关关系的部件的故障相关度;
2) 故障相关度反映部件在故障传递中的位置.若部件被影响度大,影响度小,说明其是故障表象部件; 反之,影响度大而被影响度小的是故障源部件,这有助于故障诊断与维护.
3) 通过对某加工中心相关故障数据分析发现,进给系统、刀库和主轴系统的被影响度比较高,这些子系统属于执行机构,是故障表象子系统; 电气系统、润滑系统、液压系统、气动系统等子系统的影响度比较高,它们属于动力或控制系统,属于故障源子系统. 这与故障相关性定性分析结果一致,说明该方法是合理有效的.
4) 基于 Pagerank 算法的子系统相关度计算,能够定量评价系统部件故障相关度,为后续的系统部件故障率计算、可靠性评价及可靠性分配等研究奠定理论基础.
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com





