移动式救援机器人机械手臂的自适应控制问题
2017-7-26 来源:辽宁工程技术大学 作者:丛佩超 ,张欣
摘要:分析了移动式救援机器人系统参数存在误差时 ,其机械臂工作端轨迹的跟踪控制问题 。 首先基于雅可比矩阵概念与欧拉-拉格朗日方法,建立了移动式救援机器人系统的运动学与动力学模型。 然后,分析了系统的运动学与动力学模型存在误差时,对于逆动力学控制算法的影响,为了克服这种影响,引入了参数在线识别算法-自适应控制,设计了新的自适应-逆动力学控制算法 。最后 ,通过计算机数值仿真 ,验证了设计的自适应-逆动力学控制算法的有效性。
关键词:移动式救援机器人;雅可比矩阵;逆动力学控制;
自适应控制移动式救援机器人是机器人学的一个重要分支,由于能够在各种灾害发生时,替代救援人员完成相应任务, 近年来成为国内外众多学者研究的热点问题[1-4 ]。移动式救援机器人从广义上可分为地下、地面、水下、航空和航天移动式救援机器人。其中,地下、地面移动式救援机器人又可分为履带式、轮式、腿足式及仿人形机器人等。 移动式救援机器人系统主要由移动式基座(轮式/履带式)、机械手臂、导航系统、视觉系统、控制系统及辅助设备构成。在救援工作中,移动式救援机器人各种具体的操作动作是由其机械手系统完成的。因此,移动式救援机器人系统的机械手臂控制问题,在其众多关键技术中占有非常重要的地位。国内外学者对相关问题进行了大量的研究, 其中比较常见的控制算法有:PD 控制、PID 控制[5-6]、逆动力学控制、变结构控制、模糊控制[7-10]等。
这些控制算法应用的前提条件是: 移动式救援机器人系统及其操作目标的参数精确已知。一旦这一条件无法得到满足,传统控制算法的控制特性将出现较大偏差 (工作端轨迹跟踪出现较大误差)。为了解决上述问题,需要提出新的控制算法来加以克服。利用雅可比矩阵概念与变分法中的欧拉-拉格朗日方程, 分别建立了移动式救援机器人系统的运动学与动力学方程。基于得到的数学模型,进一步研究了移动式救援机器人系统参数存在误差时,其工作端轨迹跟踪控制问题,分析了此时传统控制算法控制特性所受到的影响。 为了解决这一影响,借助参数在线修正算法-自适应控制, 设计了自适应-逆动力学控制算法。 最后,通过计算机仿真验证了所设计控制算法的有效性。
1.移动式救援机器人系统的运动学与动力学模型
如图 1 所示, 移动式救援机器人系统主要由移动基座和机械臂组成。
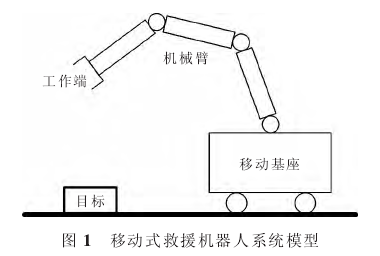
利用旋转矩阵、 齐次转换矩阵、D-H 转换法及雅可比矩阵概念, 建立移动式救援机器人系统的运动学方程,具体形式如下:

以方程(1)和方程(2)为基础,利用受非完整约束条件限制的 Lagrange 第二方程,推导出了移动式救援机器人系统的动力学方程:


2.系统参数误差对逆动力学控制算法的影响
对于移动式救援机器人系统的控制, 主要是通过方程(3)中的控制力项 f 来加以实现,各种不同的控制算法都体现在该力矩项中。 选择较为常用的一种控制算法———逆动力学控制算法来分析移动式救援机器人系统参数误差对于传统控制算法控制特性的影响。 逆动力学控制算法属于非线性控制算法范畴, 其通用形式如下[11]:


方程(8)是移动式救援机器人系统机械臂关节空间控制的误差方程。 方程(4)与方程(6)构成了移动式救援机器人系统机械臂的逆动力学控制算法。在移动式救援机器人系统开展救援工作过程中,
利用以上设计的逆动力学控制算法对系统的机械臂进行控制时,需要对系统参数精确掌握,一旦机器人系统所操作的目标参数未知,或系统自身某些参数未知,以上得到的逆动力学控制算法的控制性能将大打折扣,控制精度将无法得到保证。当移动式救援机器人系统出现建模误差、 计算误差和操作未知目标等情况时,逆动力学控制算法(方程(4))所依据的系统动力学模型(方程(3))将发生变化,此时,方程(4)变为:

表 1 为一个带两关节机械臂的移动式救援机器人系统的参数, 通过该表分析系统参数不确定性对于逆动力学控制算法的影响。 设移动式救援机器人的移动基座质量没有误差,精确已知。已知机械各关节质量分别为其真实值的 80%,利用方程(3)、方程(9)与方程(6),借助 MATLAB 软件进行移动式救援机器人系统的动力学仿真,仿真时间 T=8 s,仿真步长为 0.01 s。仿真结果如图 2、图 3 所示。
表 1 移动式救援机器人系统参数
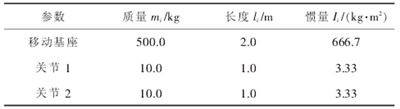
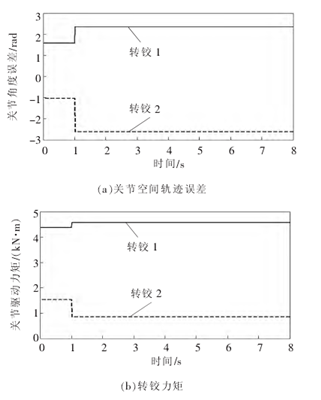
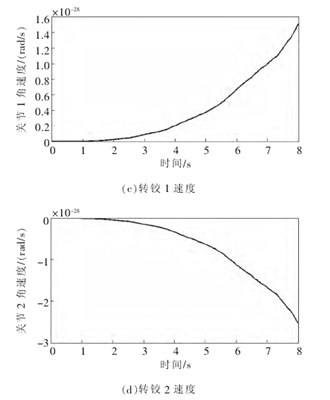
图 2基座移动时关节轨迹跟踪误差、各关节力矩、各转铰速度(m0=100 kg)
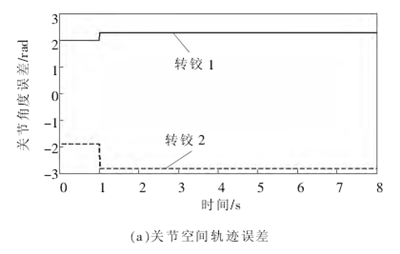
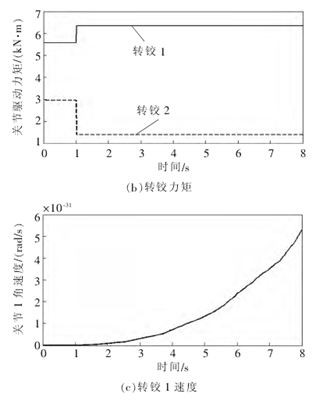
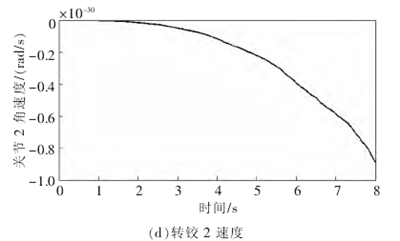
图 3基座移动时关节轨迹跟踪误差、各关节力矩、各转铰速度(m0=500 kg)
通过分析计算机仿真结果,可以得出以下结论:当移动式救援机器人系统工作时,由于各种原因,其自身的动力学参数出现误差, 传统的逆动力学控制算法的控制特性会出现较大偏差(如图 2、图 3 所示)。 在仿真开始阶段, 机械臂关节空间期望轨迹的跟踪误差稳定在一个较大值附近; 机械臂的驱动力矩保持在 6~7k N·m 之 间 ,这种情况对于驱动电机非常有害 ;与此同时,机械臂各关节转速也在不断增大。
3.自适应-逆动力学控制算法
文中分析得到了移动式救援机器人系统参数存在误差时,逆动力学控制算法的控制特性偏差。为克服这一偏差,首先要找到出现这种控制偏差的原因。将方程(9)代入到方程(3)中得:
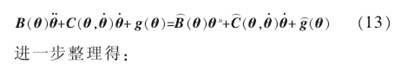

式(17)表示的 σ项就是移动式救援机器人系统的动力学参数误差项。正是由于它的存在,引起了逆动力学控制算法控制特性的偏差。 研究的自适应控制算法的控制目标是:利用参数在线修正原理,消除不确定项σ对逆动力学控制算法的影响。移动式救援机器人系统的动力学方程可化为如下线性形式[11]:


方程(24)是移动式救援机器人系统新的关节轨迹误差方程。当这一条件成立时,系统参数误差对于控制算法控制特性的影响消失。 因此,设计新的自适应-逆动力学控制算法的关键是找到合适的自适应率, 以满足上述条件的成立。利用李雅普诺夫判据来确定自适应控制算法的参数自适应率。 首先,选取李雅普诺夫函数为:


4.仿真验证
仍以表 1 中给出的移动式救援机器人系统模型为例,利用设计的自适应-逆动力学控制算法,对其进行计算机仿真。 仿真时间 T=5 s,仿真步长为 0.01 s,仿真结果如图 4、图 5 所示。
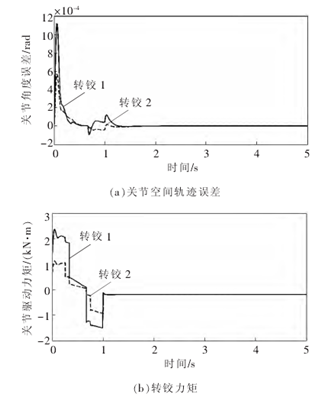
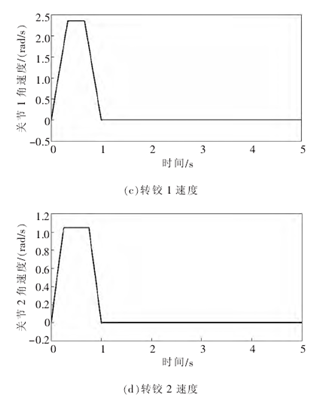
图 4基座移动时关节轨迹跟踪误差、各关节力矩、各转铰速度(m0=100 kg)
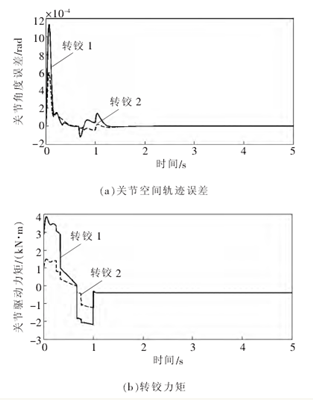
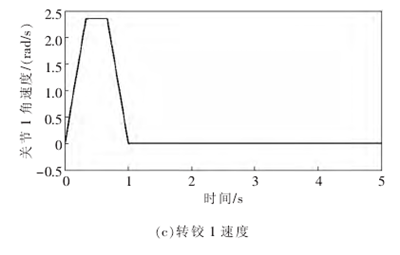
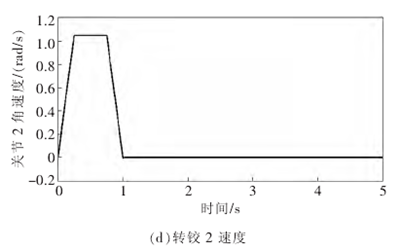
图 5基座移动时关节轨迹跟踪误差、各关节力矩、各转铰速度(m0=500 kg)
将以上仿真结果与图 2、图 3 的结果进行对比,可以得出如下结论:采用设计的自适应-逆动力学控制算法,无论移动式救援机器人系统的移动基座质量小还是大, 关节轨迹跟踪误差均被控制在微小值之内;与此同时,机械臂各关节的速度、 驱动力矩也均被控制在合理的范围之内,有效地保护了机械臂各关节转角及其驱动电机。因此, 该控制算法有效地消除了系统动力学模型误差对于逆动力学控制算法控制特性的影响。
5.结论
研究了移动式救援机器人系统存在参数误差时,其机械手臂的自适应控制问题,得到如下结论:(1)基于系统的运动学与动力学模型,设计了逆动力学控制算法, 并分析了系统参数误差对于该控制算法的影响,具体的影响表现为:轨迹跟踪误差出现较大偏差,转铰速度和驱动力矩变大。(2)针 对上述问题 ,借助自适应控制算法思想 ,将传统的逆动力学控制算法与自适应控制算法相融合,设计了全新的自适应-逆动力学控制算法,该算法有效地消除了移动式救摇机器人系统参数不确定性对于逆动力学控制算法的影响。(3)通过计算机仿真实例,验证了控制算法的有效性。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息





