工业机器人位姿误差空间 IDSW 插值补偿方法研究
2017-7-11 来源:江苏无锡 作者:陈宵燕 张秋菊 孙沂琳 陈海卫
在焊接、激光切割、自动化装配等实际生产和应用中,机器人精度是衡量其性能的重要指标[1]。 一般而言,工业机器人具有较高的重复定位精度,而绝对定位精度较差,前者可达到0.1 mm人,而后者一般2~3 mm,无法满足某些行业的生产要求。
目前提高绝对定位精度的方法主要分为两种[2]:误差预防法和误差补偿法。 前者主要是通过提高机器人设计和加工精度,这种方法不仅成本高而且不易实现。 后者也可称为机器人标定,该方法通过使用先进的测量技术并且成功辨识出所建机器人模型中各项参数的准确值,然后通过修改机器人控制器中的参数或者增加一定的控制算法以达到提高定位精度的目的。 机器人标定是离线编程技术实用化的关键技术之一,其最后一步且关键一步为误差补偿[3],现阶段误差补偿方法主要分为:基于模型的方法[4-7]和基于插补的方法[8-9]。
基于模型的补偿方法的基本原理是:在假设主要误差源为关节轴倾斜和关节偏移等几何误差的情况下,用机器人运动学模型来描述机器人位姿误差。校准中要进行机器人模型参数对测量姿态误差的拟合,用校准后的机器人模型预测各个位姿的误差。基于模型的补偿方法主要分为两种[10]:
1) 关节空间补偿。 利用标定后的结果直接在关节空间修正,对于某可达位姿,重新计算其关节值,来达到提高机器人位姿精度的目的;
2) 微分误差补偿。该方法一般是针对基于微分变换思想建立机器人误差模型,识别几何参数名义值与真实值之间的微小偏差,并把其补偿控制器的名义参数上,达到提高机器人精度的目的。
基于模型的方法缺点是需建立复杂的运动学误差模型,并需修改各项运动学参数从而造成机器人运动学逆解的困难,计算复杂且难以实现。
对于基于插补思想的误差补偿法,需要对机器人末端在机器人工作空间中的特定网格点的位姿进行测量,目前多数采用在工作空间用双线性插补和多项式拟合等插补技术来拟合相应于不同定位误差的关节补偿指令。 此外,文献[9] 提出一种空间插值法,该方法在前期将机器人工作空间划分成的网格,对网格点进行位置误差测量,然后采用空间插值来补偿定位误差。 但这种方法存在很多缺陷,目前只在没有考虑姿态变化对位置误差的影响下对位置误差进行了补偿,且没有对姿态误差进行补偿,因此存在很大的局限性。
随着高精度测量工具的不断发展及普及应用,如FARO 激光跟踪仪、LEICA 激光跟踪仪等,使得基于插补的补偿方法变得更为便捷、可靠,同时,完善并优化基于插补的补偿方法也变得更为重要和紧迫。 针对空间插值补偿方法,对机器人位姿误差与其末端位置之间相关性进行探讨,提出基于均匀数据场的空间IDSW 插值算法的机器人位姿误差补偿方法,并设计对比试验,利用 MATLAB 进行仿真,结果证明该方法对机器人位姿精度提高的有效性。
1.机器人运动学误差模型
DH 模型常用来对机器人空间的位姿进行表示和建模,这个建模方法由 Denavit 和 Hartenberg 两人创新性提出的。 该建模方法优点在于其非常简单且通用性非常好,可对任何构型的机器人的连杆和关节进行建模,方法为
Ai=Rot(z,θi)Trans(0,0,di)Trans(ai,0,0)Rot(xi,αi) (1)
对于六自由度的串联机器人,其末端的位置和姿态的坐标变换为
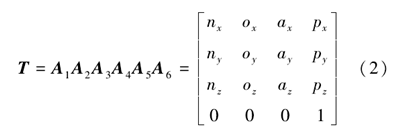
经典的 DH 模型存在参数不连续的缺点:假如相邻关节轴线实际上不平行而理论上却以平行来建模,则这两个轴线间的相对位置误差的建模将不能满足“小误差建模” 条件,造成参数突变。 “小误差模型”定义如下:对于连杆坐标变换的微小位姿误差能通过连杆参数的微小偏差对其进行建模[11]。
为了解决这种问题,Hayati 等[12]在经典 DH 运动学模型的基础上,增加了一个新的绕y 轴的旋转参数 βi,该模型被称之为 MDH 模型。 该模型的相邻连杆坐标变换的数学表达式为
Ai=Rot(z,θi)Trans(0,0,di)Trans(ai,0,0)Rot(xi,αi)Rot(yi,βi) (3)
机器人定位精度误差大体可以分为两类:运动学(几何)参数误差和动力学(非几何)参数误差,具体包括几何参数的偏差、关节偏移、连杆和关节的柔性、齿轮系结构、齿轮间隙、环境温度等等。 运动学参数误差主要由制造和装配的误差造成的,所导致的误差占总误差的 80%左右[13]。 所建立的机器人运动学误差模型,主要考虑运动学参数误差对机器人位姿误差的影响。 除了以上运动学参数存在的误差,在建立位姿误差模型时,测量机器人末端实际位姿将引入机器人基坐标系相对于机器人构造的基坐标系之间的误差 Δσ。 采用微分法[11]建立机器人运动学误差模型,对式(3)进行全微分,得
dAi=∂ANi∂θiΔθi+∂ANi∂diΔdi+∂ANi∂aiΔai+∂ANi∂αiΔαi+∂ANi∂βiΔβi ( 4 )
式中: Δθi、Δdi、Δαi、Δai、Δβi分别表示连杆长度偏差、连杆偏置、扭角偏差、关节角偏差和相邻平行轴的角度偏差。
由于该方法较成熟,在此对过程不做赘述,具体可参见文献[11],最终所建立的运动学误差模型为
E = J·ε(5)
式中:E 为位姿误差;J 为辨识雅克比矩阵;ε 为运动学参数误差。
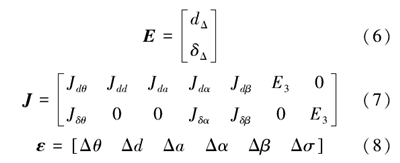
2 定位位姿误差模型
2.1 机器人位姿误差与末端位置相关性
空间插值是指通过已知的数据点或已知的已划为各个相对小一些的区域内的数据点,计算出相关的其他未知点或相关区域内的任意点的方法[14]。 研究的空间IDSW 插值补偿法是基于笛卡尔坐标系下的空间插值,即选择一定数量的机器人末端位置作为测量点,测量这些点所对应的位姿误差,根据这些已知点所对应的位姿误差来计算相关区域内其它任意位置的位姿误差。 由此可知,机器人位置和机器人位姿误差两者之间的高相关程度是本文插值补偿法有效的先决条件。
Pearson 相关(也称为积差相关或积矩相关) 是英国统计学家皮尔逊于 20 世纪提出的一种计算直线相关的方法。 Pearson 相关系数用来衡量两个数据集合是否在一条线上面。 其计算公式为
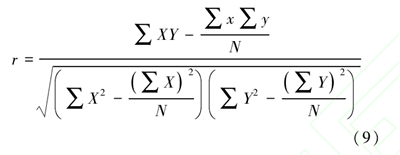
式中相关系数 r 的值介于-1 与+1 之间。
相关系数性质如下:
1) 当r >0 时,表示两变量正相关,r <0 时,两变量为负相关;
2) 当| r | =1 时,表示两变量为完全线性相关,即为函数关系;
3) 当r =0 时,表示两变量间无线性相关关系。
一般可按三级划分:| r | <0.4 为低度线性相关;0.4 ≤| r | <0.7 为显著性相关;0.7 ≤| r |<1 为高度线性相关。 低度线性相关又 可 分为 弱 相 关(0.2~0.4)和极弱相关或无相关(0.0~0.2)。
利用 Pearson 相关系数来衡量机器人位置和机器人位姿误差之间的相关性程度。以 Staubli TX60L机器人为例,根据第 1 节所述方法建立运动学误差模型,可知机器人的位置误差和姿态误差都是机器人关节角 θi的函数,由于姿态误差数量级较位置误差小,所以将位姿误差分为位置误差和姿态误差,并分别进行分析。
利用 MATLAB 仿真功能,设计实验 1,其步骤如下:
1) Staubli TX60L 机器人名义运动参数及设定的运动参数偏差值如表 1 所示,利用蒙特卡洛法随机选取 101 组 6 个关节角度值,记录其所对应的101 组机器人末端位置值。
表 1 Staubli TX60L 机器人运动参数名义值和偏差值
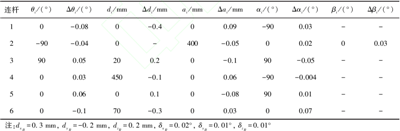
2) 将这 101 组关节值代入式(5),计算其对应的位置误差 dΔ和位姿误差 δΔ。
3) 计算第 1 组数据所对应的位置误差dΔ和位置值分别与其它 100 组对应的置误差dΔ和末端位置值的位置误差差值 ΔdΔ和位置值差值 dz,利用MATLAB 得到 ΔdΔ和 dz的两者的相关性(用散点图表示,见图 1)和 Pearson 相关系数r1;
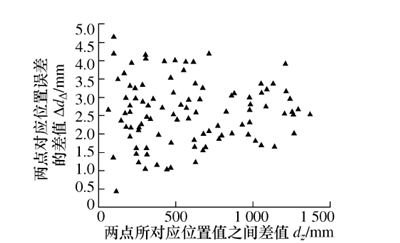
图 1 两点的位置误差差值与dz相关性
4) 计算第 1 组数据所对应的姿态误差δΔ和位置值分别与其它 100 组对应的位姿误差δΔ和末端位置值的姿态误差差值 ΔδΔ和位置值差值 dz,利用MATLAB 得到 ΔδΔ和 dz的两者之间的相关性(用散点图表示,见图 2)和 Pearson 相关系数r2;
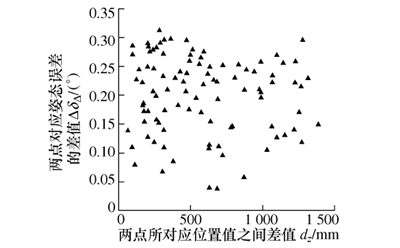
图 2 两点的姿态误差差值与dz相关性
利用 MATLAB 计算得到 ΔdΔ和 dz的 Pearson 相关系数 r1= 0.015 7, ΔδΔ和 dz的 Pearson 相关系数r2= -0.079 2。 图 1 所描述的两点所对应的位置误差之间的差值与位置值间的差值不具有明显的关系,根据计算所得相关系数r1可知两变量的线性关系几乎为无相关。 图 2 所示两点所对应的姿态误差之间的差值与位置值间的差值也不具有明显关系,同时根据所得的相关系数r2可知其线性关系也几乎为无相关。 而对机器人来说,末端执行器的位姿由位置和姿态共同决定,所以在研究机器人位置和机器人位姿误差两者之间的相关性时,存在一个可控变量———姿态。 因此,设计实验 2,其步骤如下:
1) 利用蒙特卡洛法选取 Staubli TX60L 机器人工作空间 101 组机器人末端位置值,记录其所对应的101 组机器人位置值,任意选取某一姿态,在该姿态下,对上述 101 个位置经运动学逆解得到 101 组6 个关节角度值;
2) 同实验 1 的步骤 2);
3) 同实验 1 的步骤 3),亦利用 MATLAB 得到ΔdΔ和 dz的两者之间的相关性(用散点图表示,见图3 所示)和 Pearson 相关系数r3;
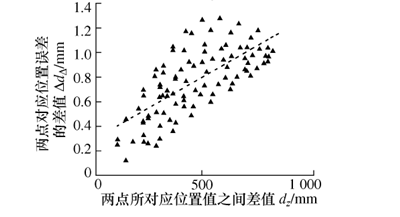
图 3 两点的位置误差差值与dz相关性
4) 同实验 1 的步骤 4),亦利用 MATLAB 得到ΔδΔ和 dz的两者之间的关系图(用散点图表示,如图4 所示)和 Pearson 相关系数r4。
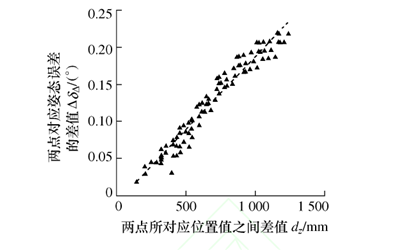
图 4 两点的姿态误差差值与dz相关性
利用 MATLAB 计算得到 ΔdΔ和 dz的 Pearson 相关系数 r3为 0.73,ΔδΔ和 dz的 Pearson 相关系数r4为 0.98。 比较图 1 和图 3,并根据所求的相关系数r1和 r3,可知通过控制机器人末端姿态这一变量后,两点对应的位置误差间的差值与位置值间的差值之间呈高度线性相关;分析比较图 2 和图 4,并根据所求的相关系数 r2和 r4,可知在机器人末端姿态不变的情况下,两点对应的姿态误差间的差值与位置值间的差值之间呈高度线性相关。 综上所述,在机器人的工作空间内,若机器人末端姿态保持一致,则两点所对应的位置值的差值 dz越大,所对应的位置误差差值 ΔdΔ和姿态误差差值 ΔδΔ也越大,且两者关系均呈高度线性相关。 而此时,所提出的空间 IDSW插值补偿法对机器人位姿误差补偿有效的前提条件成立。
2.2 姿态变化因素下的定位位姿误差模型
根据 2.1 节的结论可知,为使空间 IDSW 插值补偿方法能对机器人位姿误差补偿在任意姿态下均有效,必须考虑姿态变化对位姿误差的影响。 所以将重点研究如何建立固定位置时姿态变化因素下的定位位姿误差模型。
机器人运动姿态的有两种常用描述方法:机械人末端的运动方向和绕轴 x,y,z 的旋转序列(欧拉角)。 前者是关于机器人运动学模型计算得到接近矢量 a,方向矢量n,法线矢量o,即式(2) 机器人末端坐标系变换矩阵的旋转矩阵对应的 3 个列矢量;后者是笛卡尔坐标空间下,对机器人位置控制时运动姿态的 3 个重要参数,一般工业机器人的姿态表示法采用的是 x_y_z 欧拉角,即欧拉角Φ,θ,φ。 这种描述在基坐标系{B} 的方位的法则如下:基坐标系{B} 与参考系{A} 相同,首先使{B} 绕xB轴转 Φ 角,然后绕yB轴转 θ 角,最后绕zB轴转 φ 角,如图 5 所示。
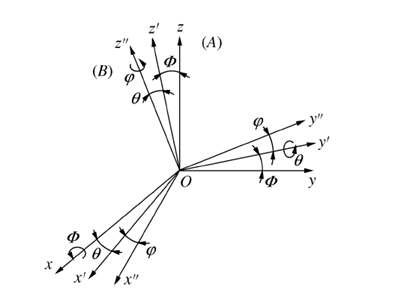
图 5 x⁃y⁃z 欧拉角法则
根据右乘的原则,可以求得与之等价的旋转矩阵,即(图片)
由此可知,给定x-y-z 欧拉角 Φ,θ,φ, 便可确定对应的旋转矩阵。当给定旋转矩阵,也可求出等价的x-y-z 欧拉角Φ,θ,φ。 令
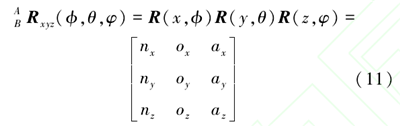
由上述可知,绕zB轴转 φ 角只影响方向矢量 n和法线矢量 o,与接近矢量a 无关,同时经研究可知旋转角 φ 对位姿误差的影响呈三角函数关系。 因此,对固定位置时姿态变化的定位位姿误差模型确立分为两步:正弦函数相位角偏移误差建模和矢量夹角加权平均误差建模。
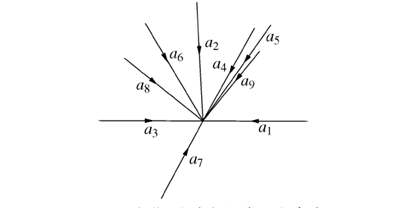
图 6 定位下所选取的 9 个姿态
首先对机器人姿态操作空间以接近矢量划分,令 φ =0 只考虑欧拉角 Φ 和 θ,选取 9 个具有代表性的姿态,如图 6 所示。 其次就是考虑欧拉角φ 对机器人位姿误差的影响,对以上9 个姿态分别测量3 个不同欧拉角 φ 时的位姿误差,建立正弦函数,即
A = B*sin(φ - w)- C (12)
由此得到任意欧拉角φ时这9个姿态所对应的位姿误差,这就是正弦函数相位角偏移误差。
对机器人的其他操作姿态所对应的位姿误差可利用矢量夹角加权平均求得。 根据如图 6 所示的已知 9 个姿态的每个姿态均有相对应的接近矢量、方向矢量和法线矢量,与所求姿态所对应的接近矢量、方向矢量和法线矢量分别进行夹角算,选取夹角量最小的 3个姿态并根据第一步获得该 3 个姿态对应的位姿误差来进行量夹角加权平均计算,得到该姿态下的位姿误差。 综合上述两步,就是建立的在姿态变化因素下的定位位姿误差模型为
E′ =∑3i =1E(i)× λi ( 1 3 )
式中:E(i) 为 9个代表性姿态经第一步获得所求姿态下对应的位姿误差;λi为矢量夹角加权值。
3 空间IDSW 插值补偿模型
对机器人位姿误差补偿是基于空间插值法,空间插值方法很多。 依据空间插值的基本假设和数学本质可分类为:几何方、统计方法、空间统计方法、函数方法、随机模拟方法、物理模型模拟方法和综合方法[15]。 几何方法包括反距离加权法、泰森多边形法等;统计方法包括趋势面、多元回归法和多面函数法等;空间统计方法包括克里金法、最小二乘配置和杨赤中法等;函数方法包括样条函数、双线性内插方法[16]。 所提出的空间 IDSW 插值补偿法选择的是反距离加权法来进行机器人位姿误差插值补偿,该算法是以距离作为权重的滑动平均加权插值法[17],它是根据离散点生成规则网格数据最常见的空间内插方法,计算过程简单且运算速度快。
根据第 2.1 节的研究结果可知,当机器人末端姿态一致时,其末端任意两点所对应的位置误差间的差值 ΔdΔ和姿态误差间的差值 ΔδΔ分别与该两点位置间的差值 dz具有高度的线性相关性。 根据第2.2 节所建立的定位位姿误差模型,可以将所测量点(即已知点) 的姿态所对应的位姿误差转换到需要预测的位姿的姿态所对应的位姿误差,使得机器人末端姿态保持一致的条件成立,满足了第 2.1 节所提出的空间插值补偿法有效性的先决条件,从而为空间 IDSW 插值算法在机器人位姿误差补偿上奠定了理论基础和应用基础。
根据采集点的分布可以采集数据分为规则采集点数据集点和离散采集点数据集。 前者可使反距离加权算法具有更好的逼近程度,本文将对机器人操作空间的规则采集点数据集称为均匀数据场。 因此,将机器人的工作空间划分为均匀网格,而对于某一目标点 M,使用快速搜索法得到距离M 点最近的8 个包络点,如图 7 所示。
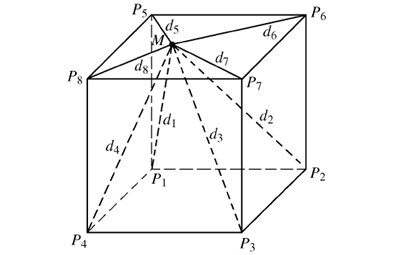
图 7 基于反距离加权算法的位姿补偿原理
利用反距离加权法[18-19],可得位置误差和姿态误差的补偿模型为:
d∗Δ=∑8i =1dΔ(i)× ρi(14)
δ∗Δ=∑8i =1δΔ(i)× ρi(15 )
式中:d*Δ和 δ*Δ为目标点的预测位置误差和姿态误差;dΔ(i)和δΔ(i)为目标点周围 8 个包络点的位置误差和姿态误差;ρi为 8 个包络点的权重,权重的公式为
ρi=1dki∑8j =11dkj(16)
式中:di或 dj为目标点与周围 8 个包络点之间的距离;k 为幂指数。
在式(16)中,k 值越大,插补结果越具有平滑,当取 k= 2 时, 通常称为反距离 平 方 加 权 ( 简 称IDSW)算法。 因此,在基于空间插值的反距离平方加权算法下,提出机器人位姿误差空间 IDSW 插值补偿方法,上述所建立的补偿模型即为基于均匀数据场的空间 IDSW 插值补偿模型。
4 仿真验证
为验证空间 IDSW 插值算法对机器人位姿误差补偿的有效性,将利用目前较为成熟的微分误差补偿法与本文所提出的方法进行对比试验。 微分误差补偿法即基于位姿误差模型,将辨识得到的参数偏差来修正名义参数,来达到误差补偿效果。
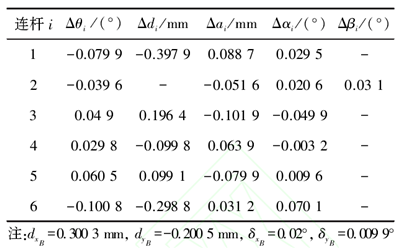
在本文第 2 节中,以 Staubli TX60L 机器人为例已建立了运动学位姿误差模型,然后对辨识雅克比矩阵进行 QR 分解,剔除两个无法辨识的参数:dZB和 δZB, 再使用最小二乘法对其余 28 个参数进行辨识,结果如表 2 所示。 最后将该辨识得到的参数偏差用于基于微分误差补偿法补偿实验。
表 2 最小二乘法参数辨识结果
基于空间 IDSW 插值算法的机器人位姿误差补偿方法首先需要建立合适的空间网格,将 StaubliTX60L 机器人的某局部工作空间划分为均匀网格,令网格边长为 100 mm,以机器人末端的笛卡尔坐标系来划分,X 轴向工作范围为(300 mm~500 mm),Y轴向工作范围为( -400 mm ~ 400 mm),Z 轴向工作范围为( -100 mm ~ 200 mm),具有 48 个网格,108个网格顶点。仿真实验如下:利用 MATLAB 建立基于 MDH模型的 Staubli TX60L 机器人运动学模型,并编写空间 IDSW 插值算法和递归搜索算法;选取 3 个不同姿态,分别在这 3 个姿态下,在网格空间中任取 3 个点,共 9 个选取的验证点如表 3 所示。 利用表 1 预定义的运动参数的偏差值,修改运动学模型的参数,分别计算这 9 个点所对应的位置误差和姿态误差,结果分别见图 8和图 9。
表 3 选取的验证点
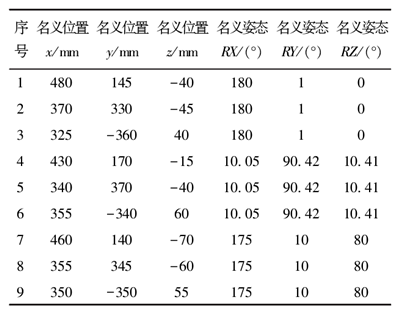
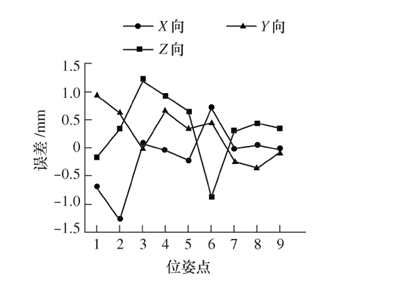
图 8 补偿前位置误差
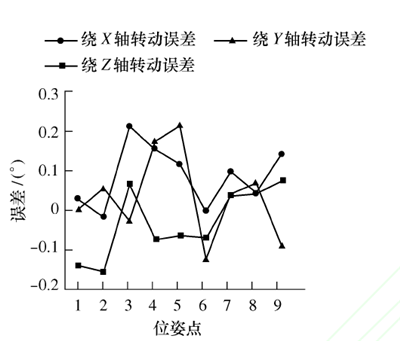
图 9 补偿前姿态误差
分别计算 108 网格顶点在如上 3 个姿态下所对应的位置误差和姿态误差,所得误为采集点数据集,用以建立空间 IDSW 插值算法所需的均匀数据场;分别根据微分误差补偿法(图中简称微补法)和空间 IDSW 插值算法(图中简称 IDSW 法)对机器人位姿误差进行补偿,其结果如图 10 和图 11 所示。
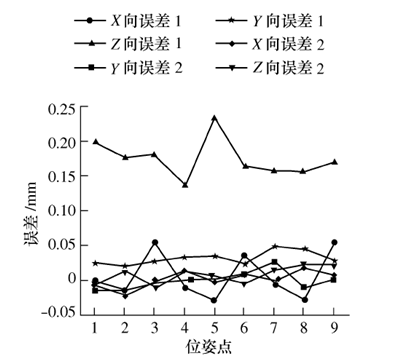
图 10 微补法和 IDSW 法补偿后的位置误差 1 和 2
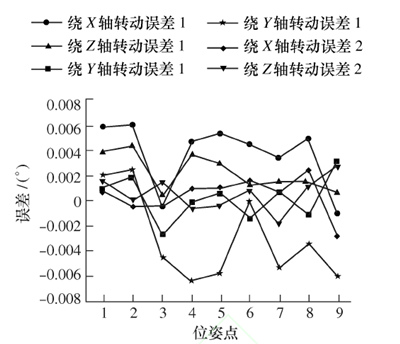
图 11 微补法和 IDSW 法补偿后的姿态误差 1 和 2
根据 MATLAB 仿真实验结果,在 3 个不同姿态下, 微 分 误 差 补 偿 法 补 偿 后 位 置 精 度 平 均 提84.8%,83.1%,59.4%,姿态精度平提高 95.9%,96.6%,94.6%;而经反距离平方比加权算法补偿后位置精度平均提高 98.0%,98.5%,93.5%,姿态精度平均提高 98.7%,98.5%,97.3%。 所以采用微分误差补偿法和空间 IDSW 插值算法对位姿误差都具有较好的补偿效果。 分析图 10 和图 11 可知,空间IDSW 插值算法对位置补偿效果优于微分误差补偿法,同时姿态补偿效果也优于微分误差补偿法。 因此,所提出的补偿方法补偿效果更好,且不需要建立复杂的机器人位姿误差模型,不需要进行繁琐的参数辨识过程。 综上所述,经 MATLAB 的对比实验仿真验证,在只考虑运动学参数偏差引起的位姿误差情况下,所提出的插值算法对机器人位姿误差补偿是有效的。
5 结论
在探讨机器人误差补偿的现有方法之上,研究基于空间插值的补偿方法,并提出机器人末端位置与机器人末端位姿误差的相关性程度是决定插补补偿方法是否有效的充分条件。 首先利用 Staubli TX60L 的DH 参数建立运动学模型,并预定义各项运动参数的偏差值,使用 MATLAB 建模仿真分析,得到当机器人末端姿态不变时,任意两点对应的位置误差之间的差值和姿态误差之间的差值分别与两点间的位置差值具有高度线性关系。 然而机器人末端任意姿态时,两点的位置误差的差值和姿态误差的差值分别与两点间的位置差值之间几乎无关。 因此,提出了一种姿态变化因素下的定位位姿误差模型。 最终提出机器人位姿误差空间 IDSW 插值补偿方法,并由 MATLAB 仿真验证了该补偿方法的有效性。
所提出的位姿误差补偿方法最大的优点是不需要建立机器人位姿误差模型,也不需要辨识机器人复杂、冗余的各项参数,在测量上也只需要有限的采集点,尤其是对在机器人操作时末端执行器具有任意姿态且对姿态要求高的机器人应用领域具有较好的应用前景,
该方法具有计算过程简单、速度快、补偿效果好等优点。 基于空间 IDSW 插值算法是一种空间内插方法,只能对网格空间内的数据进行补偿,所以需探索扩展方法,研究具有外推能力的插值方法将是后续的研究工作。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com





