复杂曲面五轴数控无干涉刀轴规划
2020-12-29 来源:南京工业大学机械与动力工程学院 作者:濮潇楠,刘旭,凌祥
摘 要:五轴数控被广泛应用于复杂曲面零件的加工制造,丰富的刀轴姿态是五轴数控的优势,但干涉避让是刀轴规划的难点。将复杂曲面零件离散为点云模型,在任一刀触点处建立初始刀轴空间,计算初始刀轴与曲面离散点的间距,识别无干涉刀轴空间。针对无干涉刀轴空间为空集的刀触点进行干涉刀轴修正,并利用投影法优化计算效率。加工结果表明建立的五轴数控刀轨可实现加工干涉,同时投影法有效减少参与干涉检测检测额的曲面离散点数量,提高计算效率。
关键词:复杂曲面;五轴加工;点云模型;无干涉刀轴
1、引言
随着 CAD/CAM 技术的发展,复杂曲面零件被广泛应用于能源、化工、航空航天等领域,制造此类零件常选用五轴数控加工。相较于传统的三轴加工,五轴数控技术可以提供更丰富的刀具姿态,增加刀具的加工范围,减少反复装夹产生的人为误差。但丰富的刀具姿态增加了刀轴规划的难度,刀轴矢量沿刀轨不断变化,刀具易与工件发生干涉。加工干涉可分为局部干涉和全局干涉两种,局部干涉是指刀具端部出现过切,全局干涉是指刀杆和工件等发生碰撞。干涉现象不仅会降低零件质量,还可能使刀具断裂失效。因此,加工过程无干涉是优质五轴数控刀轨的重要指标。对于局部干涉,刀具直径是避免干涉的关键因素,文献利用遗传算法确定避免局部干涉的最佳刀具尺寸。对于全局干涉,研究重点在于判断刀具柱面和工件表面是否相交。文献通过离散 B 样条来判断复杂曲面相交,文献利用包围盒刀具模型和八叉树工件模型来进行干涉检测。文献利用可视锥方法生成无干涉刀轨,文献将可视锥与刀具可达方向锥相结合,减少计算时长。为进一步提高计算效率,文献采用显卡计算的可视图来规划无干涉刀轴,文献根据无干涉刀轴空间确定装夹工件的最佳方位。复杂曲面的精加工刀具多为球头刀,其加工干涉多为全局干涉。随着加工要求的不断提高,刀轴矢量所受的约束逐渐增加。利用点云模型建立无干涉刀轴空间,为后续刀轴规划奠定基础。
2、无干涉刀轴空间
在数控程序中,刀轨曲线被视为一系列刀触点。为保证整体刀轨无干涉,需确定任一刀触点的无干涉刀轴空间。球头刀在任一刀触点处的旋转中心为刀位点,因此初始刀轴空间可视为以刀位点为圆心,刀具杆长为半径的球状空间。初始刀轴空间内包含无数的刀轴矢量,无法依次对其进行干涉检测。为从初始刀轴空间内提取无干涉空间,可根据曲面法向建立等间距的阵列平面和等夹角的旋转平面,两组平面与初始刀轴空间的球面相交生成的经纬曲线,将经纬线交点与刀位点的连线作为待测刀轴,如图 1所示。待测刀轴将初始刀轴空间离散为锥状子区域,若存在待测刀轴与工件产生干涉,则认为相邻子区域是干涉的;若标识子区域的待测刀轴均满足无干涉要求,则认为该区域内的刀轴矢量是可行的。
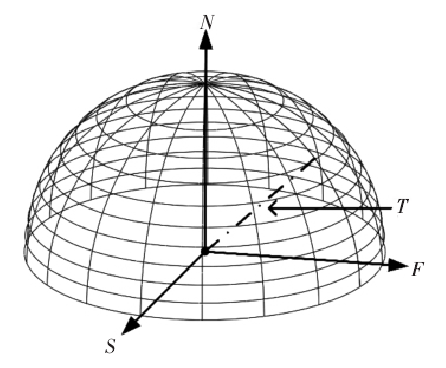
图1:初始刀轴空间
2.1、全局干涉检测
为判断待测刀轴是否发生干涉,需对其进行干涉检测。干涉检测的本质是计算刀轴矢量与工件表面的间距,而复杂曲面难以用解析公式直接表示。为解决该问题可利用三角网格离散工件表面,提取网格节点生成加工曲面的点云模型,计算待测刀轴矢量与任一曲面离散点的间距即可实现干涉检测。假设刀位点为 PC(x1,y1,z1),刀具端点为 PE(x2,y2,z2),被检测的曲面离散点为 PS(x3,y3,z3),如图 2 所示。
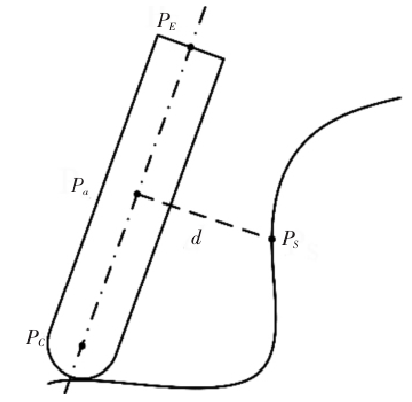
图2:干涉检测
刀轴上的点可表示为 Pa(xa,ya,za):
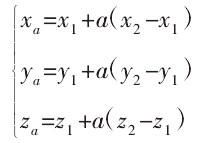
其中,a>0,Pa与曲面离散点 PS的距离可表示为:
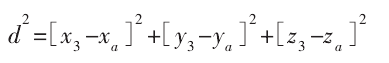
为检测干涉,需计算 d 的最小值,此时式(2)满足:
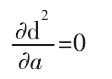
根据公式(3)可计算参数 a:
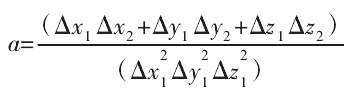
其中,△x1=x2-x1,△y1=y2-y1,△z1=z2-z1
将式(4)代入式(2)~式(3)即可计算刀轴矢量与曲面离散点的间距,遍历初始刀轴空间内的曲面离散点,提取待测刀轴矢量与曲面离散点的最小间距。若最小间距小于刀具半径,则表示该刀轴矢量下刀具会与工件发生干涉;反之则说明刀轴矢量无干涉。依次检测所有的待测刀轴矢量,提取由无干涉刀轴矢量标识的子区域,构建单个刀触点的无干涉刀轴空间。
2.2、干涉刀轴修正
在构建无干涉刀轴空间的过程中,待测刀轴矢量间存在一定间距。若刀触点位于较为封闭的区域,此时无干涉刀轴空间可能为空集,为避免该现象需对已知的干涉刀轴矢量进行修正。将与刀轴矢量发生干涉的曲面离散点标记为干涉点,若刀具与工件发生严重干涉,则相应的刀轴矢量必然拥有大量的干涉点;反之干涉点的数量较少。从干涉刀轴空间内提取干涉点最少的刀轴矢量,将其作为修正目标 T。修正干涉刀轴,如图 3 所示。
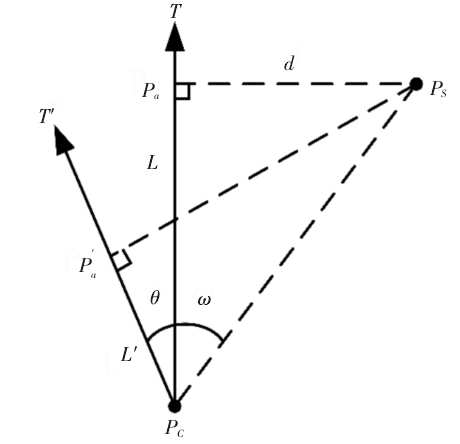
图3:修正干涉刀轴
提取与干涉刀轴 T 最近的曲面离散点 Ps,建立的修正平面,如图 3 所示。Pa和 Pc的距离为 L,干涉刀轴和曲面离散点的夹角ω 可表示为:
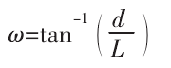
若完成刀轴修正,曲面离散点 Ps与修正刀轴 T′的间距可表示为 R+ε,R 表示刀具半径,ε 表示刀具和工件间的微量间距,避免修正后的刀具和工件临界接触。此时 P′a和 Pc间的距离L′可表示为:
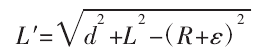
修正角度 θ 可表示为:
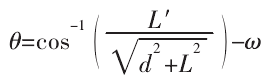
将干涉刀轴 T 和曲面离散点 Ps的夹角增加 θ 即可生成修正刀轴 T′,修正后的刀轴矢量仍需进行干涉检测,避免修正过程产生新的干涉点。若存在新的干涉点,可重复上述步骤直至生成无干涉刀轴。为避免陷入无限循环,可限制循环次数,若多次循环后仍无法生成无干涉刀轴,可减少刀具直径以增加刀具和工件的间距。
2.3、投影法优化
在上述算法中,参与检测的曲面离散点数量是决定计算效率的关键。若减少离散密度会降低干涉检测的精度,因此需在保持离散密度的前提下减少参与检测的曲面离散点。投影法是识别潜在干涉区域的有效手段,若刀轴矢量引发干涉,离散点必然侵入刀具内部,此时离散点投影被刀具投影覆盖,如图 4 所示。
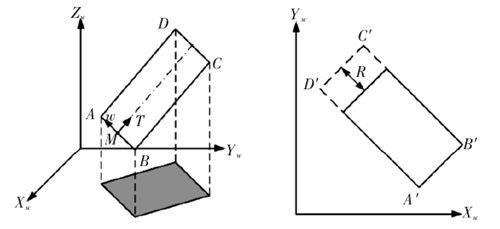
图4:刀具投影
在工件坐标系(Workpiece Coordinate System)内选取 XwYw面作为投影平面,Zw轴负向为投影方向。为简化刀具投影的计算过程,可将刀具表示的矩形面,如图 4 所示。M 为刀心点,T 为刀轴矢量,w 与 T 正交同时平行于 XwYw平面。AB 间距为刀具直径,BC 间距为刀具杆长,矩形面四点坐标可分别表示为:
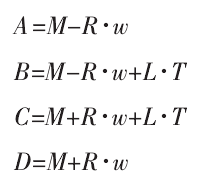
将四点的 Zw轴坐标设为 0 即可获得刀具在 XwYw平面内的投影 A′B′C′D′,但该投影忽略了刀具端面的影响。为提高计算精度,可将刀具投影沿刀轴方向延伸 R 个单位长度,增加投影的覆盖面积。若曲面离散点的投影 P 位于刀具投影之内,P 点必然满足:
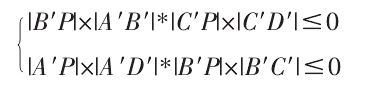
位于刀具投影内的曲面离散点是潜在的干涉区域,需进行干涉检测;刀具投影外的曲面离散点不必参与干涉检测。
3、刀轴光顺优化
在实际加工中,刀轨不能从无干涉刀轴空间内任意选用刀轴矢量,因为刀轴整体需具备良好的一致性,避免刀轴突变,保持机床稳定运动。为实现上述目标,需对刀轴进行光顺优化。将无干涉刀轴空间最小的刀触点作为刀轴规划的起始点,指定该点的刀轴矢量,以最小角度变化为原则规划相邻刀轴,遍历刀触点完成初始刀轴规划。单个刀触点的无干涉刀轴空间内可能存在多个刀轴矢量满足最小角度变化要求,因此初始刀轴轨迹存在多种可能。若刀轴轨迹具有较好的光顺性,其扫掠面积较小,因此可利用刀轴扫掠面积判断刀轨的光顺性。利用 ci、ti、ci+1、ti+1四点表示相邻刀轴,如图 5 所示。
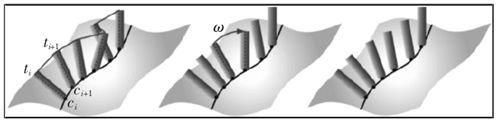
图5:刀轴光顺优化
相邻刀轴间的扫掠面积可近似表示为:
若刀轨共含有 N 个刀触点,则刀轨整体的扫掠面积可表示为:
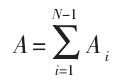
计算初始刀轴轨迹的扫掠面积,提取扫掠面积最小的刀轴轨迹。若结果不唯一,可根据角速度方差进一步对刀轴轨迹进行筛选。在相同的扫掠面积下,刀轴的角速度存在差异,光顺的刀轴轨迹应具备更小的角速度波动。因为相邻刀轴的间距极小,因此角速度可近似表示为:
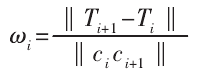
角速度的波动可用角速度方差表示:
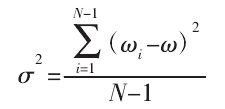
式中:ω—平均角速度,方差最小的刀轴轨迹具备更理想的光顺性。
4、验证实例
建立的工件模型,将工件表面离散为单位长度 1mm 的三角网格,提取网格节点(共计 8403 个)建立工件点云模型,如图 6 所示。利用 UG NX 软件生成刀轨曲线,按方法构建任一刀触点的无干涉刀轴空间。以刀位点(7.0283 24.4214 12.5602)为例,其无干涉刀轴空间,如图 7 所示。从该点的无干涉和干涉刀轴空间内分别选取刀轴矢量生成刀轨,在 UG 内对刀轨进行仿真分析,结果如图 8 所示。

图6:工件点云模型
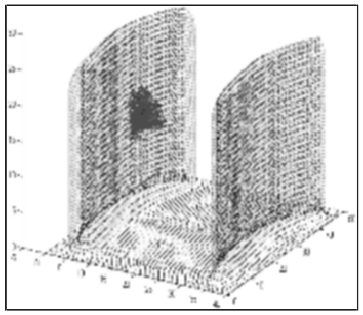
图7:无干涉刀轴空间
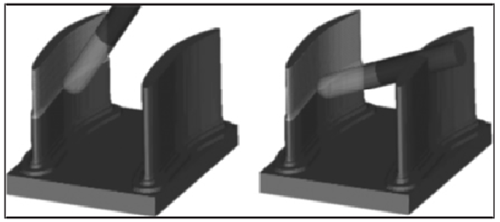
图8:无干涉和干涉刀轴仿真
仿真结果表明无干涉刀轴空间内的刀轴与工件表面存在明显间距,加工过程无干涉;干涉刀轴空间内的刀轴矢量使刀具侵入工件内部,该刀轴无法应用于实际加工。对干涉刀轴进行修正处理,并利用投影法优化修正过程,如图 9、图 10 所示。修正后的刀轴矢量可有效避免干涉,在投影法约束下,参与干涉检测的曲面离散点减少至 644 个,干涉检测量大幅减少。
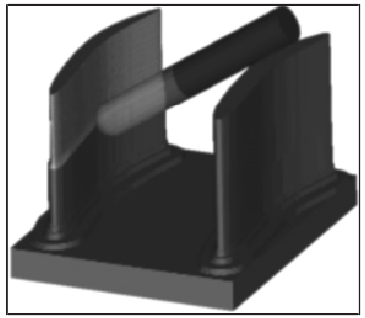
图9:修正刀轴仿真
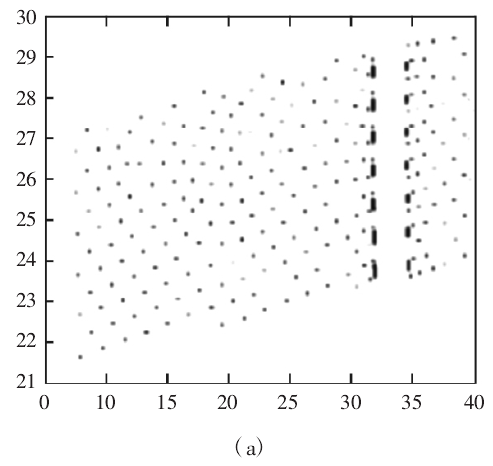
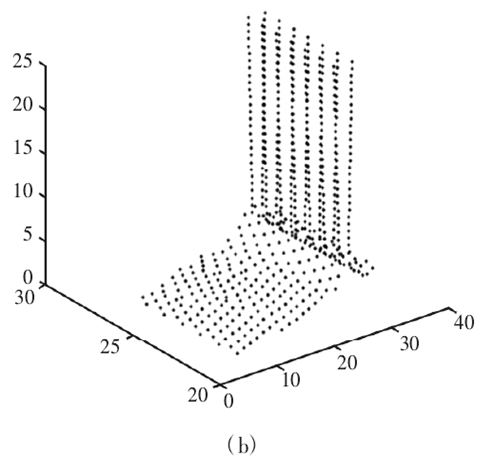
图10:刀具投影内的曲面离散点
利用五轴数控加工中心将修正后的无干涉刀轨应用于实际加工,如图 11 所示。

图11:加工结果
在实际加工中,刀杆与工件保持安全间距,加工过程稳定无干涉。由仿真结果可知相较于修正刀轴,无干涉刀轴与工件的间距更充裕,因此利用无干涉刀轴空间生成的刀轨亦可避免加工干涉。
5、结论
(1)利用方法生成的无干涉刀轴空间规划刀轴矢量可保证加工过程的可靠性,对原先干涉的刀轴矢量进行修正处理也可实现干涉避让;
(2)点云模型共有 8403 个曲面离散点,初始刀轴空间内包含离散点 6806 个,位于刀具投影内的曲面离散点为 644 个,投影法有效减少了参与干涉检测的曲面离散点数量,提高了计算效率。
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息





