基于灰关联的加工中心可用性需求重要度研究
2018-4-17 来源:转载 作者:孟书 申桂香 陈炳锟 孙曙光
摘要:为快速、准确地响应加工中心用户的可用性需求,需要准确评估加工中心各组件对用户可用性需求的满足程度,从而有针对性地构建可用性保障机制。针对加工中心产品的用户可用性需求的特点,以及加工中心各组件间自相关关系,引入质量功能展开理论(Qualityfunctiondeployment, QFD),建立可用性功能展开屋模型(Dynamic availability of the house, DHOA) 由于用户需求与加工中心各组件间的相关系数具有小确定性、呈区间数值的特点,采用区间灰关联分析与可用性功能展开融介方法,求解可用性功能展开模型的输出项,确定各组件对可用性需求重要度。以国产某型号加工中心为实例,验证该模型的合理性与有效性。
关键词:加工中心;DHOA模型;自相关性;区间灰关联分析
0、前言
数控机床作为现代化“工作母机”,是实现制造技术和装备制造业现代化的重要基础装备。而加工中心作为量大面广的数控机床代表性产品,其发展更是重中之重。
随着复合功能和密集型技术的引入,加工中心的不可靠因素和故障隐患增多,在运转和使用过程中故障发生概率增加、故障机理复杂,使得加工中心可用性基础技术的研究成为制约国内加工中心技术发展的主要瓶颈。维护机床“要用时就能用”的状态,提高其可用性水平是提高我国机床产业的市场竞争力的关键所在。
近年来,各学者对可用性的研究主要从以下几个方面展开:从产品故障发生机理入手,追踪故障原因,基于故障模式、影响及危害性分析(Failure mode effects and criticality analysis,FMECA)技术进行薄弱环节研究;根据产品故障事件发生的原因及传递性,基于GO法分析、故障树分析(Faulttree analysis, FTA)等进行故障分析研究;从产品的故障问隔时问及故障的维修时问,进行可靠度模型及维修度模型研究,进而获得固有可用度及瞬时可用度模型fl,该方法主要用于可用性评价的研究;通过产品各了部件与整机可靠性参数的函数关系,评价了部件发生故障对整机发生故障的贡献程度等。以上的研究主要是以产品本体在运行中暴露的障数据为基础,针对故障发生时问、维修时问、故障部位、故障原因或故障模式等从不同角度展开的研究。以上研究的成果仍不能满足广大机床用户对加工中心可用性的需求。
当前,用户导向的加工中心已经成为市场需求的趋势。在可用性研究中快速响应用户需求,将需求信息转化为加工中心关键组件的可用性改进方案,是当前提高加工中心可用性水平的有效方法。在此背景下,本文将以用户的可用性需求为驱动,结合加工中心的故障机理,综合进行可用性功能展开的研究。
根据前期研究发现,用户对加工中心可用性的需求多样化,对不同需求指标的重视程度不一,加工中心各组件对不同需求指标的影响程度也不同,以及加工中心各组件问存在相互影响的关系。为了综合考虑以上多个因素的影响,本文引入质量功能展开(Quality function deployment, QFD)理论,通过可用性功能展开及区问灰关联融合技术,研究加工中心各组件的可用性需求重要度的求解方法,并结合具体实例对该方法进行验证。
1、构建可用性功能展开模型
QFD是指产品从设计、生产等各项工作都是以顾客的具体需求为中心,把顾客的需求分解为具体可执行的各项具体措施,从而保证产品满足顾客的需求。
根据QFD理论,构建可用性功能展开屋模型(Dynamic availability of the house, DHOA)。如图1所示,该模型为房屋结构。其中,左墙为用户需求指标及其权重,是输入项之一;房问,加工中心组件与需求指标之问的相关关系矩阵,是输入项之二;屋顶为加工中心组件问白相关关系矩阵,是输入项之三;输出项,为综合考虑用户需求和加工中心各组件问自相关关系的可用性需求重要度。
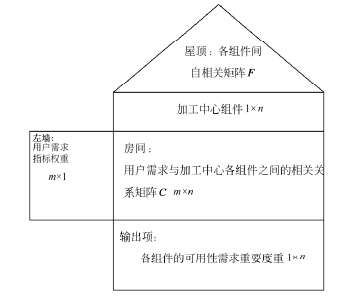
图1 加工中心可用性功能展开模型
通过以上模型,将用户需求与加工中心各组件联系在一起,找出影响可用性需求的重要组件,从而实现通过最少的可用性改进投入,最大程度满足用户需求。根据模型中多个输入项信息,以下将通过对可用性功能展开模型进行逐步计算,得到可用性屋的输出项矩阵,从而确定对用户整体需求的提升起关键作用的加工中心组件。为便于计算,本文首先对“左墙”与“房问”的相关关系矩阵进行分析,求出加工中心各组件可用性需求初始重要度;其次结合“屋顶”各组件问白相关矩阵,确定可用屋的最终输出项矩阵,即:加工中心各组件的可用性需求重要度。
2 、基于灰关联分析的初始重要度
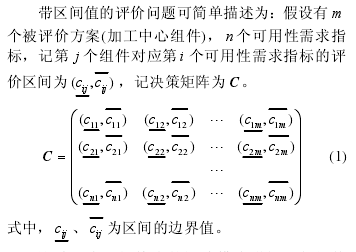
这种具有区间特点的矩阵模式增加了各组件的初始影响权重的获得难度,为解决这一难题,本节采用区间灰关联分析方法进行求解。
2.1 确定下界矩阵与上界矩阵

其中式(2)、(3)分别为下界矩阵与上界矩阵。
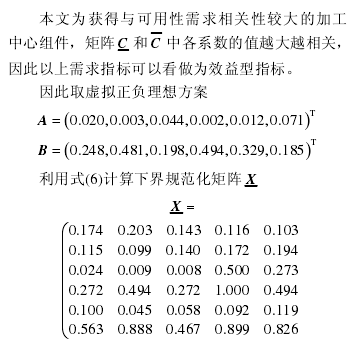
2.2 确定虚拟理想方案与负理想方案
2.2.1 对下界矩阵 C 取虚拟负理想方案

2.3 规范化处理
由于关联度计算数据的量纲可能不相同,一般情况不能直接计算关联系数,必将由量纲数据变为量纲一的数据。规范化处理方法如下。

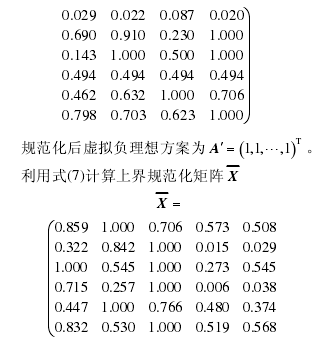
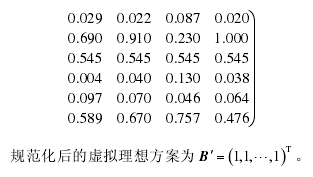
(2) 对上界矩阵,规范化公式如下。
对效益型指标

2.4 计算规范化后的上、下界矩阵与虚拟正负理想方案之间的关联度
2.4.1 计算规范化后的下界矩阵与虚拟理想方案的关联度

2.4.2 计算规范化后的上界矩阵与虚拟理想方案的关联度

2.5 加工中心初始重要度


式(12)称为灰色优选模型,且知当ju 越大时,第 j 个加工中心组件越接近虚拟理想方案,越远离虚拟负理想方案。ju 为加工中心组件相关关系的可用性需求初始重要度。
3、考虑自相关性的可用性需求重要度
加工中心复杂系统中各组件间存在相互影响关系,其相关关系主要体现在一个组件的故障导致另一个组件故障的发生,具有传递性。

组件间自相关矩阵在 DHOA 模型中体现在“屋顶”部分,见图 2。上三角形为前面的加工中心组件对后面组件的影响,如 F49是指加工中心组件 V影响组件 L 的相关系数;下三角形为后面组件对前面组件的影响,如 F94是指加工中心组件 L 影响组件 V 的相关系数。
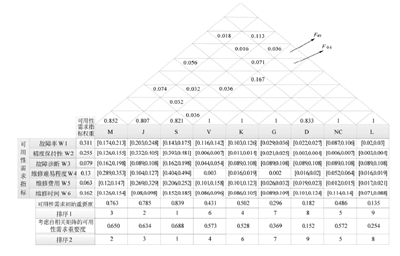
图2 加工中心可用性功能展开模型及输出项
考虑加工中心组件间的自相关关系后,各组件对可用性需求的贡献程度(各组件的可用性需求重要度)定义为ju ,该值可由式(13)进行计算
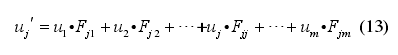
4、加工中心可用性功能展开实例分析
通过对加工中心特定用户调研,确定可用性需求指标及其代号如表 1 所示。
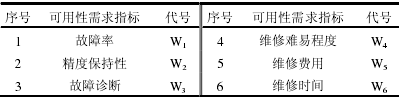
表1 可用性需求指标及代号
加工中心主要组件如表 2所示。
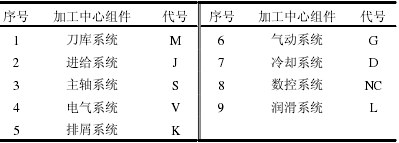
表2 加工中心组件及代号
4.1 加工中心组件可用性需求初始重要度
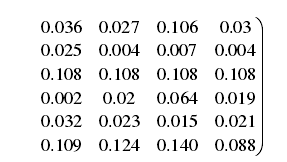
针对每一项可用性需求指标,根据加工中心各组件自身特点,彼此横向比较,确定其对每项需求指标的贡献百分比,从而构建相关关系矩阵 C,具体数据见图 2 的房间部分。
利用式(2)、(3)将 C 矩阵分为上、下界矩阵

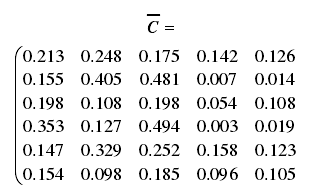
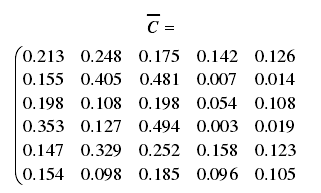
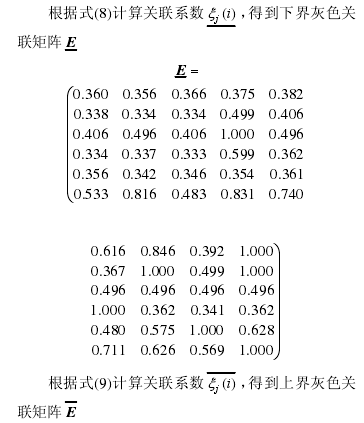
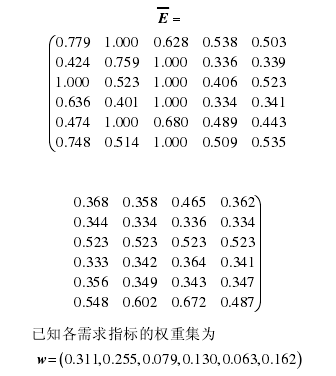

4.2 加工中心组件可用性需求重要度分析
通过加工中心组件故障原因的分析,确定独立故障及相关故障,并构建组件间自相关矩阵 F。数据见图 2从加工中心可用性功能展开的输出项中可看出,主轴系统的可用性需求重要度值最大,该组件对用户需求的响应最强烈,结合“房间”的相关关系矩阵,可看出主轴系统在精度保持性、维修难易程度及维修时间方面对用户需求的影响都是最严重的,因此经 DHOA 模型分析得出该组件对可用性需求影响最重要的结论,符合实际情况。
另外,考虑组件间自相关性后,主轴系统、进给系统、刀库系统的可用性需求重要度均有下降,从“屋顶”自相关关系矩阵中可看出,这些组件发生故障均有被其他组件影响的情况,因此其可用性需求重要度有所下降属正常现象。
通过构建 DHOA 模型进行用户需求驱动下的加工中心组件可用性需求重要度研究,不仅能够获得响应用户需求的最重要的组件,还能够从模型直观掌握需求信息与加工中心组件之间的关系及组件间的自相关关系的具体信息“屋顶”部分。

5、 结论
(1) 本文提出的 DHOA 模型,是以用户可用性需求为驱动,并结合加工中心组件间故障传递关系,展开的一种多输入项的综合分析技术。通过该模型输出项的求解,可得到加工中心组件的可用性需求重要度。针对输出得到的重要组件进行重点的可用性改进实施,将能够最大程度地满足用户的需求。
(2) 针对可用性功能展开模型中相关关系系数具有区间数的特点,本文采用区间灰关联分析方法进行计算求解,为信息具有不确定性的模型求解技术提供了一个解决方法。
(3) 本文的方法对金属切削类数控机床具有通用性,尤其是故障具有传递特点,以及较重视用户需求的可用性研究。
来源:吉林大学机械科学与工程学院 吉林大学管理学院 山东师范大学管理科学与工程学院
投稿箱:
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
如果您有机床行业、企业相关新闻稿件发表,或进行资讯合作,欢迎联系本网编辑部, 邮箱:skjcsc@vip.sina.com
更多相关信息





