摘要: 机床有限元分析可以准确预测机床的性能，缩短机床研发周期，且龙门式铣床具有行程大、占地面积小等优点，因此龙门铣床的结构设计受到了广泛关注。以微型移动龙门式铣床为研究对象，建立了其本体结构有限元模型，在具体工况下对其进行静力学分析，得到了其应力、位移云图和静刚度; 通过模态分析，得到其前十阶模态固有频率和主振型。找到了机床的薄弱环节，为该铣床结构优化提供了依据。
 
      关键词: 微型铣床; 有限元; 静力学; 模态分析
 
       0 引言
 
      在机床结构分析中，有限元分析是一种用于计算复杂结构且极为有效的数值分析方法，国内外学者在这方面做了大量的研究。Hung，Jui P． 等通过有限元仿真，研究了机床直线导轨在不同预载下对于整机动态特性的影响，验证了该有限元模型对机床动态特性预测的可靠性［1］。Yu，Lianqing 等通过建立合理的结合面模型以及整机有限元模型，研究了机床整机刚度［2］。殊海燕等通过有限元软件ANSYS 对数控立式机床做了静力学和模态分析，找到了机床薄弱环节［3］。赵兴玉利用有限元法对龙门铣床结构进行了静动态分析，研究了各部件对整机刚度的贡献，为其优化设计提供了理论依据［4］。
 
       龙门铣床具有刚性好，效率高，操作方便，结构简单，性能全面性等特点，且工作行程大，占地面积小，因此受到了广泛关注。文章以微型移动龙门式铣床为研究对象，对其本体结构进行了静动态特性的仿真，分析并找到了其结构中的薄弱环节，为该铣床的结构优化
提供了依据。
 
      1 、微型铣床本体结构
   
      该铣床床身材料采用45 钢，其外形尺寸为900mm ×700mm × 655mm，工作行程为500mm × 400mm ×150mm，主轴转速为0 ～ 15000r /min。其本体结构三维模型如图1 所示。
    
 
     
      图1 微型铣床本体结构
   
      2 、机床模态分析理论
 
      对于一台机床，可将其看做一个多自由度的线性系统，其基本振动平衡方程为［5-7］:[ M] X··( ) { } t + [ ] C X· { ( t)}+ [ K]{X( t)}= {F( t)} ( 1)式( 1) 中: [ M] 为质量矩阵，[ C] 为阻尼矩阵，[ K] 为刚度矩阵， X··{ ( t) }、X· { ( t) }和{X( t) }分别为加速度向量、速度向量和位移向量，{F( t) }为载荷向量。取载荷向量{F( t) }为0 值，得到系统在无阻尼状态下的自由振动方程:[ M] X··{ ( t)}+ [ K]{X( t)}= 0 ( 2)该铣床机构为弹性体，其自由振动可分解为一系列简谐振动叠加，式( 2) 方程的解可写为:{X( t)}= X0 { ( t)}sinωt ( 3)该铣床固有频率和振型的求解也就是( 2) 式方程的求解，其解如式( 3) 所示。

      3 、有限元模型的建立
 
      3． 1 有限元网格的划分
 
     综合考虑计算效率和精度，对该铣床几何模型进行适当简化，忽略进给电机及传动系统对本体结构的影响，主轴电机作为刚体，去除螺纹孔和部分倒角等细小特征［8］。各部件之间的结合部采用ABAQUS 中连接单元TIE 模拟。采用八节点六面体单元对机床本体进行网格划分，得到的有限元网格模型如图2 所示。

         
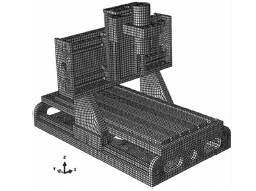
       图2 铣床本体有限元模型
 
       3． 2 静力学分析参数的确定
 
      根据铣削力经验公式有：
  
      
  
      4 、结果与分析
 
      4． 1 静力学分析
 
      在微型铣床刀具刀位点X、Y、Z 三个方向分别施加30． 6N 的力，同时在机床质点添加向下的重力加速度9800mm/s2，通过计算得到其静刚度如表1 所示，其位移和应力云图如图3 所示。
 

                                    表1 铣床位移和静刚度

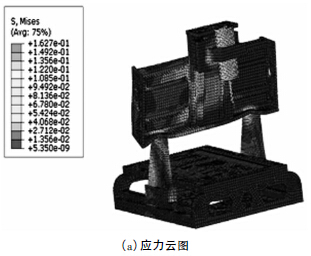
      图3 静力学分析应力、位移云图
    
      
  
     4． 2 模态分析
 
      采用ABAQUS 中的Lanczos 求解器提取了前10阶模态频率及其主振型，如表2 所示:
   
                              表2 微型铣床前十阶振型表

      由于篇幅有限只给出了前四阶振型图如图4 所示:

        
      图4 微型铣床前四阶振型图
   
     由表2 和图4 可知，机床前十阶的固有频率相差较大，机床整体有一定的抗震能力。工作台的变形影响到工件在加工中的精确位置，为机床重要的结构部件，前十阶的主振型有六阶为工作台的振动变形，且振动幅度相对较大，分析其原因为工作台动刚度不足。另外，由于立柱以上的床身扭振，引起刀具的摆动较大，对铣削精度影响较大，分析其原因为立柱与X 轴连接部分尺寸较小，从而造成连接部位刚度不足［9-10］。因此需要增大工作台本身的刚度以及立柱与X 轴床身连接部位的刚度，以求达到设计要求。
 
     5 总结
 
     文章通过对微型移动龙门式数控铣床进行静力学和模态分析，分析了其静刚度，找到了造成其结构刚度较弱的部位; 提取了其前十阶的固有频率和主振型，找到了其振动位移相对较大的部位，并分析了其原因，为该铣床进一步的结构分析和结构优化提供了参考依据。